一个静电问题的能量解释

项林川

（华中科技大学物理学院，湖北 武汉 430074）

一个静电问题的能量解释

项林川

（华中科技大学物理学院，湖北 武汉 430074）

本文从能量的角度讨论了一个静电问题.

能量；电荷分布；曲率；静电平衡

利用能量关系处理问题，思路简明，适用面宽，是一种在大学物理教学中值得重视的方法.

在一些大学物理教材和参考书中［1］，常以下面这个问题作为静电平衡时导体表面的电荷分布与曲率的关系的一个例子.如图1所示，用一根很长的细导线将两个半径分别为R1和R2的球形导体连接起来，并使这个导体系统带电，所带总电量为Q（＞0），求两导体球表面的电荷面密度σ1、σ2与曲率半径R1、R2的关系.

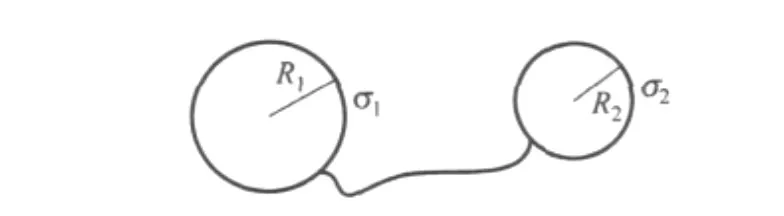
图1

这里要作一些适当的近似.因导线很长，可认为这两个导体球相距很远，每个球面上的电荷分布在另一球处所激发的电场可以忽略不计，故可把每个球近似地看作为孤立导体，在两导体球表面上的电荷分布各自都是均匀的；而细线上分布的少量电荷可以忽略不计.两导体球之间的细导线使得两球的电势相等，即［1］

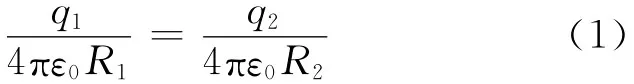
这是通常的解法.

下面我们从另外一个角度，即用能量的观点来重新考虑这个问题.

这两个导体球所组成的系统可看成是一个孤立系统，带电后很快就会达到静电平衡状态，这是系统的稳定状态，在该状态系统的能量最低.

因为两导体球相距很远，它们之间的相互作用可以忽略.因此，两球表面上的电荷分布各自都是均匀的，并且系统总的电场能量W 就等于两个导体球各自的电场能量的和，即

式中的W1和W2分别是第一和第二个导体球的电场能量.

对第一个球，由高斯定理［1］可知，球内部电场为零，球体外部电场沿径向朝外，大小为

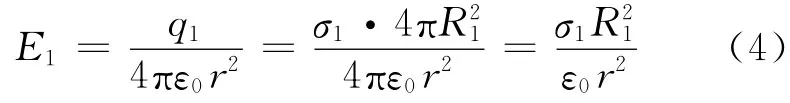
所以［1，2］，

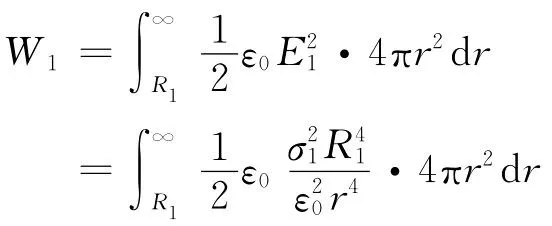
同理可得，

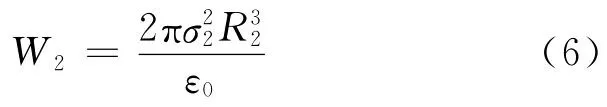
于是

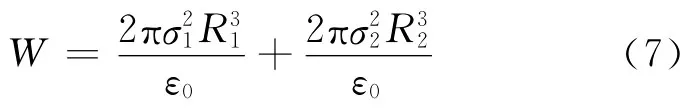
总电量Q显然满足下式

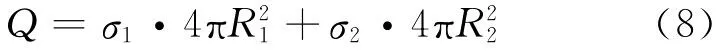
从式（7）和式（8）消去σ2可以得到

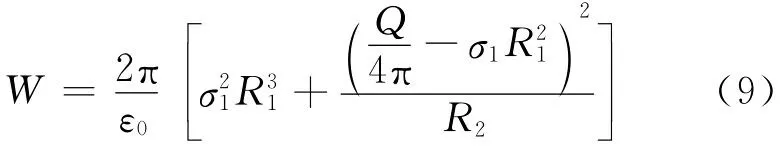
系统能量取最低值要求

将式（9）代入式（10），可得到

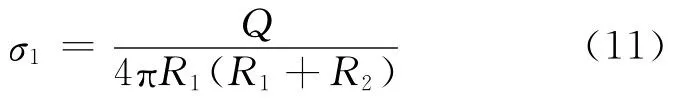
式（11）代入式（8）得

由式（11）、（12）得到

此即式（2）.

可见，从能量的角度得到了和前面同样的结论.虽然这个解法并不见得比第一种的解法来得简单，但却是运用能量关系求解问题的一个很好的例子.

［1］ 程守洙，江之永.普通物理学 第六版（上册）［M］.北京：高等教育出版社，2006

［2］ 邓顺蓉.大学物理［M］.武汉：湖北科学技术出版社，1998

ENERGY EXPLANATION FOR AN ELECTROSTATIC PROBLEM

Xiang Linchuan
（School of Physics，Huazhong University of Science and Technology，Wuhan，Hubei 430074）

In this paper，a discussion is given for an electrostatic problem from the point of view of energy.

energy；charge distribution；curvature；electrostatic equilibrium

2011－04－10）