塑料合金关于温度－频率－振幅的本构模型

陈希瑞，龚宪生

(1.重庆大学机械传动国家重点实验室，重庆400030;2.重庆大学机械工程学院，重庆400030; 3.重庆工商大学机械工程学院，重庆400067)

塑料合金关于温度－频率－振幅的本构模型

陈希瑞1，2，3，龚宪生1，2

(1.重庆大学机械传动国家重点实验室，重庆400030;2.重庆大学机械工程学院，重庆400030; 3.重庆工商大学机械工程学院，重庆400067)

以经典Kelvin分数导数理论为基础，建立新型BTG塑料合金的改进Kelvin分数导数动态本构模型，该模型综合描述了温度、频率和振幅与BTG塑料合金模量的关系.通过动态热分析仪DMA242，获取了BTG塑料合金几个温度下，振幅恒为30 μm时的频率扫描和几个频率下的恒温幅值扫描的动态存储模量和损耗模量实验数据.首先分析频率扫描实验数据，识别出各温度下的改进分数导数模型的系数，然后研究这些系数关于温度的变化规律，以此建立了温度频率模型.其次分析幅值扫描数据，发现不同频率的各实验振幅的模量与各自振幅30 μm的模量比值相等，所以建立了模量比值关于振幅的函数模型.将温度频率模型与模量比值振幅模型相乘就建立了综合考虑温度－频率－振幅的动态本构关系.建立的综合考虑温度－频率－振幅的本构模型能准确表达实验数据.结果表明：改进的综合考虑温度、频率和振幅的分数导数动态本构模型真确合理，该模型适合于BTG塑料合金的动态模量变化规律的描述.

塑料合金;存储模量;损耗模量;分数导数;本构模型

BTG塑料合金加工工艺性能好，具有良好的摩擦磨损性能和抗疲劳磨损性能，由此材料生产的弹性联轴器在使用中也表现出较好的隔振降噪功能.弹性联轴器工作环境复杂，其工作启停、速度变换频繁，工作频率范围大，工作环境温度不稳定，波动范围也较大，由于其承受的载荷不均匀，外载变化没规律，导致其工作时承载的外部载荷振幅频繁变化且变化幅值大.而BTG塑料合金具有非线性粘弹特性，其存储模量和损耗模量不是常数，大小会随着其工作频率、工作温度和工作振幅的变化而变化.为计算BTG塑料合金的联轴器在不同工作频率、温度和振幅下的强度或强度范围，建立能够准确描述BTG塑料合金的模量关于温度、频率和振幅变化规律的本构模型十分必要.

目前常用来描述粘弹材料本构模型的几种模型有标准流变学模型、分数阶导数模型、分数指数模型和微振子模型［1－10］，研究表明，不能说某一个模型更合理更科学，针对不同的材料需不同的模型来描述，即使是对材料实验数据采用同一模型，但采用不同的识别方法，得到的参数不同，其模型精度也不一样［1，4－6］.实际计算表明，这些模型也不一定能够同时准确表达模量和阻尼，甚至按存储模量的实验数据和模型识别的参数，对损耗模量的描述误差就很大，相反，按损耗模量的实验数据和模型识别的参数，对存储模量的描述误差也很大.在前期计算中表明，标准的流变机械模型对BTG的存储模量和损耗模量的变化趋势都不能准确描述.另一方面，这些模型只反应模量或阻尼随频率变化的规律，模型中并未考虑温度和振幅对它们的影响，而实际上它们受温度和振幅的影响都很大，所以必须对这些模型加以改进，建立能够同时反应温度、频率和振幅的本构模型.

本文利用动态实验仪器DMA242进行了几个温度下的频率扫描实验和几个频率下的幅值扫描实验，分析频率扫描实验数据，根据实验数据的分析，首先建立恒振幅下考虑温度的分数导数模型，再在此基础上考虑振幅的影响，最终建立综合考虑温度－频率－振幅的本构模型.

1 分数阶导数粘弹本构模型理论

单向拉伸应力－应变的分数阶粘弹性通用一般关系为［4－9］

对式(1)进行Fourier变换，得分数导数频域模型

由式(2)可得分数导数模型频域的复模量

其中

由式(3)可得，由一个弹簧和一个Abel粘壶［1，6］并联构成的Kelvin分数导数模型复模量为

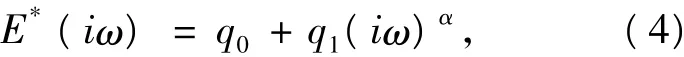
存储和损耗模量为

其中E'为存储模量，E″为损耗模量.

2 考虑温度－频率－振幅的分数导数模型建立及其参数识别

式(5)中表达的存储和损耗模量只有频率因素，未考虑温度振幅的因素，而实际上模量受温度振幅影响较大，因此根据式(5)并考虑实验频率单位为Hz，再加之按存储模量(或损耗模量)识别出的参数能精确表达存储模量(或损耗模量)，但不能精确表达损耗模量(或存储模量)，分别将考虑温度－频率－振幅的存储和损耗模量表达为［4］

图1为振幅30 μm时各温度下的频率扫描的存储模量和损耗模量实验数据，基于此先建立识别出振幅d=30 μm时的温度－频率模型，即

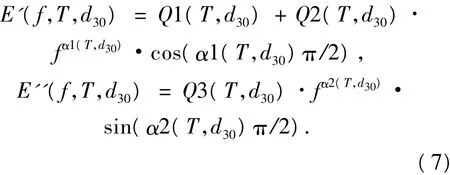
在不引起混淆情况下，下文公式图表中E'(f，T，d30)、E''(f，T，d30)、Q1(T，d30)、Q2(T，d30)、Q3(T，d30)、α1(T，d30)、α2(T，d30) 均 简 化 为 E'(f，T)、E''(f，T)、Q1(T)、Q2(T)、Q3(T)、α1(T)、α2(T).

根据图1实验数据和式(7)的模型，利用非线性最小二乘法识别出恒定振幅下温度变量Q 1(T)、Q2(T)、Q3(T)、α1(T)、α2(T)在各实验温度下的值，如表1所示.将各温度下的值代入模型绘制的模型拟合曲线如图1所示，各温度下的拟合曲线精确地表达了实验数据.这说明用分数导数模型来描述材料模量关于频率变化规律是合理的，不过模型的系数是温度的变化量，所以研究系数的温度变化规律很有必要.由表1数据及其图 2所示的 Q1(T)、Q2(T)、Q3(T)、α1(T)、α2(T)关于温度散点图的分布可以看出，Q1(T)、α1(T)、α2(T)数据点的分布为一条关于温度变量单调下降且凹的分布曲线，经计算Q1(T)、α1(T)、α2(T)分别用式(8)、(9)的表达式形式能分别对其识别值准确的拟合，Q2(T)、Q3(T)数据点的分布为关于温度变量单调上升且凸的分布曲线，经计算式(10)的表达形式能准确表达其识别数据.

根据表1各列数据及其相应温度变量模型，识别出的相应系数如表2所示，将相应系数代入各式绘制其模型拟合曲线如图2所示，各曲线与其相应识别值及变化趋势相当吻合.到此，将表2系数及式(8)、(9)和(10)代入式(7)，得出振幅d=30 μm时的温度－频率模型.

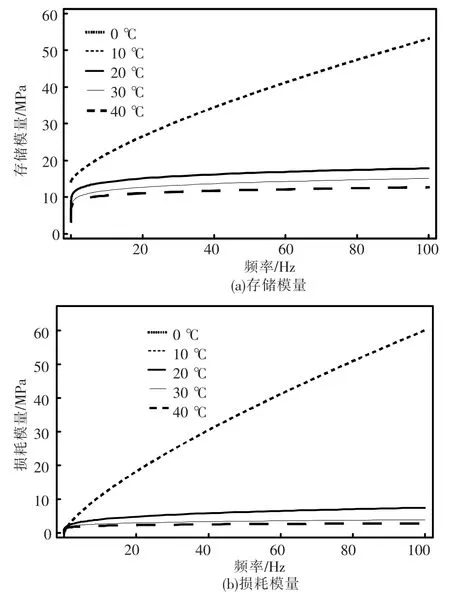
图1 振幅30 μm时各温度下频率扫描实验数据及模型拟合曲线

表1 温度变量Q1(T)、Q2(T)、Q3(T)、α1(T)和α2(T)在各实验温度下的识别值

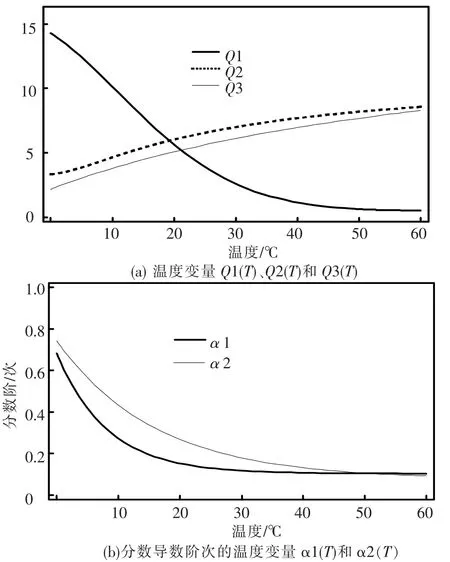
图2 温度变量识别值及其模型曲线

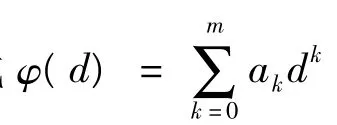
表2 温度变量Q1(T)、Q2(T)、Q3(T)、α1(T)和α2(T)模型的系数

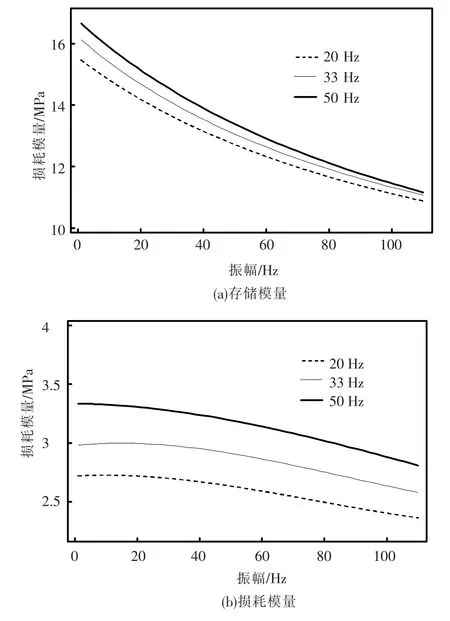
图3 各频率下振幅扫描的模量实验数据及其拟合曲线

基于此对振幅扫描实验数据进一步处理，由于各温度下的频率扫描是在恒振幅d=30 μm的工况下得到的，因此将振幅扫描的各振幅下的模量值除以振幅d=30 μm的模量值，存储模量和损耗模量比值分别记为E'A/E'30和E″A/E″30，其计算结果如表3所示.

从表3数据发现各频率下在相同振幅值时E'A/E'30(或 E″A/E″30)的值相等，也就是说E'A/E'30(或 E″A/E″30)的值与频率无关.分析如图4所示的E'A/E'30和E″A/E″30关于振幅的散点图可看出，散点数据分布为一条关于振幅变量单调下降且凹的分布曲线，经计算 E'A/E'30和E″A/E″30的值用式(11)的表达形式能准确表达其关于振幅的变化规律.

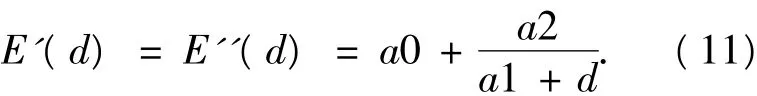
根据表3计算的E'A/E'30和 E″A/E″30的值，按模型式(11)识别出各自系数如表4所示.根据识别出的系数绘制的模型曲线如图4所示，表明模型式(11)能准确表达比值 E'A/E'30和 E″A/E″30关于振幅的变化规律及其趋势.通过上述的计算分析可知，式(7)表达的是振幅d=30 μm的任意温度频率的模量变化规律，而式(11)表达的是各振幅下的模量相对振幅d=30 μm的模量的倍数.由此两者相乘可得模量关于温度－频率－振幅的综合本构模型:

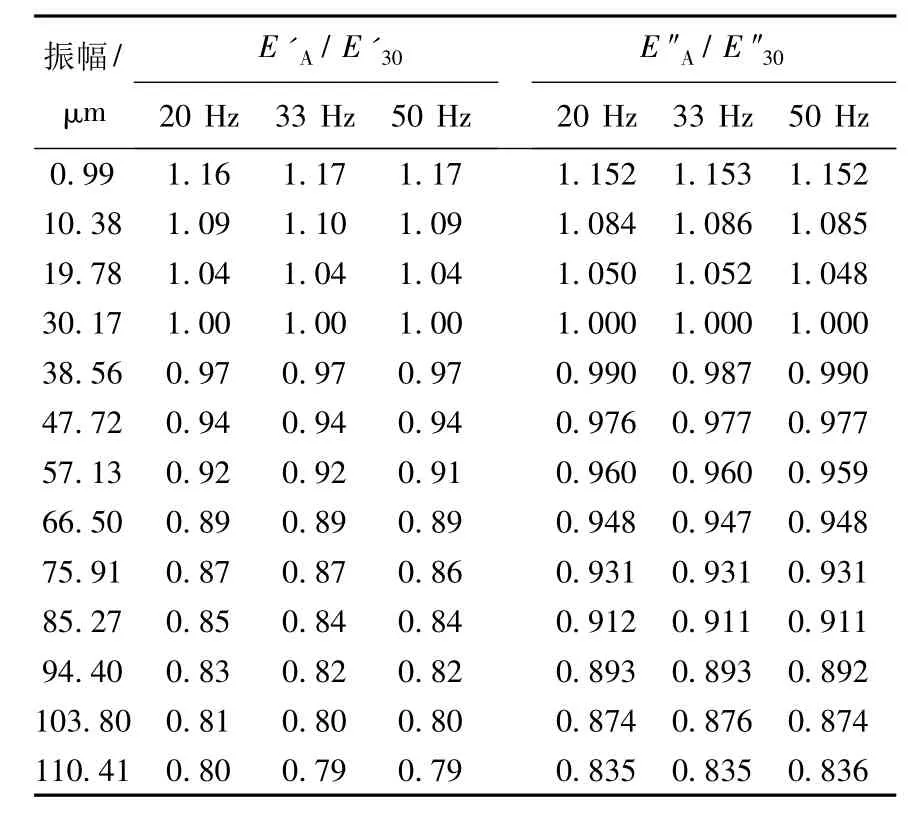
表3 各振幅模量E＇(")A 与振幅30μm时模量E＇(")30的比值

图4 E'A/E'30和E″A/E″30的计算值及其拟合曲线

表4 根据E'A/E'30和 E″A/E″30的比值识别的E'(d)、E''(d)的系数

3 讨论

为定量说明模型精度，定义存储模量和损耗模量的偏差为:

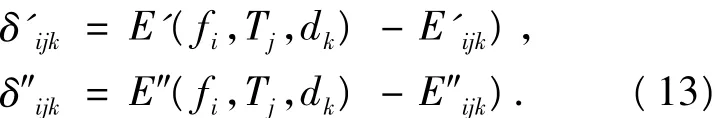
其中:δ'ijk、δ″ijk为在(fi，Tj，dk)点的偏差值;E'ijk、E″ijk为在(fi，Tj，dk)点的实验值;E'(fi，Tj，dk)、E″(fi，Tj，dk)为在(fi，Tj，dk)点的模型计算值.按上述定义，计算得偏差平方和、平均偏差平方和、均偏差、最大偏差和最大相对偏差见表5，计算结果表明，模型精度较高，能准确表达实验数据.

表5 存储模量和损耗模量基于偏差的统计计算

按经典的分数导数模型计算，式(6)中Q 3 (T)应等于Q2(T)，α2(T)应等于α1(T).但分别按存储模量和损耗模量的实验数据按式(6)模型计算结果表明Q3(T)不等于Q2(T)，α2(T)不等于α1(T).这就表明按存储模量数据及其模型识别的参数不能准确表达损耗模量，同样按损耗模量数据及其模型识别的参数不能准确表达存储模量，所以按传统分数导数计算得到的复模量E*=E'+iE″中E'和E″在数量上有一项不准确.而在应力应变的宏观计算中，E*=E'+iE″中每一项数量上准确很重要，所以将E'、E″看成各自相互独立的量，依据实验数据各自按式(6)的模型识别各自参数，以达到同时对存储模量和损耗模量的准确描述的建模方法在宏观上是合理.

4 结论

1)对传统经典的Kelvin分数导数模型进行改进，分别建立了存储模量和损耗模量的模型，所建立模型均能准确表达存储模量和损耗模量的实验数据及其数据变化趋势，因此与经典Kelvin分数导数模型相比，使存储模量和损耗模量在数量上得到了准确的表达.

2)经典的Kelvin分数导数模尽管不能在数量上同时完全精确表达存储模量和损耗模量，也即是说由一个弹簧和一个服从分数导数的Abel粘壶并联构成的Kelvin分数导数的物理模型还不能完全准确反映BTG塑料合金动态力学物理特性，但都准确的表达了存储模量和损耗模量的变化趋势.由此可以断定分数导数的Abel粘壶反映了BTG塑料合金的粘性本质特征.

3)结合上述两点结论可以断定，应用多个A-bel粘壶和弹簧，采取合理的结构形式，就可能建立能完全准确反映BTG塑料合金动态力学的物理模型，有待进一步研究.

［1］林松，高庆，李映辉，等.一种考虑宽温宽频宽动态位移的粘弹性本构模型［J］.航空动力学报，2007，22 (3):431－438.

［2］郑健龙，钱国平，应荣华.沥青混合料热粘弹性本构关系试验测定及其力学应用［J］.工程力学，2008，25 (1):34－42.

［3］高庆，林松，杨显杰.丁基橡胶粘弹性材料的非线性蠕变本构描述［J］.应用力学学报，2007，24(3):386－391.

［4］林松，杨显杰，高庆，等.宽温宽频宽动态位移下ZN－33材料的黏弹行为［J］.宇航材料工艺，2007，(3):74－80.

［5］刘林超，张卫.服从分数代数Maxwell本构模型的粘弹阻尼材料性能分析［J］.材料科学与工程学报，2004，22(6):860－862.

［6孙海忠，张卫.服从分数导数Kelvin本构模型的粘弹性阻尼器的阻尼性能分析及试验研究［J］.振动工程学报，2008，21(1):40－45.

［7］刘岩，王忠金，宋辉，等.VPF粘性介质粘弹性本构关系研究［J］.材料科学与工艺，2008，16(2):176－180.

［8］周光泉，刘孝敏.粘弹性理论［M］.安徽:中国科学技术大学出版社，1996.

［9］龚元明，孙志杰，贺成红，等.不同预载/动载下纤维增强环氧树脂复合材料动态粘弹特性［J］.复合材料学报，2006，23(1):26－30.

［10］NIELSEN L E.高分子和复合材料的力学性能［M］.北京:轻工业出版社，1997.

Dynamic constitutive model related to temperature，frequency and amplitude for BTG plastic alloy

CHEN Xi-rui1，2，3，GONG Xian-sheng1，2
(1.The State Key Laboratory of Mechanical Transmission，Chongqing University，Chongqing 400030，China;2.College of Mechanical Engineering，Chongqing University，Chongqing 400030，China;3.College of Mechanical Engineering，Chongqing Technology and Business University，Chongqing 400067，China)

We established dynamic model of modified Kelvin fractional derivative for a new type of plastic alloy BTG based on the classical Kelvin fractional derivative theory.This model describes the modulus of plastic alloy BTG affected by temperature，frequency and amplitude.The experimental data of the storage modulus and loss modulus of the frequency sweep under conditions of constant amplitude 30 μm for several temperatures and amplitude scanning under conditions of constant temperature for several frequency were obtained first，and then the temperature-frequency model and the function model of modulus ratio about amplitude was set up，finally，the dynamic constitutive model about the temperature，frequency and amplitude was presented by the product of temperature-frequency model and function model of modulus ratio.The results show that the dynamic model of modified Kelvin fractional derivative is true and suitable to express the dynamic modulus of plastic alloy BTG.

plastic alloy;storage modulus;loss modulus;fractional derivative;constitutive model

TB302.3;TB332 文献标志码：A 文章编号：1005－0299(2011)05－0120－05

2010－08－09.

重庆市科技攻关计划项目(CSTC，2007AC3015);重庆大学机械传动国家重点实验室自主研究基金项目(0301002109137);重庆工商大学青年科研基金资助项目(0752008).

陈希瑞(1974－)，男，博士;

龚宪生(1956－)，男，教授，博士生导师.

龚宪生，E-mail:chxirui@126.com.

(编辑 程利冬)