7维稳定耗散LV系统性质初探*

张建钢

(浙江师范大学数理与信息工程学院，浙江金华 321004)

0 引言

Lotka-Volterra系统(LV系统)是指下面的常微分方程组:

式(1)中:xi表示第i个物种的种群密度;aij表示种间作用系数;λi是与环境相关的参数．这类系统广泛存在于物理、力学、化学、工程及社会经济等领域．

由于方程的动力学性质与作用矩阵A=(aij)n×n的代数性质密切相关，因此，根据矩阵A的特点，通常将LV系统分为3类:互利合作型(或相互竞争型)、保守型及耗散型．

前两类系统已被大量研究，耗散型系统尤其是稳定耗散系统的研究则相对较少．文献［1］对3维稳定耗散系统的充要条件作了分析;文献［2］对3维实耗散矩阵的充要条件作了详尽的探讨．一般性判断一个矩阵是否为稳定耗散有相当的难度，通过分类限定条件分析稳定耗散矩阵A的条件不失为一种有效的方法．例如，文献［3］用图表示LV系统，不同的作用矩阵可以唯一地对应一个图，对作用矩阵A所表示的图G(A)进行分类是合理的．鉴于此，文献［4］进一步讨论了稳定耗散矩阵的判定问题，并提出了最大稳定耗散图的概念，对5维系统进行了拓扑分类及动力学研究．文献［5］对4维稳定耗散系统的代数条件进行了充分研究;文献［6］对6维最大稳定耗散系统作了拓扑分类及动力学研究．本文对7维稳定耗散系统进行拓扑分类，结合耗散图的特点，按大类分析了系统最大稳定耗散的代数条件，并选择2类系统进行动力学性质剖析．

1 预备知识

为便于讨论，先介绍一些基本概念．

定义1［3］若存在正定对角阵D＞0，使得AD+DAT是半负定的，则称矩阵A是耗散的．

注1 定义1中的AD+DAT可由DA+ATD替代．2种定义是等价的［7］．

定义2［3］若矩阵A与˜A中的元素满足˜ajk=0⇔ajk=0，则称˜A为A的一个扰动．

若作用矩阵是耗散的(稳定耗散的)，则称对应的LV系统(1)是耗散的(稳定耗散的)．

文献［3］按这样的规则引进作用矩阵A的图形表示G(A):G(A)共有n个顶点，若aij≠0或aji≠0(i≠j)，则顶点i和j之间有边相连;若aii=0，则顶点i用◦表示;若aii≠0，则顶点i用·表示．

定义4［4］设G(A)为作用矩阵A的表示图，若A是稳定耗散的，但A^不是稳定耗散的(A^是指G(A)添加任意一条或几条边得到的图所对应的任意一个矩阵)，则称G(A)为最大稳定耗散图．

对于耗散的矩阵，不难验证aii≤0，(i=1，2，…，n)．关于稳定耗散矩阵，有下面结论:

命题2［7］若A为稳定耗散矩阵，i与j为G(A)相邻的2个点，则aiiajj＞aijaji．

命题3［7］若A为稳定耗散矩阵，则G(A)中的每个圈至少有一个满足aii＜0，ajj＜0的强连接［i，j］．

命题 4［4］若 ajj＜0(j=1，2，…，n)，则 A∈SD当且仅当存在 D=diag(d1，d2，…，dn)＞0，使得 DA ＜0．

命题5［4］若所有的aii=0，或某个akk＜0，且对所有i≠k有aii=0，则A∈SD当且仅当:1)G(A)是无圈的;2)aij≠0⇒aijaji＜0．

命题6［4］若不止一个 aii＜0，不失一般性，假设 aii＜0(i≤k)及 ajj=0(j＞ k)，M=(aij)(1≤i，j≤示G(A)中删除同时满足i≤k和j≤k的连接［i，j］后所得的图，则A∈SD当且仅是无圈的;2)∃diag(d1，d2，…，dn)＞0，使得D0M ＜0，diaij+djaji=0对一切i＞k或j＞k成立．其中，D0=diag(d1，d2，…，dk)．

2 主要结果

2．1 7维最大稳定耗散图的分类

根据稳定耗散矩阵的上述性质及最大稳定耗散图的定义，经过筛选可得定理1(鉴于篇幅所限，不再给出相应的图)．

定理1 对所有7×7稳定耗散矩阵，正好对应229种不同拓扑结构的最大稳定耗散图．

2．2 稳定耗散矩阵的代数条件

结合定理1的分类结果，下面分4大类讨论矩阵成为稳定耗散的充要条件．

第1大类，不含黑点或只含1个黑点的图(共59种)．运用命题4，易得定理2．

定理2 在所有7维最大稳定耗散图中，对不含黑点或只含1个黑点的图G(A)，对应的作用矩阵是稳定耗散的充要条件是:∀i≠j，aij≠0⇒aijaji＜0．

第2大类，只含2个黑点的图(共79种)．此处仅以图1为例给出结论，针对其他情形，除下标及形式稍加变化外，结论都与此相类似．

图1 7维最大稳定耗散图中仅含2个黑点的例图

定理3 对图1所示的只含2个黑点的图G(A)对应的作用矩阵A是稳定耗散的充要条件是:

3)当 a12a21=0时，有

当式(2)或式(3)满足时，都有

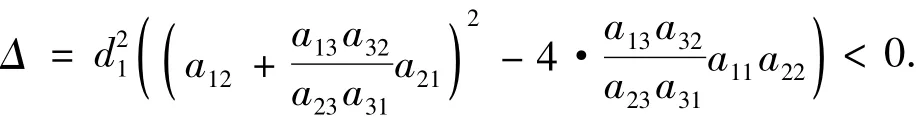
又由于d1a11＜0，于是xDAxT≤0恒成立，也即有x(DA+ATD)xT=2xDAxT≤0恒成立．因此，A为耗散矩阵．对A任意充分小的扰动˜A同样满足定理3中的3个条件，于是˜A也为耗散矩阵，因此A∈SD．

必要性 由图1可知，a11≠0，a22≠0，a33=a44=… =a77=0;同时，根据 A是耗散的知，a11≤0，a22≤0，因此 a11＜0，a22＜0．由于 A∈SD，故由命题 2 可得 a13a31＜0，…，a54a45＜0．因此，1)成立．由于 A是耗散的，故可找到 D=diag(d1，d2，…，d7)＞0，使得对∀x∈R7，有 xDAxT≤0，即

于是，令 x=(0，0，0，x4，1，0，0)，得(d4a45+d5a54)x4≤0 对一切 x4都成立．此时，d4a45+d5a54=0．再分别令 x=(0，0，0，0，x5，1，0)，x=(0，0，0，0，0，x6，1)，x=(1，0，0，0，0，0，x7)，x=(1，0，x3，0，0，0，0)，x=(0，1，x3，0，0，0，0)，得 d5a56+d6a65=0，d6a67+d7a76=0，d1a17+d7a71=0，d2a23+d3a32=0，d1a13+d3a31=0．因此，

第3大类，只含3个黑点的图(共58种)．此处仅以图2为例给出结论，针对其他情形，除下标及形式稍加变化外，结论都与此相类似．

图2 7维最大稳定耗散图中仅含3个黑点的例图

定理4 对图2所示的只含3个黑点的图G(A)，对应的作用矩阵A是稳定耗散的充要条件是:

必要性 由图2及命题2，易证1)成立．根据命题6，∃D=diag(d1，d2…，d7)＞0，使得 D0M ＜0，diaij+djaji=0 对一切 i＞3 或 j＞3 成立．其中 D0=diag(d1，d2，d3)．于是

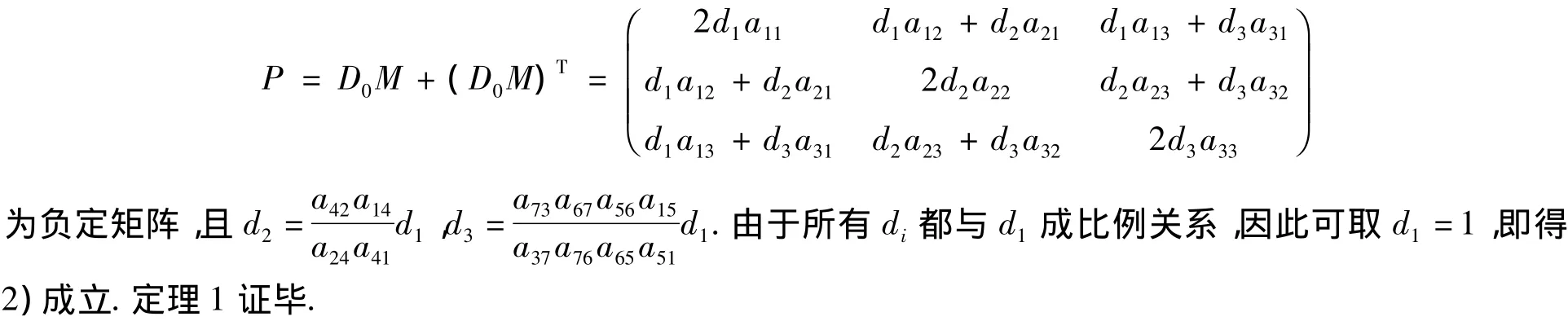
注2 只含4，5，6个黑点的情形共有32种拓扑结构，这些系统都有与定理4类似的结论．

第4大类，全为黑点的图(共1种)．

定理5 在所有7维稳定耗散图中，对全为黑点的图G(A)，对应的作用矩阵A是稳定耗散的充要条件是:

1)aii＜0，i=1，2，…，7;

2)∃D=diag(d1，d2，…，d7)＞0，使得 D*A*＜0，D*B*＜0，其中 D*，A*，B*分别为将 D，A，B 删除最后一行与最后一列后所得到的矩阵，B=A-1．

证明 结合命题4及文献［7］中的定理2，容易证得本结论．

2．3 稳定耗散矩阵的动力学性质

下面讨论7维稳定耗散系统的动力学性质．由于种类太多，本文仅讨论全白点图的情况，如图3所示，将它们所对应的LV系统分别标记为S(1)，S(2)，…，S(11)．

图3 7维最大稳定耗散图(全白点情形)

为此，假定系统有正平衡点q=(q1，q2，…，q7)，于是系统(1)可表述为

由于图3中的各个图的顶点均为白点，故aii=0(i=1，2，…，7)．又由于图3具备树型结构，故运用定理1及文献［8］的命题2．1可知它们对应的系统也是保守系统．因此，存在D=diag(d1，d2，…，d7)＞AD为反对称矩阵．本文假设系统已经作了上述尺度变换．

针对以上系统，选择S(11)，S(9)进行研究．

定理6 系统S(11)存在1个过点q的2维不变子流形，它被系统的周期轨充满;系统S(9)存在2个过点q的2维不变子流形，每个子流形被系统的周期轨充满．

证明 设作用矩阵A为反对称矩阵．系统S(11)的方程为

平衡点q处的线性化矩阵为

经计算得特征值为:

因为a21i＞0，qi＞0，所以λ6，λ7为一对共轭纯虚根．由Lyapunov次中心稳定性定理可知，系统 S(11)存在过q的2维不变子流形，它被系统的周期轨充满．

系统S(9)的方程为

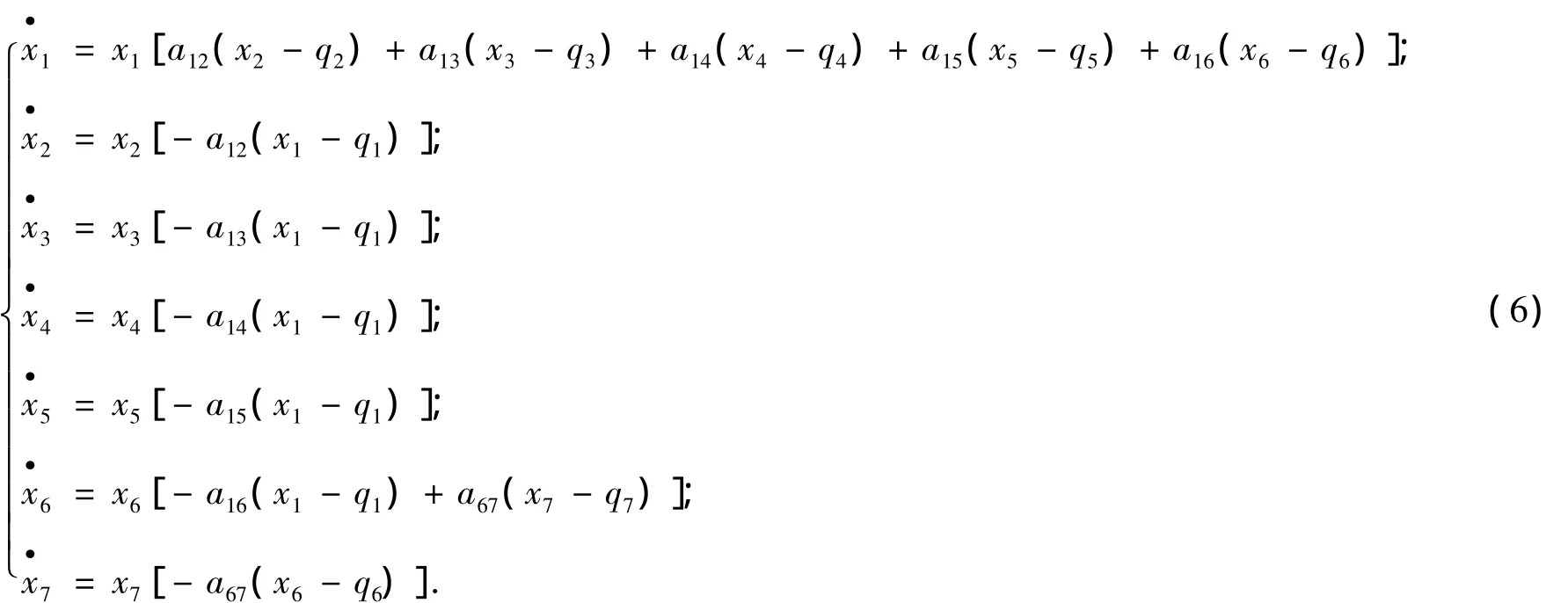
平衡点q处的线性化矩阵为

经计算得特征值为:

其中:

因此λ4，λ5为一对共轭纯虚根，λ6，λ7为一对共轭纯虚根．由Lyapunov次中心稳定性定理可知，系统S(9)存在2个过q的2维不变子流形，每个子流形被系统的周期轨充满．

［1］Cross G W．Three types of matrix stability［J］．Linear Algebra and Its Applications，1978，20(3):253-263．

［2］郭志明，周之铭，王寿松．3 ×3 实矩阵的 Volterra乘子［J］．数学的实践与认识，1995，25(1):47-54．

［3］Redheffer R，Zhou Zhiming．Global asymptotic stability for a class of many-variable Volterra prey-predator systems［J］．Nonl Anal T M A，1981，5(12):1309-1329．

［4］Zhao Xiaohua，Luo Jigui．Classification and dynamics of stably dissipative Lotka-Volterra systems［J］．International Journal of Non-Linear Mechanics，2010，45(6):603-607．

［5］戴灿华．四阶稳定耗散Lotka-Volterra系统的分类和动力学性质［D］．金华:浙江师范大学数理与信息工程学院，2010．

［6］陈莉莉．Lotka-Volterra系统及相关推广系统的耗散性及动力学［D］．金华:浙江师范大学数理与信息工程学院，2009．

［7］Redheffer R．Volterra multipliers Ⅱ［J］．SIAM J Alg Disc Math，1985，6(4):612-623．

［8］Duarte P，Fernandes R L，Oliva W M．Dynamics of the attractor in the Lotka-Volterra equations［J］．Journal of Differential Equations，1998，149(1):143-189．