用径向基函数解偏微分方程

张颖超

（广西师范大学数学科学学院，中国桂林 541004）

用径向基函数解偏微分方程

张颖超*

（广西师范大学数学科学学院，中国桂林 541004）

讨论了用正定径向基函数解偏微分方程，通过一个数值算例，说明这个方法是可行的．针对数值算例，比较了在相同步长时，不同的正定径向基函数对微分方程数值解的精确程度，并比较不同的正定径向基函数在相同的形状参数时绝对误差的差异，说明微分方程数值解的精确程度与径向基函数形状参数的取值密切相关．同时也论证了在插值过程中所得到的矩阵方程解的存在唯一性．

径向基函数;数值解;偏微分方程;线性无关

一般地，许多物理现象和工程技术问题都可以归结为一个微分方程．微分方程的解析解可以通过分离变量法和积分变换法等方法得到．微分方程的数值逼近可以通过Euler法，Runge-Kutta法和数值积分等方法得到［1-2］．近几十年来，人们的主要目标是寻找各种各样的无网格方法，利用径向基函数（RBF）解微分方程是受到普遍关注的无网格方法．1971年，Hardy［3］总结评论了关于multiquadric（MQ）函数的各种应用，特别是在地理，遥感，信号系统等方面的成功应用．自从Kansa［4-5］用径向基函数解偏微分方程（PDE），得到非常精确的解后，用径向基函数解偏微分方程引起越来越多的关注，并且Madych和Nelson［3，6-7］证实了MQ函数插值的收敛性．

近10年来，用径向基函数配置法解偏微分方程受到广泛关注，人们已经用径向基函数配置法解线性和非线性的偏微分方程［8-11］，有的用径向基函数配置法逼近椭圆型偏微分方程数值解［12-13］，并且取得了不错的结果，但是在逼近过程中所得到矩阵方程的系数矩阵是否可逆还没有被验证，即，数值解的唯一性还没有被验证．

本文主要讨论用正定径向基函数［14］解偏微分方程

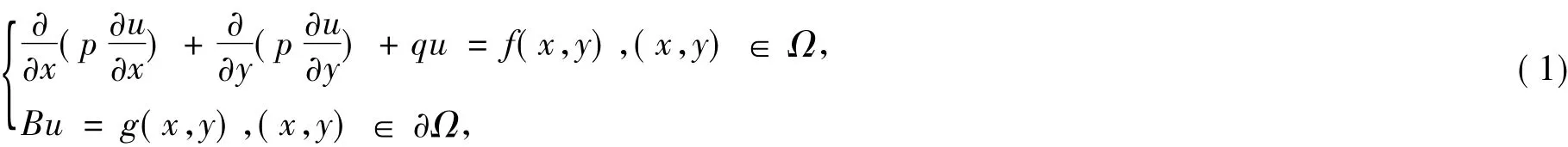
以下是常用的正定径向基函数．

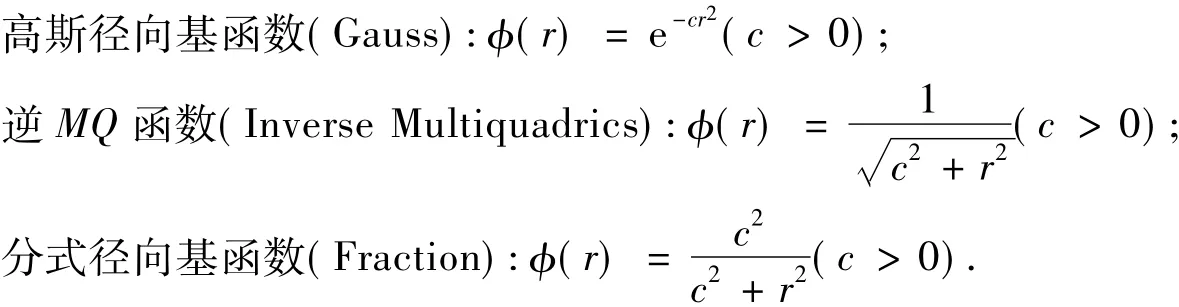
1 正定径向函数的应用

1．1 相关定理

对于任意阶可微函数u（r），r∈Ω⊂Rn，在Ω内配置N个散乱的数据点r1，r2，…，rN，令

其中λ1，λ2，…，λN是待定系数，φ（‖r－rj‖）（j=1，2，…）是正定径向基函数，‖·‖是欧几里得范数．本文取n=2，即r=（x，y）．

引理1［14］函数Φ（x）=φ（‖x‖）是正定函数的充分必要条件是Φ（x）的傅里叶变换几乎处处大于零．引理2［15］若F［Φ（x）］是Φ（x）的傅立叶变换，那么F［Φ″（x）］=（iω）2F［Φ（x）］．考虑正定径向基函数φ（‖r－rj‖）（j=1，2，…），设

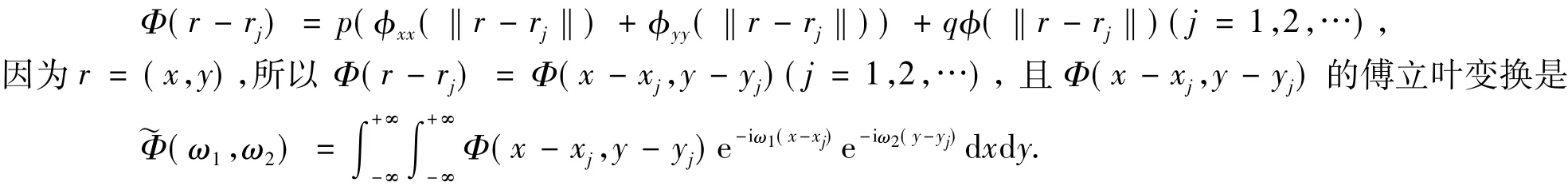
定理1若Φ（x－xj，y－yj）的傅立叶变换是证根据傅立叶变换的性质

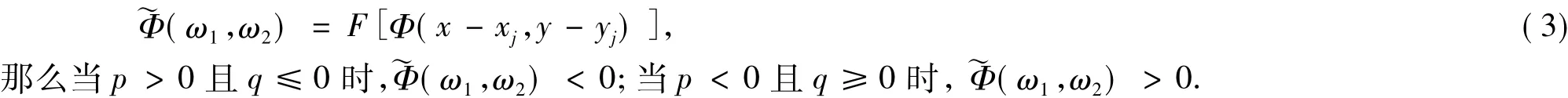
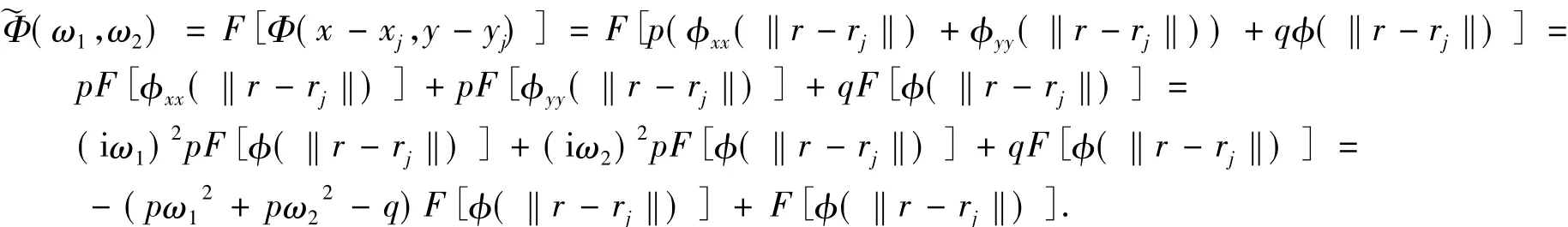
因为φ（‖r－rj‖）（j=1，2，…）是正定径向基函数，根据引理1，

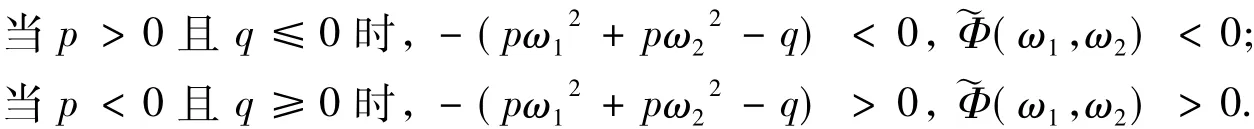
定理2当p＞0且q≤0，Φ（r－r1），Φ（r－r2），…，Φ（r－rN），…线性无关．

因此λj=0，1≤j≤N，所以假设不成立．所以Φ（r－r1），Φ（r－r2），…，Φ（r－rN），…线性无关．

1．2 方法分析

考虑偏微分方程

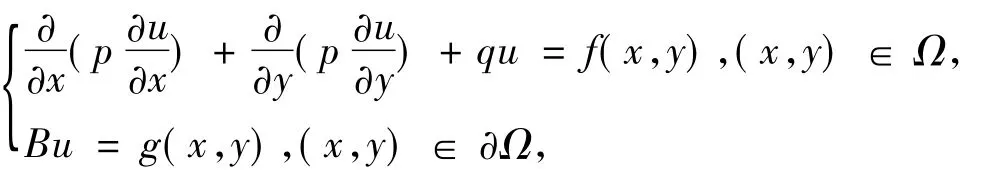
其中p＞0，q≤0或者p＜0，q≥0，Ω⊂R2，f（x，y），g（x，y）是连续函数，B是边界算子．在Ω内配置N个离散的数据点r1，r2，…，rN，其中r1，r2，…，rL是内部节点，rL+1，rL+2，…，rN是外部节点．设方程（1）的数值解为

其中λ1，λ2，…，λN为待定系数．由（1）式和（5）式得

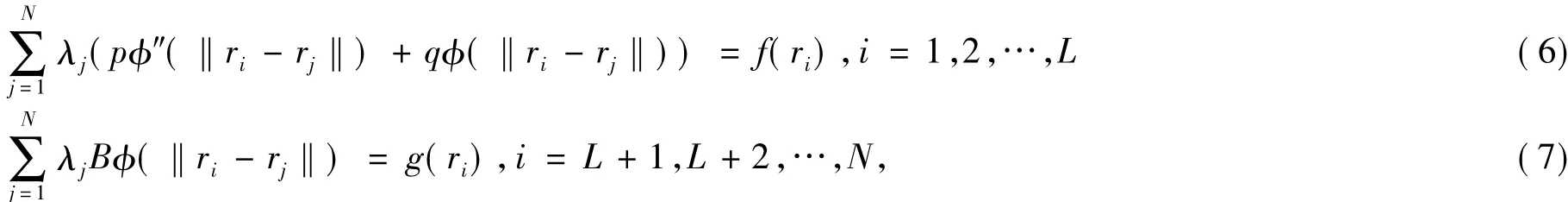
由（6）式，（7）式得到矩阵方程

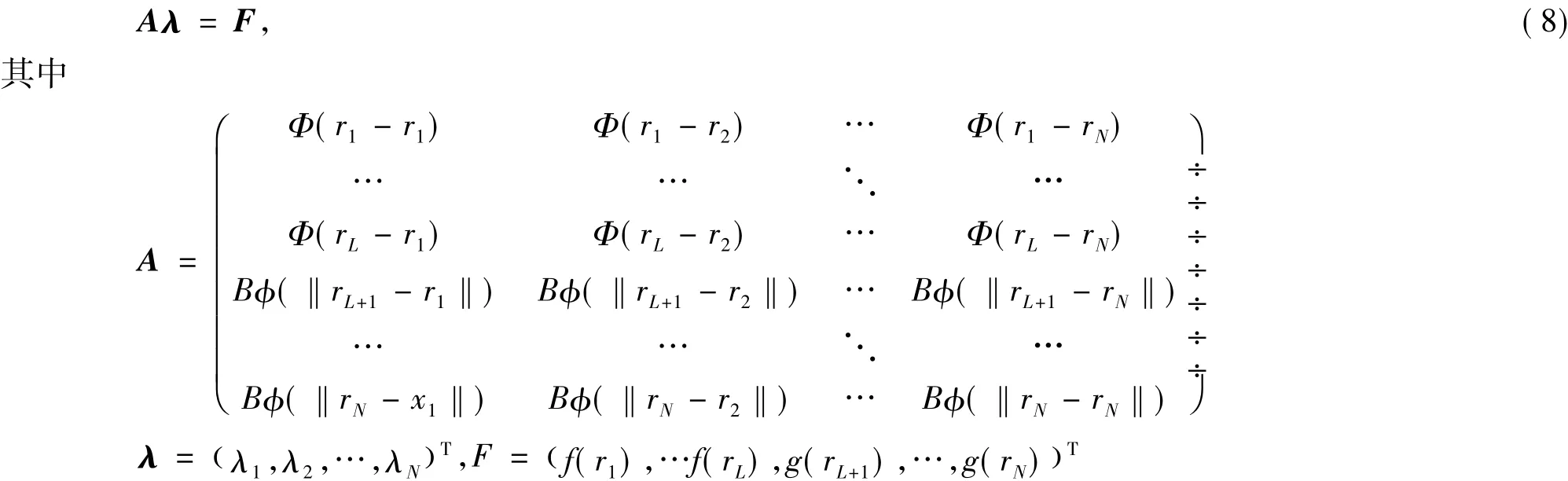
由定理2知，矩阵方程（8）的系数矩阵是非奇异的，所以矩阵方程有唯一解，只要从（8）式中解出λ，就可以得到方程（1）的近似解

2 数值算例

在这一部分，我们将通过一个数值算例来讨论正定径向基函数解常微分方程，用绝对误差描述数值解与精确解的差别．绝对误差的形式如下

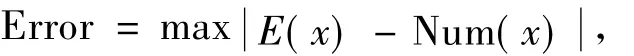
其中E（x）是精确解，Num（x）是数值解．

例已知偏微分方程

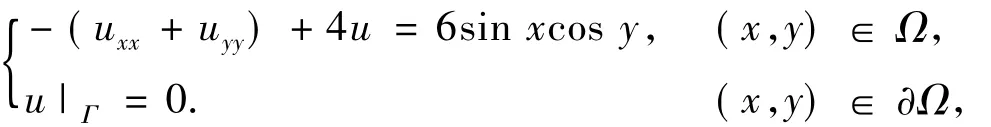
下面利用径向基函数配置法对上述微分方程求数值解，把区域Ω等分，步长，分别选用φ（r）= e－cr2（c＞0，为形状参数）和，为形状参数）作为基函数，所得数值解与精确解的绝对误差结果如表1和表2．

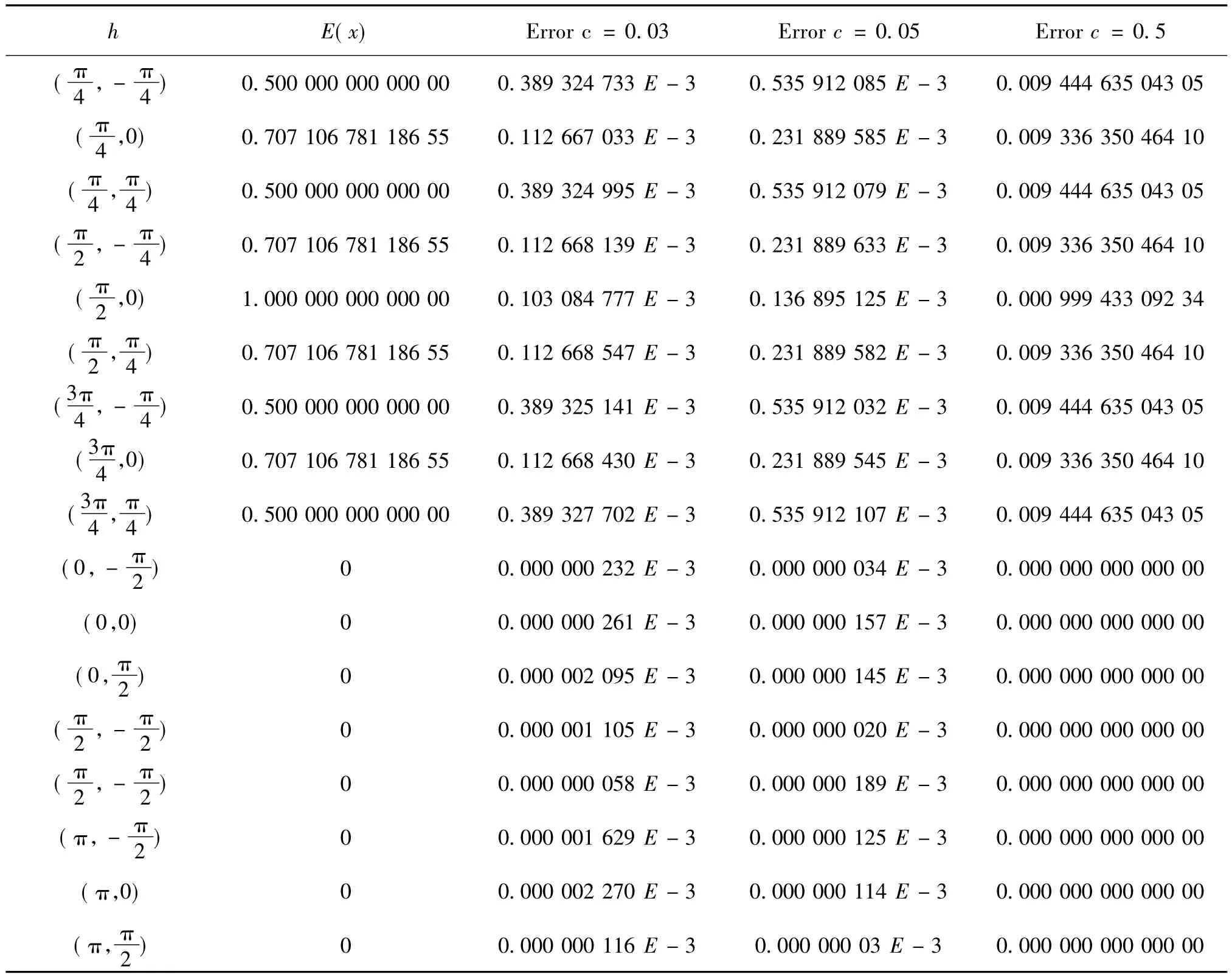
表1 φ（r）=e－cr2为基函数，不同形状参数时的绝对误差的比较

表2 为基函数，不同形状参数时的绝对误差

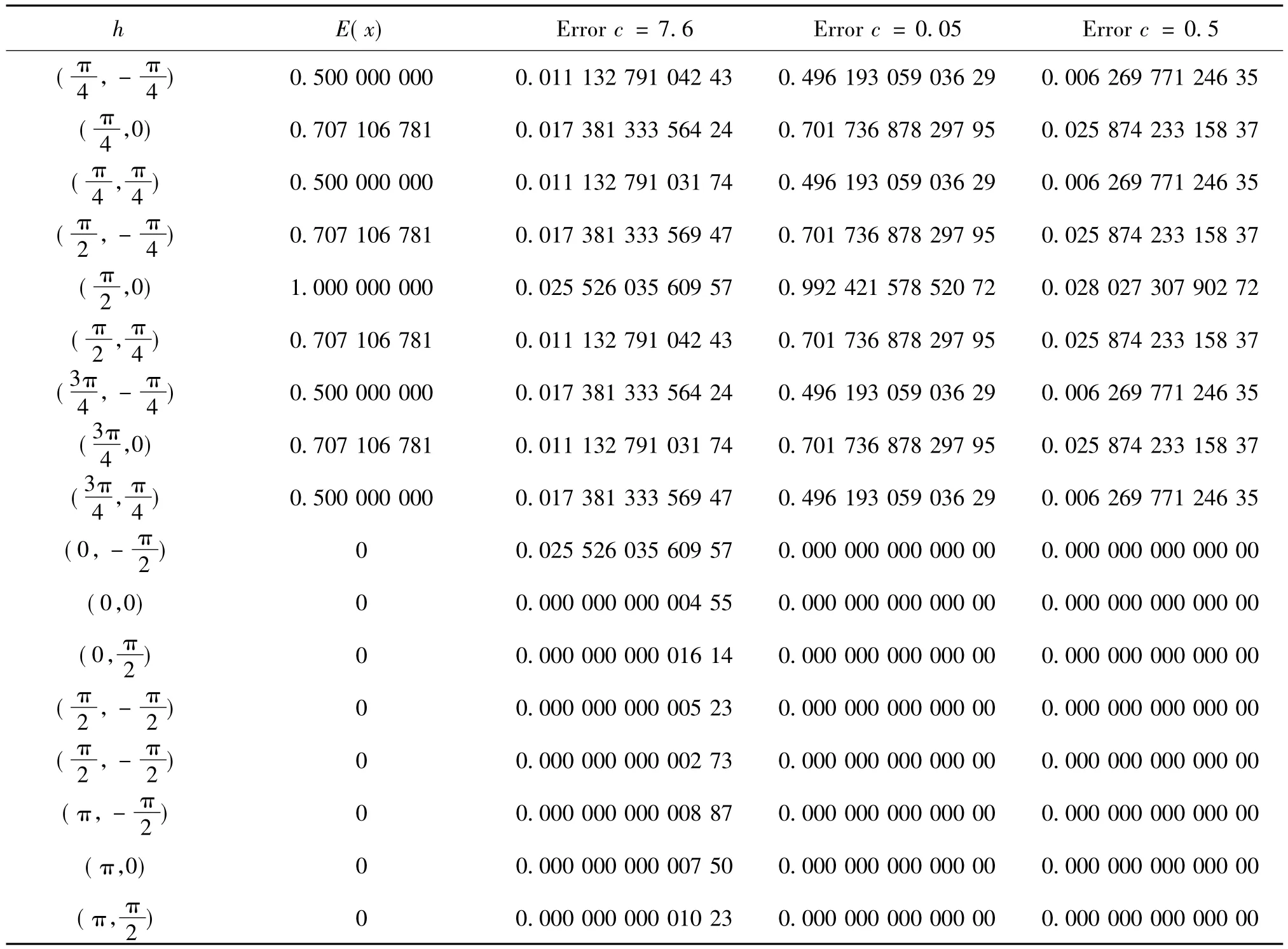
表2 为基函数，不同形状参数时的绝对误差

h E（x）Error c=7．6Error c=0．05Error c=0．5 （π4，－π006 269 771 246 35 （π 4）0．500 000 0000．011 132 791 042 430．496 193 059 036 290．4）0．500 000 0000．011 132 791 031 740．496 193 059 036 290．006 269 771 246 35 （π 4，0）0．707 106 7810．017 381 333 564 240．701 736 878 297 950．025 874 233 158 37 （π4，π 2，－π4）0．707 106 7810．017 381 333 569 470．701 736 878 297 950．025 874 233 158 37 （π2，0）1．000 000 0000．025 526 035 609 570．992 421 578 520 720．028 027 307 902 72 （π 4）0．707 106 7810．011 132 791 042 430．701 736 878 297 950．025 874 233 158 37 （3π2，π 4，－π4）0．500 000 0000．017 381 333 564 240．496 193 059 036 290．006 269 771 246 35 （3π4，0）0．707 106 7810．011 132 791 031 740．701 736 878 297 950．025 874 233 158 37 （3π 4）0．500 000 0000．017 381 333 569 470．496 193 059 036 290．006 269 771 246 35 （0，－π 4，π 2）00．000 000 000 016 140．000 000 000 000 000．000 000 000 000 00 （π 2）00．025 526 035 609 570．000 000 000 000 000．000 000 000 000 00 （0，0）00．000 000 000 004 550．000 000 000 000 000．000 000 000 000 00 （0，π 2）00．000 000 000 005 230．000 000 000 000 000．000 000 000 000 00 （π2，－π 2）00．000 000 000 002 730．000 000 000 000 000．000 000 000 000 00 （π，－π 2，－π 2）00．000 000 000 008 870．000 000 000 000 000．000 000 000 000 00 （π，0）00．000 000 000 007 500．000 000 000 000 000．000 000 000 000 00 （π，π2）00．000 000 000 010 230．000 000 000 000 000．000 000 000 000 00

通过表1和表2注意到，当取相同的形状参数c=0．5，所得到的绝对误差都达到了10－3，但是c=0．05时，表2的绝对误差明显不好．通过数值实验，当径向基函数φ（r）=e－cr2的形状参数c≤0．1时，最大绝对误差为10－3，当形状参数c＞0．1，最大绝对误差精确程度很差;当径向基函数的形状参数1≤c≤4时，最大绝对误差为0．1，当形状参数4≤c≤10，最大绝对误差精确程度可以达到10－3，而在0到1之间取值时，变化比较大．

3 结论

本文成功地用正定径向基函数解一类偏微分方程，通过与精确解作比较，有很小的绝对误差，所以在插值点得到令人满意的数值解，并验证了逼近过程中所得到的矩阵方程有唯一解．

在数值算例部分，选用了不同的径向基函数作为基函数进行数值逼近，当取合适的形状参数时，都可以得到令人满意的数值解．但是注意到，选择相同的步长及不同的形状参数，有不同的绝对误差，所以所得数值解与径向基函数形状参数的选取密切相关．如何选取形状参数，已经引起很多专家学者的注意．一般地，通过2个形状参数，对所得数值解进行比较，逐步选取合适的形状参数，根据经验逐步计算，这种方法并不是很好，甚至有时候不能得到满意的数值解．所以径向基函数的形状参数如何选取，还是需要进一步研究的问题．

另外，本文的数值实验部分，通过数值比较，用Gauss函数φ（r）=e－cr2做为基函数明显优于用φ（r）=作为基函数，那么，一类微分方程哪一类径向基函数可以得到比较好的数值解，这也是需要进一步研究的问题．一般来说，比较常用的是Gauss函数φ（r）=e－cr2作为基函数．

［1］胡建伟，汤怀民．微分方程数值方法［M］．天津:科学出版社，1999．

［2］张池平．数值方法［M］．北京:科学出版社，2006．

［3］MADYCH W R．Miscellaneous error bounds for multiquadric and related interpolators［J］．Comput Math Applic，1992，24 （12）:121-138．

［4］KANSA E J．Multiquadrics:a scarrered data approximation scheme with application to computational fluid dynamics:surface approximations and partial derivative estimates［J］．Comput Math Applic，1990，19（8/9）:127-154．

［5］KANSA E J．Multiquadrics:a scarrered data approximation scheme with application to computational fluid dynamics:parabolic，and elliptic partial differential equations［J］．Comput Math Applic，1990，19（8/9）:146-161．

［6］MADYCH W R，NELSON S A．Miscellaneous error bounds for multiquadic and related inter polators［J］．Comput Math Appl，1992，24（12）:121-138．

［7］MADYCH W R，NELSON S A，NELSON．Multivariate interpolation and conditionally positive definite functions［J］．Math Comput，1990，54（189）:211-230．

［8］KHATTAK A J，LSLAM S U．A comparative study of numerical solutions of a class of KdV equation［J］．Appl Math Comput，2008，199（2）:425-34．

［9］LSLAM S U，HAQ S M，UDDIN．A meshfree interpolation method for the numerical solution of the coupled nonlinear partial differential equations［J］．Eng Anal Bound Elem，2009，33（3）:399-409．

［10］CHEN R，WU Z M．Solving partial differential equation by using multiquadric quasi-interpolation［J］．Appl Math Comput，2007，186（2）:1502-1510．

［11］KHATTAK A J，TIRMIZI S I A，LSAM S U．Application of meshfree collocation method to a class of nonlinear partial differential equations［J］．Eng Anal Bound Elem，2009，33（5）:661-667．

［12］秦伶俐，黄文彬，周喆．径向基函数在无单元方法中的应用［J］．中国农业大学学报，2004，9（6）:80-84．

［13］钱向东．基于紧支径向基函数的配点型无网格方法［J］．河海大学学报，2002，29（1）:96-98．

［14］WU Z M．Compactly supported positive definite radial functions［J］．AICM，1995，4（1）:283-292．

［15］张元林．积分变换［M］．南京:高教出版社，2007．

［16］BEATSON R K，POWELL M J D．Univariate multiquadric approximation:quasi-interpolation to scattered data［J］．Constr Approx，1992，3（8）:275-288．

Application of Radial Basis Functions for Partial Differential Equations

ZHANG Ying-chao*
（School of Mathematics，Guangxi Normal University，Guilin 541004，China）

An algorithm for partial differential equations based on the positive definite radial basis funtions （RBF）approximation scheme is presented．One model problem of the algorithm is given．The comparison is made with the exact solutions of the problem by different shape parameter when different radial basis functions are chosen．Numerical results show that method offers a very high accuracy in computation of the partial differential equation．It shows that choice of shape parameter is important．The obtained coefficient matrix is proved to be nonsingular，that is，matrix equation has a solution．

RBF;numerical solutions;partial differential equation;linear independent

O241．81

A

1000-2537（2011）05-0001-06

2011-02-21

国家自然科学基金资助项目（11171102）

*通讯作者，E-mail:zhych0314@163．com

（编辑沈小玲）