基于方差和峭度的模拟电路故障诊断

吴宏天，刘辉

（湖南师范大学物理与信息科学学院，中国长沙 410081）

基于方差和峭度的模拟电路故障诊断

吴宏天*，刘辉

（湖南师范大学物理与信息科学学院，中国长沙 410081）

针对非线性容差电路故障诊断过程中存在的故障特征提取难的问题，结合小波包分析理论，提出了利用二阶统计量和高阶统计量来描述故障信息的故障特征提取方法，即方差和峭度法，并运用支持向量机作为分类器，形成了一种模拟电路故障诊断的新方法．仿真结果表明，该法能有效的提取故障特征，故障诊断率较高．

小波包变换;方差;峭度;支持向量机

近年来，模拟电路故障诊断的研究已成为现代电路研究领域的热点，并取得了许多成果［1-2］．其故障诊断方法大致可以分为两类:一是测前诊断，如故障字典法;二是测后诊断，如元件参数辨识法等．其中，故障字典法是实用性最强、运用最广的一种方法．但是在现代大规模模拟集成电路中，进行故障检测时需要建立的故障字典过于庞大，加上非线性电路的故障特征难以提取，该法的实现遇到了瓶颈．随着计算机技术以及各种机器学习方法（如支持向量机）的发展和应用，在一定程度上解决了该瓶颈问题．当前，该方法的研究主要集中在两方面:一是如何有效的提取故障电路的特征;二是建立具有高鲁棒性、较强泛化能力的分类器，如各种神经网络等．文献［3］运用峭度和熵作为故障特征，文献［4］提出了基于高阶统计量的方法，文献［5］提出了基于能量的方法，均有较高的诊断率．但是，文献［3］用BP神经网络做分类器时，易收敛于局部极小值，文献［4］存在的不足是只进行高阶分析，遗漏了信号的低阶信息，同理，文献［5］中能量是二阶量，遗漏了信号的高阶信息．针对它们的不足，本文提出了同时运用二阶统计量和高阶统计量来描述故障信息的方法．

1 方差和峭度

在非线性模拟电路故障诊断中，如果把故障电路的电压或电流输出看作信号输出，那么我们就可以用信号处理的方法来提取电路的故障信息和特征．在现代信号处理中，随机信号x的k阶中心矩μk定义［6］为

其中，f（x）为随机信号x的概率密度函数;E（·）表示数学期望;η=E（x）．当k=2时，μ2为x的二阶中心矩，即为信号的方差．方差是常用的二阶统计量，二阶统计量可用来描述信号统计特性的时域特征．对于离散的随机信号，方差表示某一时刻信号偏离期望值的程度，反映了离散的随机信号总体分散情况．在非线性模拟电路故障诊断中，模拟信号经采样后变成离散信号，它的方差必定也不一样．因此，可以用方差来描述故障信息，从而提取故障特征．

由于非线性模拟电路故障诊断的输出信号一般为非高斯、非线性信号，仅用方差来提取故障特征，易造成信息的“遗漏”，而高阶统计量能够很好的解决这个问题，它能够提供有关非高斯、非线性的信息［7］．因此，本文引入峭度这一常用的高阶统计量，作为故障电路的另一个故障特征量，峭度是信号的四阶累积量．设x（t）为平稳随机信号，且有x1=x（t），x2=x（t+τ1），…，xk=x（t+τk－1）（τ为延时量），随机信号x（t）的k阶矩mk定义［8］为

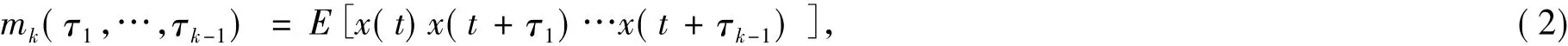
随机信号x（t）的高阶累积量可以用高阶矩来表示，对于零均值信号，四阶累积量［9］为

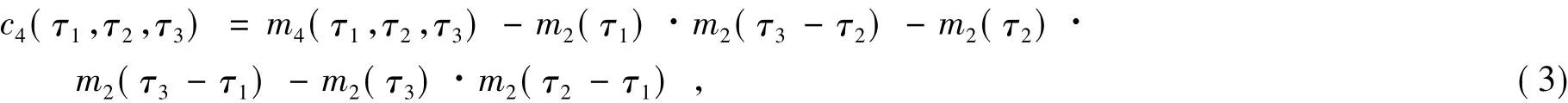
当τ1=τ2=τ3=0时，由式（2）、（3）得:

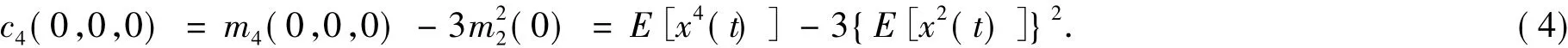
c4（0，0，0）即为信号的峭度，零均值随机信号的归一化峭度定义为［10］

峭度表示随机信号在概率分布中心的尖锐程度，它能够很好的表示信号的瞬时特性．峭度为零的信号为高斯信号，峭度小于零的信号为亚高斯信号，峭度大于零的信号为超高斯信号．在故障诊断中，电路中不同元件发生故障时，输出信号的非高斯性也不同，非高斯信号峭度的绝对值越大，表示故障元件偏离正常值越严重，即元件故障越严重．

综上所述，当非线性模拟电路的不同元件发生故障时，输出信号各频带信号的方差和峭度相应的发生了变化，因此，可以用方差和峭度来提取非线性模拟电路的故障特征，实现故障空间到特征空间的映射．

2 方差和峭度法诊断步骤

本文提出的故障诊断方法主要有以下三个步骤．

2．1 小波包预处理

如果直接计算电路输出信号的方差和峭度，电路元件发生故障时，局部输出信号偏离正常值的变化将会被淹没，即信号的方差变化不明显，也就不能很好的把不同故障类别区分开来．同时，峭度主要描述信号的瞬时特性，即信号高频的特性，不同故障信号的峭度在高频部分的差异最为明显，因而需要知道信号的高频分量．由于小波包分析既能够很好的提取信号的局部信息，又能够把信号高频部分分解为更精细的频带，本文首先对故障信号进行小波包分解和重构，把原信号先分解为各个频带的子信号，然后计算各子信号的方差和峭度．图1为二层小波包分解图［11］．其中，LF表示低通滤波器，HF表示高通滤波器，表示向下抽样．

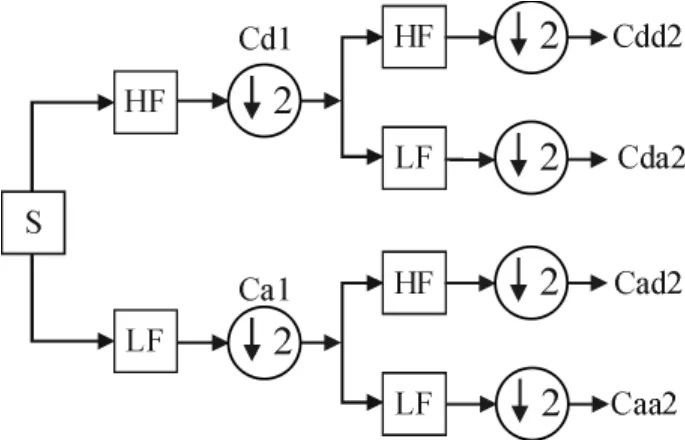
图1 二层小波包分解

2．2 提取特征量

经过小波包分解和重构后，得到各节点的重构信号，零均值化后计算各子信号的方差和峭度（假设进行二层分解），构造特征向量T，归一化后作为训练样本．设S1、S2、S3、S4分别为Caa2、Cad2、Cda2、Cdd2的重构信号，由式（1）、（5）得:

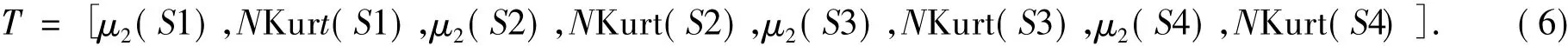
2．3 利用C-SVM进行训练和诊断

支持向量机（Support Vector Machines）是Vapnik等人根据统计学习理论中结构风险最小化原则提出来的一种性能良好的机器学习方法，它能够解决神经网络应用过程中存在的过学习、泛化能力差、收敛于局部最小值和维数灾问题，已被广泛的用来解决多分类、模式识别等问题，是小样本学习的有力工具．本文用LIBSVM软件包进行诊断仿真，并应用其中的C-SVM算法．

3 实验仿真和分析

3．1 电路和故障

为了验证本方法的有效性，采用如图2所示四运放高通滤波器电路进行分析．一般当电路元件值大于等于或小于等于标称值的50%时，则认为电路元件发生了故障（用↑、↓表示）．经灵敏度分析，考虑C1↑、C1↓、C2↑、C2↓、R2↑、R2↓、R3↑、R3↓、R4↑、R4↓共12类故障和正常模式（normal）如表1所示．

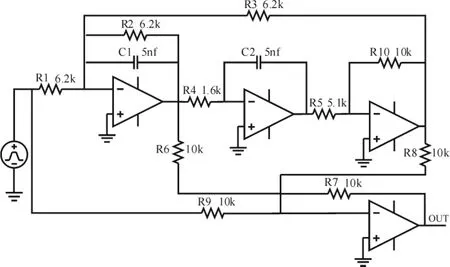
图2 四运放高通滤波器

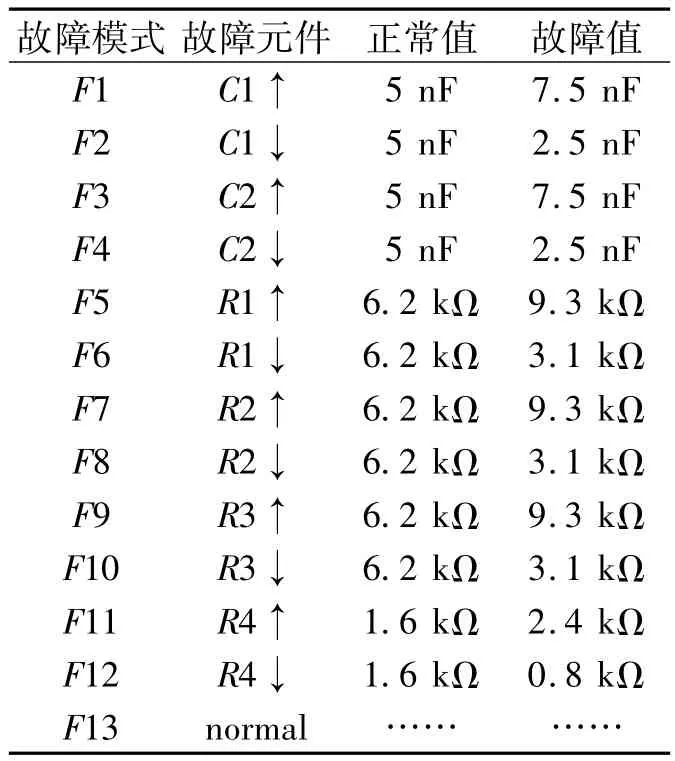
表1

3．2 提取故障特征

用PSPICE软件对电路进行仿真，设电阻和电容分别存在5%和10%的容差且为均匀分布，在输入端施加一个5 V、周期为1 ms，上升沿和下降沿都为10 μs的脉冲源，对电路的每类故障（包括无故障）进行100次Monte Carlo分析．由于在1 ms的周期内电路的响应信号在300 μs后衰减为0，在0～300 μs内，对电路输出（OUT）端的脉冲响应信号采样300个点，得到13个故障类型的采样信号．经过多次实验，运用matlab7．0软件，用双正交db5小波包对采样信号进行二层分解，如图1所示，提取Caa2～Cdd2 4个节点的重构系数（重构信号的信息由重构系数决定），由步骤3．2得到1 300个故障特征样本（650个作为训练样本，650个作为测试样本），如图3所示．

由图3可见，Caa2子信号的方差和峭度能够把F2和F6故障区分开，由Cad2子信号的方差和峭度知，只有F3、F8、F11之间和F1、F7、F12之间不能区分，即对于故障集F3、F8、F11仅有:F3∩F8∩F11≠φ;同样，由Cda2子信号的方差和峭度知，仅有F6∩F9∩F10≠φ、F11∩F12≠φ;由Cdd2子信号的方差和峭度知，只有F7∩F8≠φ、F11∩F12≠φ．显然单一子信号的方差和峭度，不能把所有故障区分开．但是，我们发现综合考虑4个子信号的方差和峭度时，它们并没有共同的非空集，也就是说可以把本例的13类故障进行正确区分．例如，对于Cda2和Cdd2的方差和峭度不能区分的F11和F12故障，运用子信号Cad2的方差和峭度就能够正确区分，其余同理．对于小波包分解的层数问题，如果分层过低，那么易存在共同的非空集合，不能进行正确诊断，分层越多正确诊断的可能就越大，然而过多的层数，会让样本数据过于庞大，占用过多的计算机资源，因此，小波包分解层数以刚好能够把所有故障类别分开为宜．

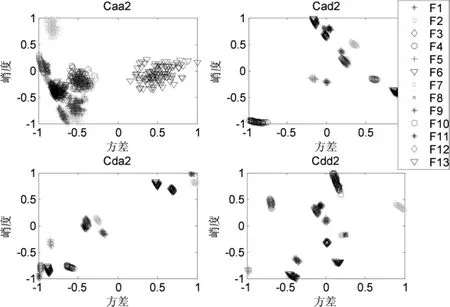
图34 个子信号的归一化方差和峭度

3．3 诊断和比较

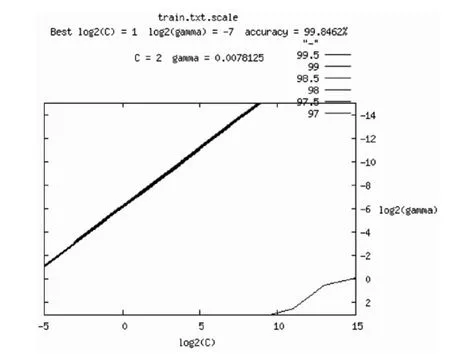
图4 Libsvm参数寻优等高线

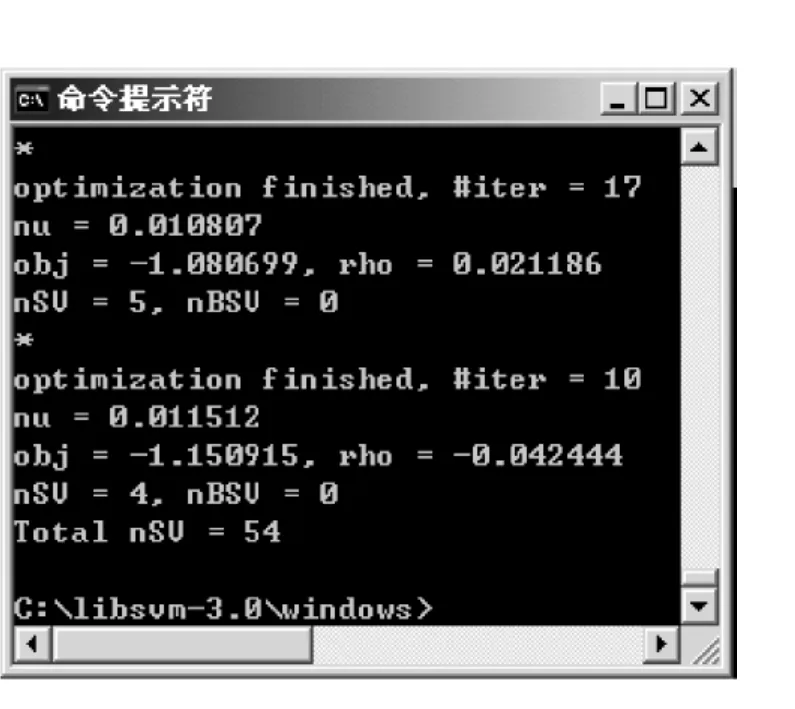
图5 C-SVM训练结果

把650个训练样本输入到libsvm中进行训练，训练和测试代码如下:

训练结果如图5所示．可见，经过训练，由54个支持向量构成了C-SVM多分类器，它能够把训练样本中的13类故障完全分开．用训练好的C-SVM多分类器对测试样本集进行故障诊断，统计结果如表2所示．实验结果表明，只有极少部分样本未能正确分类，可见在非线性模拟电路故障诊断中，方差和峭度能够有效的表征故障信息，利用方差和峭度提取故障特征是一种有效的故障特征提取方法，故障诊断率达到99．69%．

表2 C-SVM诊断结果

文献［12-14］同样以四运放高通滤波器为诊断实例，都以SVM为分类器．文献［13］以输出端（OUT）电压信号的haar小波分解的低频系数作为故障特征，文献［14］以小波变换不同层的高频带能量提取故障特征，文献［15］用提升小波提取电路的低频特征作为故障特征．本文与它们的结果比较列表3，由表3可以看出，利用方差和峭度提取电路的故障特征优于传统的仅以输出信号的小波分解系数和能量作为故障特征的方法，故障诊断率更高．

表3 诊断结果比较

4 结论

本文提出了利用方差和峭度提取模拟电路故障特征的方法，仿真结果表明，该法能够有效的提取电路的故障特征，优于传统的方法．在非线性模拟电路故障诊断中，关键是提取有效的故障特征，小波包分析能够对故障信号提供无损的、精细的频带分解，不同的故障，电路输出端信号各频带所携带的信息也不一样．本方法运用信号的方差和峭度来表征各个故障，只需进行二层小波包分解，加上支持向量机在小样本分类中具有收敛于全局最小值及泛化能力强的优点，是一种有效的故障诊断方法．本法同样适于硬故障诊断．

［1］杨士元．模拟系统的故障与可靠性设计［M］．北京:清华大学出版社，1993．

［2］AMINIAN F．Analog fault diagnosis of actual circuits using neural networks［J］．IEEE Trans．Instr Measu，2002，51（3）: 544-550．

［3］YUAN L F，HE Y G．A new neural-network-based fault diagnosis approach for analog circuits by using kurtosis and entropy as a preprocessor［J］．IEEE Trans．Instr Measu，2010，59（3）:522-528．

［4］SHEN H，TANG J Y．Analog circuit fault diagnosis combing wavelet packet with higher order statistics［C］．2010 2nd International Conference on Signal Processing Systems．Dalian，China，2010．

［5］DIMOPOULOS M G，PAPAKOSTAS D K．Wavelet energy-based testing using supply current measurements［J］．IET Measur Tech，2010（4）:76-85．

［6］张贤达．现代信号处理［M］．北京:清华大学出版社，2002．

［7］何海平，计时鸣．基于高阶统计量的信号分析与处理品［J］．机电工程，2003，20（5）:67-72．

［8］张贤达．时间序列分析—高阶统计量方法［M］．北京:清华大学出版社，1996．

［9］NIKIAS C L，MENDEL J M．Signal processing with higher-order spectra［J］．IEEE Trans．Sign Proces，1993，10:10-37．

［10］张贤达．现代信号处理［M］．北京:清华大学出版社，2002．

［11］飞思科技产品研发中心编著．小波分析理论与matlab7实现［M］．北京:电子工业出版社，2005．

［12］唐静远，师奕兵，张伟．基于支持向量机集成的模拟电路故障诊断［J］．仪器仪表学报，2008，22（6）:1216-1219．

［13］LONG B，HUANG J G．Least squares support vector machine based analog circuit fault diagnosis using wavelet transform as preprocessor［C］．ICCCAS 2008．Beijin，China，2008．

［14］宋国明，王厚军，等．基于提升小波变换和SVM的模拟电路故障诊断［J］．电子测量与仪器学报，2010，24（1）:4-6．

The Analog Circuit Fault Diagnosis Based on Variance and Kurtosis

WU Hong-tian*，LIU Hui

（College of Physics and Information，Hunan Normal University，Changsha 410081，China）

For the problem that it is difficult to extract features when diagnosis the nonlinear and tolerance fault circuits，combined with wavelet packet analysis theory，a fault feature extraction method which used the second-order statistics and the higher-order statistics to describe the fault information was presented，the variance and kurtosis method．By using support vector machine as classifier，it finally formed a new method for the analog circuit fault diagnosis．Simulation results showed that the method can be effective to extract the fault features and has a high accuracy in fault diagnosis．

wavelet packet transform;variance;kurtosis;SVM

O441.5

A

1000-2537（2011）05-0032-05

2011-08-21

湖南省教育厅科研基金资助项目（10C0922）

*通讯作者，E-mail:koutian_wu@163．com

（编辑陈笑梅）