基于小波包和模糊聚类的输电塔结构损伤诊断

谭冬梅，瞿伟廉，秦文科

(武汉理工大学道路桥梁与结构工程湖北省重点实验室，武汉 430070)

输电线塔、电视塔等高耸塔架结构是一类应用广泛的结构型式．其中，塔架结构的主要结构构件以钢管为主，并采用螺栓联结的法兰节点．由于螺栓在长期的风致结构振动中会产生松动，造成螺栓连接节点损伤．如不及时发现，损伤的扩展甚至会引起结构在强风作用下的倒塌，因此及时对法兰联结节点螺栓松动损伤的诊断是十分必要的．在结构损伤识别的实践中，由于实际损伤样本很难获得，而且用于损伤诊断的分类器得不到足够的知识学习，导致识别误差较大．模糊聚类分析由于设计简单，解决问题范围广，现已在许多领域得到广泛应用．

结构发生损伤后，会引起固有频率、振型、阻尼等模态参数发生变化，经过测试得到的振动信号包含有非平稳成分，这些非平稳成分反映出丰富的损伤信息．而传统的基于傅里叶变换的时频信号分析方法仅能提供信号的平均统计结果，难以准确描述局部微弱的特征．小波变换是一种全新的时频分析方法，对非平稳信号具有宽频响应的特点．在低频处有较高的频率分辨率，在高频处有较高的时间分辨率，具有优良“变焦” 性能的时频局部化特性，可以聚焦到信号的任意细节，适合分析非平稳信号[1]．而小波包(wavelet packet，WP)分析是多分辨分析基础构造的一种更精细的分析方法，它将频带进行多层次划分，对多分辨分析没有细分的高频部分进一步分解，能够把任何信号(平稳的或非平稳的)映射到一个小波伸缩而成的一组基函数上，在通频范围内得到分布在不同频段内的分解序列，具有对非平稳信号进行局部化分析的功能．因此当结构发生不同程度的损伤时，小波包分解频带能量分布不同，所以可以用小波包分量能量的变化反映结构的损伤信息．Han 等[2]将结构的动力测试信号利用小波包分解得到的小波包能量比率指数去识别损伤．Sun 等[3]利用小波包变换将信号进行分解得到小波包分量能量，然后用神经网络进行损伤诊断．Reda 等[4]提出了将模糊模式识别的损伤识别方法用于结构的健康监测，其中在智能结构健康监测中，通过增加模糊子集的数量来提高模式识别．

本文提出了以小波包分量能量为损伤特征向量，利用模糊聚类分析方法对输电线塔节点联结螺栓松动进行损伤识别．通过对一个简化的3 层输电线塔结构模型进行激振，得到结构法兰联结节点螺栓松动的损伤应变信号，然后再由小波包变换对测得的振动信号进行小波包分解，提取小波包分量能量作为损伤特征向量，以此作为模糊聚类的样本集．然后确定聚类类别数，由模糊聚类分析实现输电线塔结构的损伤诊断．试验结果表明，该方法能够有效地识别输电线塔结构的损伤．

1 小波包基本理论

1.1 小波分析

为了克服窗口傅里叶变换单一的缺陷，数学研究者提出了一种时-频分析方法，即小波分析[5]．

设ϕ(t)为一平方可积函数，也即ϕ(t)∈L2(R)，若其傅里叶变换ψ(ω)满足条件

则称ϕ (t)为一个基本小波或小波母函数，式(1)为小波函数的可容许性条件．

将任意L2(R)空间中的函数(f)t在小波基下进行展开，称这种展开为函数(f)t的连续小波变换(continuous wavelet transform，CWT)，其表达式为

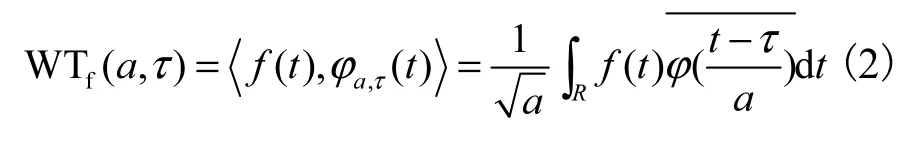
式中：WTf(a,τ)为小波变换系数；ϕa,τ(t)为依赖于参数a和τ的小波基函数；a为尺度因子；τ为平移因子．对尺度及平移因子进行离散化即得到离散小波变换．

1.2 小波包分析

由小波变换(wavelet transform，WT)得到的小波包技术[5-6]能够把任何信号映射到一个小波伸缩而成的一组基函数上，在通频范围内得到分布在不同频段内的分解序列，它具有对信号特征的自适应性，因而能够有效地显示信号的时-频特征．

假定共轭滤波器h(n)满足

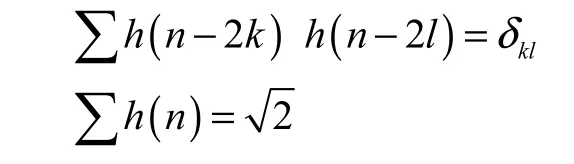
令g(k)=(−1)kh(1−k)，按双尺度关系，定义一列递归函数

式中：μ0(x)可以定义为尺度函数ϕ(x)；μ1(x)为小波基函数ψ(x)．称由标准正交化的多尺度生成元ϕ(x)导出的函数为关于ψ(x)的小波包．小波包的完整性和正交性使原始信号的信息得到完整保留．

经过小波包分解后，信号被分解到各个频段，尤其是对高频段的信息进行分解．再对小波包分解系数进行重构，提取各频带范围的信号．

假定对一时域信号进行3层小波包分解，并对小波包分解系数进行重构，只对第3层的所有节点进行分析，则总信号可以表示为

式中：S表示总信号；30S，31,S…，S37表示小波包分解的低频或高频系数的重构信号．

由于输入信号是一个随机信号，其输出也是一个随机信号．设S 3 j(j= 0,1,…,7)对应的能量为E3 j(j= 0,1,…,7)，则有

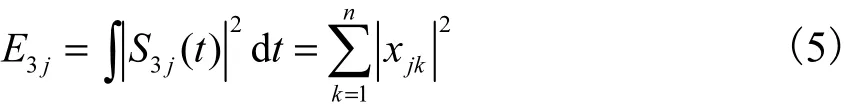
式中xjk(j=0,1,…,7;k=1,2,…,n)表示重构信号S3 j(j = 0,1,…,7)离散点的幅值．由于结构出现损伤时，会对各频带内信号的能量有较大影响，因此可以能量为元素构造一个特征向量，即

2 模糊C均值聚类算法

聚类分析方法大致可以分为4 种类型：谱系聚类法、基于等价关系的聚类法、图论聚类法和基于目标函数的聚类方法．前3 种方法由于各种原因实际应用不够广泛，普遍受欢迎的是第4 种方法，即基于目标函数的聚类方法，在该方法中，C 均值聚类算法应用最为广泛．它包括硬C 均值(hard C-mean，HCM)聚类算法和模糊C 均值(fuzzy C-mean，FCM)[7]聚类算法，它们均是把聚类分析归结成一个带约束的非线性规划问题，依据最小二乘原理采用迭代法优化目标函数来获得对数据的最优模糊划分和聚类．其中FCM 算法设计简单，解决问题范围广[8]．

给定数据集X={x1,x2,…,xn}⊂R 为模式空间中n个模式的一组有限观测的样本集，对给定样本集的X聚类分析就是要产生 X 的聚类类别数c(2 ≤c≤n)划分．硬聚类算法将每个辨识对象严格地划分为属于某一类．不过在实际中一些对象并不具有严格的属性，它们可能位于两类之间，这时采用模糊聚类可以获得更好的效果．FCM 算法是由隶属度确定每个数据点属于某个聚类程度的一种聚类算法[9]，准备将给定数据集X分为c类，设X中的任意样本xk对第i类的隶属度为uik(0 ≤uik≤1)；该分类结果可以用一个c×n阶矩阵U来表示，该矩阵称为模糊划分矩阵．

FCM 的一般描述为

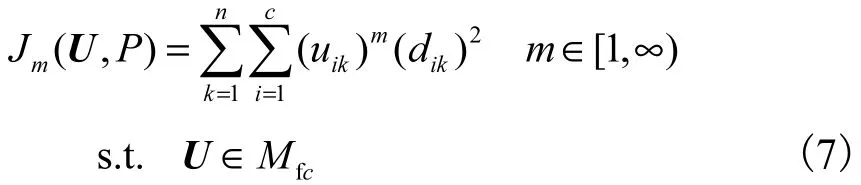
式中：m称为加权指数，又称作平滑参数；fcM为X的模糊c划分空间，

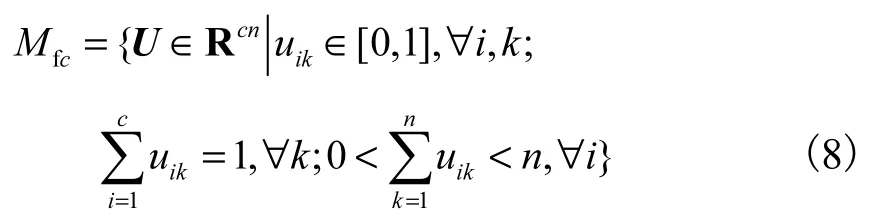
上述目标函数中，样本x k与第i类聚类原型pi之间距离度量的一般表达式定义为

式中：A为s×s阶的对称正定矩阵，当A取单位矩阵I时，式(9)对应于欧氏距离．

聚类的准则是求取Jm(U,P)的极小值min{Jm(U,P)}[10]．

由于矩阵U中各列都是独立的，因此

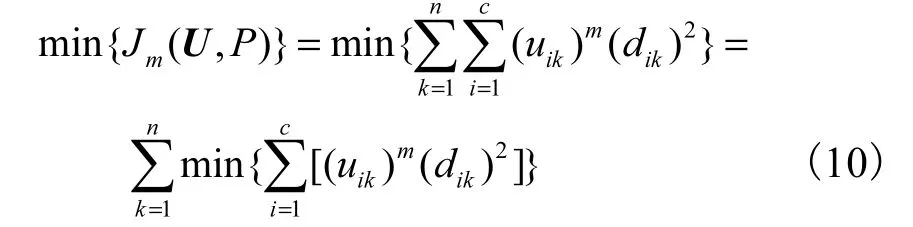
考虑到d ik可能为0，应分2 种情况加以讨论．对于 ∀k，定义集合I k和为

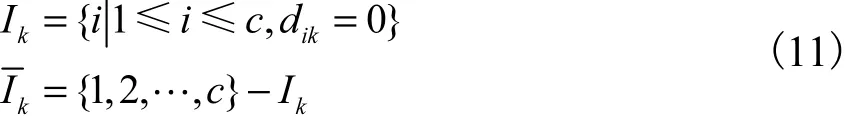
使得Jm(U,P)为最小的u ik值为

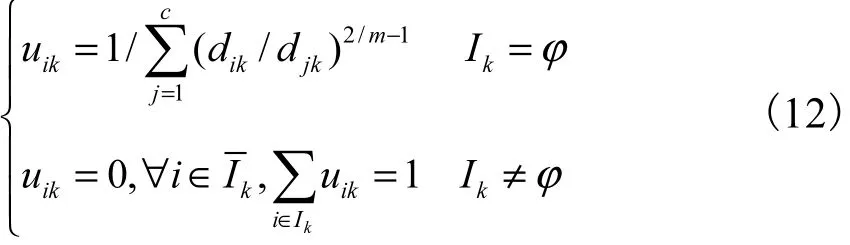
用类似方法可获得Jm(U,P)为最小值时pi的值，

若数据集X、聚类类别数c和加权指数m值已知，就能确定最佳模糊分类矩阵和聚类中心．

3 试 验

为了验证基于小波包变换和模糊聚类的输电线塔结构损伤诊断的适用性，采用一个简化3 层的输电线塔结构做试验研究．输电线塔的简化模型和法兰数目及其位置见图1，其中图1(a)中黑色有标号位置为法兰位置，模型共有12 个法兰．图1(b)是试验室平台上的缩尺模型．法兰模型如图2(a)所示，每个法兰上有6 个螺栓，图2(b)中F 是模型试验中施加一定频率的简谐激励的位置，在每个法兰连接处的螺栓外沿处张贴应变片的位置如图2(c)所示．

当在图2(b)中激励加载位置F 点分别对输电线塔结构施加激励频率为20,Hz 和6,Hz 的简谐激励时，对图1(a)中模型标注位置为3-1 和3-8 等法兰连接处的应变变化情况进行了测试研究，研究结果发现当激励频率越接近低频或者结构的自振频率时，结构的反应越敏感，而且与激励成大致相同的谐波曲线．因此在进行输电线塔损伤识别的试验过程中，选择激励频率为6,Hz 的简谐激励来对结构进行简谐激振．

从图2(a)中的法兰模型可以看出，每个法兰有6个螺栓连接．为了模拟破坏，对图1(a)中的3-8 处的法兰选择3 种损伤工况：①结构完好，法兰盘中的所有螺栓无松动；②法兰盘中只有1 个螺栓松动，其他螺栓无松动；③法兰盘中不仅有1 个螺栓松动，其相邻的2 个螺栓也微微松动．由图2(c)中可以看到，在法兰盘螺栓松动外边沿张贴应变片．试验过程中，对结构施加激励频率为6,Hz 的简谐激励，并对每种损伤工况分别采集8 组应变数据，将得到的24 组各工况应变信号利用Daubechies 小波族的db1 小波进行3 层小波包分解，共分为8 个频段，并对小波包分解系数进行重构，提取各频带小波包分量能量．其中分别对工况1、工况2 和工况3 的第8 组信号进行小波包分解，并对小波包分解系数进行重构后的小波包节点如图3 所示．图3(a)为工况1 的重构的小波包节点，图3(b)为工况2 的重构的小波包节点，图3(c)为工况3 的重构的小波包节点．对各工况提取的各频带的小波包分量能量见图4．

图1 输电塔结构模型Fig.1 Transmission tower structure model

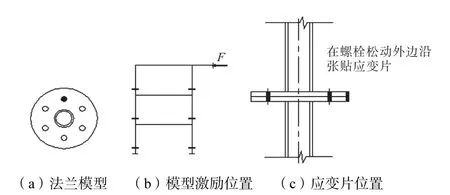
图2 法兰模型、激励加载和应变片贴放位置Fig.2 Flange model，excitation load and strain gauge Fig.2 placement

图3 工况1、工况2和工况3的重构小波包节点Fig.3 Reconstructed nodes of wavelet packet of case 1，case2 and case 3

从图4 中可以看出，在3 种损伤工况中，只有一个螺栓松动的工况2 的小波包分量能量最低．在频带1～3 之间，工况3 的小波包分量能量高于工况1，而在频带4～8 之间，工况3 的小波包分量能量又低于工况1．由此得出，随着法兰盘螺栓松动数量的增加，小波包分量能量并没有随着损伤加重呈大致增加或降低的趋势．

图4 3种工况的小波包分量能量在0～8频带的分布Fig.4 Distribution of wavelet packet component energy of three cases in the 0—8 frequency band

将测试得到的24 组小波包分量能量作为模糊聚类的样本集，见表1．

从表1 中可以看出，对于编号为1～16 的数据样本，约65%以上的小波包分量能量集中在频带1～4之间，大约35%以上的小波包分量能量集中在频带1～2 之间；对于编号为17～24 的数据样本，约90%以上的小波包分量能量集中在频带1～4 之间，大约80%的小波包分量能量集中在频带1～2 之间．从以上分析可以得到，无论工况1、工况2 和工况3，每组数据的小波包分量能量大部分都集中在低频带内，即低频段所含损伤信息较丰富，尤其对于损伤最为严重的工况3，这些特征更为明显．

对上述24 组数据进行标准化处理，使原始数据都压缩在[0，1]闭区间内．然后选择聚类类别数为3，利用模糊C 均值聚类算法对其进行模糊划分，则24组数据经模糊聚类后的结果见表2．其中分类号1 对应的是工况1，分类号2 对应的是工况2，分类号3对应的是工况3．

表1 模糊聚类数据样本Tab.1 Samples of fuzzy clustering data

表2 数据经模糊聚类后的结果Tab.2 Identification results based on fuzzy clustering

从表2 中可以看出，在试验过程中，由于试验条件、人工操作和监测设备本身会随着环境温度、湿度、电源电压不稳定、振动等因素的影响而产生微小变化，因而在试验数据中会产生偶然误差，因此本是工况1 的样本3 经过模糊聚类后被归类到工况2，但其余各损伤工况都得到了很好的识别．因此原始数据经过模糊聚类后，可以对各损伤工况进行很好的划分，从而可以将该方法有效地用于输电线塔结构的损伤诊断．

4 结 语

本文提出了基于小波包变换与模糊聚类实现对输电线塔结构的损伤识别方法．首先对结构的振动测试信号进行小波包分解，提取小波包分量能量作为损伤特征向量，以此作为模糊聚类的样本集，然后确定聚类类别数，利用模糊聚类分析对输电线塔结构进行损伤诊断．为了验证该方法，对一个简化3 层输电线塔结构模型进行了试验研究，研究结果表明，该方法能够有效地对输电线塔结构进行损伤识别．

［1］何正嘉，訾艳阳，孟庆丰，等. 机械设备非平稳信号的故障诊断原理及应用[M]. 北京：高等教育出版社，2001.He Zhengjia，Zi Yanyang，Meng Qingfeng，et al.Default Diagnosis and Application of Non-Stationary Signal in Mechanical Equipment[M]. Beijing：Higher Education Press，2001(in Chinese).

［2］Han Jiangang，Ren Weixing，Sun Zengshou. Wavelet packet based damage identification of beam structures[J].InternationalJournalofSolidsand Structures，2005，42(26)：6610-6627.

［3］Sun Z，Chang C C. Statistical wavelet based method for structural health monitoring[J].ASCE Journal of Structural Engineering，2004，130(7)：1055-1062.

［4］Reda T M M，Lucero J. Damage identifica-tion for structural health monitoring using fuzzy pattern recognition[J].Engineering Structure，2005，27 (12)：1774-1783.

［5］彭玉华. 小波变换与工程应用[M]. 北京：科学出版社，2003.Peng Yuhua.The Wavelet Transform and Engineering Application[M]. Beijing：Science Press，2003(in Chinese).

［6］Ortiz E，Syrmos V. Support vector machines and wavelet packet analysis for fault detection and identification[C]//International Joint Conference on Neural Networks. Vancouver B C，Canada，2006：3449-3456.

［7］Donovan G C，Geronimo J S，Hardin D P，et al. Construction of orthogonal wavelets using fractal interpolation functions[J].SIAM Journal on Math Analysis，1996，27(4)：1158-1192.

［8］张 磊，董 慧，杨润玲. 基于模糊聚类遗传算法的图像分割方法研究[J]. 现代电子技术，2009，32(16)：120-122.Zhang Lei，Dong Hui，Yang Runling. Research on the method of fuzzy clustering image segmentation based on genetic algorithm[J].Modern Electronics Technique，2009，32(16)：120-122(in Chinese).

［9］匡 泰，朱清新，孙 跃. FCM 算法用于灰度图像分割的初始化方法的研究[J ]. 计算机应用，2006，26(4)：2784-2786.Kuang Tai，Zhu Qingxin，Sun Yue. Research on initialization of image segmentation with FCM algorithm[J].Journal of Computer Applications，2006，26(4)：2784-2786(in Chinese).