缺失数据下广义线性回归拟似然估计的相合性和渐近正态性

赵晶晶，张晓冉，徐玉民

(燕山大学 理学院 河北 秦皇岛 066004)

缺失数据下广义线性回归拟似然估计的相合性和渐近正态性

赵晶晶，张晓冉，徐玉民

(燕山大学 理学院 河北 秦皇岛 066004)

研究了形如L(β)=ΣiZi(yi-μ(ZiTβ))=0的拟似然方程在协变量数据有缺失时，方程未知参数估计的相合性和渐近正态性.假设存在协变量数据完整的一个有效样本，且是总样本的一个简单随机子样本，基于EM算法，提出了一种新的处理协变量中有不完整数据的拟似然方程的求解法，即通过有效数据线性预测补足协变量数据缺失部分，并且证明了当样本量n→∞，在满足一些正则条件下所得出的新拟似然方程有解，且该解具有相合性和渐近正态性.

广义线性模型； 拟似然估计； 不完全协变量； 相合性； 渐近正态性

0 引言

在广义线性模型中，设响应变量yi(i=1,…,n)相互独立，服从指数型分布

exp(θiTyi-b(θi))dv(yi),i=1,…,n,

(1)

其中协变量Zi为q维列向量，yi的期望和线性预测因子ZiTβ有关系ui=h(ZiTβ)，其中h:Rq→Rq是一对一光滑映射，β∈Rq是未知的回归参数，β*为其真值.函数h的逆称为联系函数，μi=E(yi)=b′(θi)，di=Var(yi)=b″(θi).不难得到似然方程

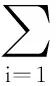
(2)

拟似然方法的提出舍弃了响应变量服从指数型分布的假定，并分离了均值和方差的结构.事实上只需正确指定其一阶距和二阶距就可在适当条件下得到参数的相合估计及其大样本性质[1].文献[2]提出只要均值函数假定正确，就可以预先假定响应变量的“工作分布”进而用“工作方差”Λ(·)替代(2)中的真实方差∑(·)，并保留响应变量独立的假设，从而得到拟似然方程

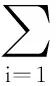
文献[3-7]研究了形如

L(β)=ΣiZi(yi-μ(ZiTβ))=0

(3)

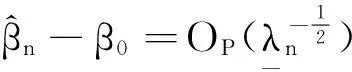
本文研究形如(3)的拟似然方程在协变量数据部分缺失时参数估计的相合性和渐近正态性.当协变量数据有缺失时，方程(3)无法求解.由于有效样本是总样本的一个简单随机子样本，可以只根据有效样本估计出β.然而，舍弃不完全的观测会导致估计效能的减小，尤其当有效数据占据比例较小时.文献[8]对GLM中不完整的协变量数据问题，基于投影思想通过线性补足缺失协变量数据，在一定正则条件下得到了似然方程(2)参数估计的相合性和渐近正态性.受其思想启发，类似于EM算法[9]，本文提出通过补足协变量缺失数据来得出(3)相合性和渐近正态性的方法.

假定能够完全观测到的Zi是来自容量为n的总样本的一个随机子样本，子样本大小为m，称这个子样本为有效样本，剩余的n-m个为无效样本,且有效比m/n→ρ∈(0,1]当n→∞.记V={1,…,m}和NV={m+1,…,n}分别为有效样本和无效样本的标识.记Zi=(ZiT,XiT)T，其中Zi表示在样本中总能观测到的协变量向量部分，Xi表示只能在有效样本中观测到的协变量向量部分.当协变量能够完全观测到时仍记为Zi.对于一般的有自然联系的GLM，

(4)

是基于有效数据的拟似然估计方程.如果有效样本是有代表性的，则可用作无偏估计方程.

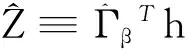
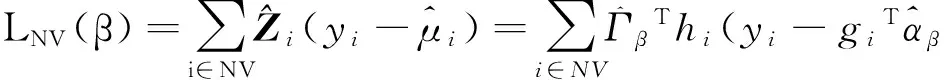
(5)

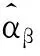
1 相合性和渐近正态性

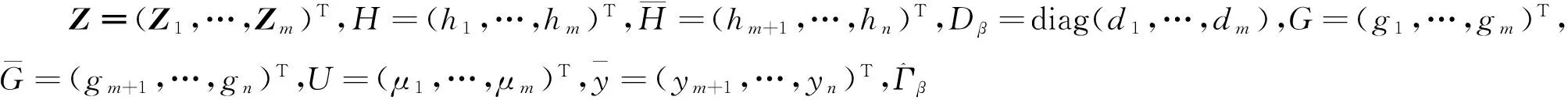
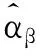
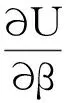
其中,

对于β*邻域B内的β，在一些正则条件下有

上式是由于E(hgT){E(ggT)}-1=(0,Ir)，Ir是维数为r=dim(h)单位矩阵，0表示r维0向量.由于

F(β)≡-limnn-1∂L(β)/∂β=ρE(dZZT)+(1-ρ)E(dZhT)[E(dhhT)]-1E(dhZT).

定理1在满足以下正则条件下

1)β∈Θ，Θ是Rq的一个紧的凸的子集，真实的参数β*位于Θ的内部；

2)(yi,Zi,Xi)，i=1,…,n，独立同分布；

3)对每个Zi，μ关于β二次可导；

4)矩阵F*≡F(β*)存在且正定；

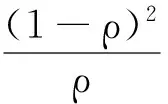
其中

2 定理的证明

2.1相合性

当满足下列条件时β的估计是相合的：

(a)∂L(β)/∂β的分量在Θ中存在且是连续的;(b)当n→∞矩阵n-1∂L(β)/∂β在β*处以概率1负定；(c)n-1∂L(β)/∂β依概率一致的收敛到F(β)，对于β∈B；(d)当n→∞，n-1L(β*)=OP(1).

根据定理1条件3)可知(a)成立；根据条件4)和定理1上面的结果可知(b)成立；根据5)，并对在巴拿赫空间取值的随机变量运用强大数定律可获得n-1∂L(β)/∂β的一致收敛性[10]，因此(c)成立；最后根据第一节后面部分的讨论可知(d)成立.

2.2正态性

=Γ*TE{h(y-gTα*)2hT}Γ*.

因此由中心极限定理可知A服从均值为零方差为ΣNV的渐近正态分布.由条件2)知

记R=E(ggT)，

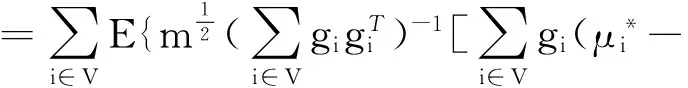
=R-1E{g(μ*-gTα*)}{g(μ*-gTα*)}TR-1

=R-1E{g(μ*-gTα*)2gT}R-1=Λα.

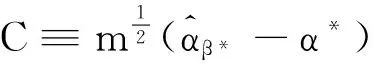
Σα=Var(Γ*TB·C)

=Γ*TBVar(C)BTΓ*=Γ*TE(hgT)ΛαE(ghT)Γ*

=Γ*TE(hgT){E(ggT)}-1E{g(μ*-gTα*)2gT}{E(ggT)}-1E(ghT)Γ*

=Γ*TE{h(μ*-gTα*)2hT}Γ*.

上式是因为E(hgT){E(ggT)}-1=(0,Ir)，g=g(y,Z)≡(y,hT)T.

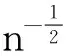
=(1-ρ)E[Z(y-μ*)(gTα*-

μ*)gT]{E(ggT)}-1E(ghT)Γ*.

记ΣC=E[Z(y-μ*)(gTα*-μ*)gT]{E(ggT)}-1E(ghT)Γ*，又因为E(hgT){E(ggT)}-1=(0,Ir)，g=g(y,Z)≡(y,hT)T，因此

ΣC=E[Z(y-μ*)(gTα*-μ*)gT]{E(ggT)}-1E(ghT)Γ*

=E[Z(y-μ*)(gTα*-μ*)hT]Γ*.

由于gTα*是μ*基于g=g(y,Z)≡(y,hT)T的最小二乘估计，可以写成gTα*=αy*y+(1-αy*)hTθ*，其中hTθ*为μ*基于h的最小二乘估计，

αy*是α*对应于y的分量，则代入上式化简可得

=E{αy*Z(y-μ*)2hT}Γ*=αy*E(d*ZhT)Γ*.

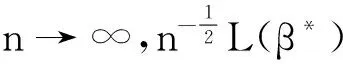
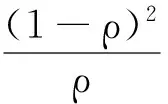
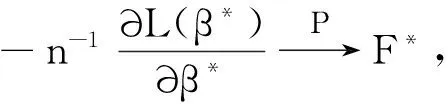
[1] Alan A. Categorical Data Analysis[M].2nd Edition.New York:Wiley,2002：115-153.

[2] Liang K Y, Zeger S L. Longitudinal data analysis using generalized linear models[J].Biometrika,1986,73(1):13-22.

[3] 张三国, 廖源. 关于广义线性模型拟似然估计如相合性的几个问题[J]. 中国科学A辑,2007,37(11)：1368-1376.

[4] Chen K. Strong consistency of maximum quasi-likelihood estimators in generalized linear models with fixed and adaptive designs[J].Ann Statist,1999,27(4)：1155-1163.

[5] 高启兵, 吴耀华. 广义线性回归拟似然估计的强相合性[J]. 数学年刊A辑, 2004，25(6)：705-710.

[6] 高启兵,吴耀华.广义线性回归拟似然估计的渐近正态性[J]. 系统科学与数学,2005,25(6)：738-745.

[7] 阎莉,陈夏.缺失数据下广义线性回归拟似然估计的强相合性[J]. 陕西师范大学学报：自然科学版，2010,38(2):15-17.

[8] Chen Y H,Chen H. Incomplete covariates data in generalized linear models[J].Journal of Planning and Inference,1999,79(2):247-258.

[9] 茆诗松,王静龙,濮晓龙.高等数理统计[M].北京:高等教育出版社，2007：427-435.

[10] Fahrmeir F,Kaufmann H. Consistency and asymptotic normality of the maximum likelihood estimatorin generalized linear models[J]. Ann Statist,1985,13(1):342-368.

ConsistencyandAsymptoticNormalityofQuasi-likelihoodEstimatorinGeneralizedLinearModelswithMissingData

ZHAO Jing-jing，ZHANG Xiao-ran，XU Yu-min

(SchoolofScience，YanshanUniversity，Qinhuangdao066004，China)

The consistency and asymptotic normality of quasi-likelihood estimating equation asL(β)=ΣiZi(yi-μ(ZiTβ))=0 was considered when part of the covariates were incomplete in generalized linear models. It was assumed that there existed a validation sample in which the data was complete .And it was a simple random subsample from the whole sample. Based on the EM-solution, a new method was proposed to estimate the regression coefficients with incomplete covariables by linear predict the incomplete co-variable data.When it was sufficiently large, the estimate was consistency and asymptotic normality under some regularity conditions.

generalized linear models; quasi-likelihood estimation; incomplete covariable; consistency; asymptotic normality

O 212.4

A

1671-6841(2011)03-0043-05

2010-05-28

赵晶晶(1986-)，女，硕士研究生，主要从事广义线性模型参数估计性质研究，E-mail:zhaojj0418@126.com.