图的测地全控制数

赵 敏

(中国计量学院理学院,浙江杭州310018)

近三十多年来,图的控制数理论已成为图论的一个重要研究领域,在相关学科领域,例如计算机科学、通讯网络、编码理论、运筹学以及社会学等领域具有广泛的应用.根据不同的应用背景,人们定义了多种控制参数[1-5].关于图的控制理论的全面研究进展可参看文献[6-7].1993年,Harary等在文献[8]中定义了图的测地集的概念并进行了研究;Escuadro与Hansberg等在文献[9]与[10]中,将测地集与控制集的概念结合提出了测地控制集的概念.本文将测地集与全控制集的概念结合引入测地全控制集的概念,给出路与圈上的测地全控制数的确定值,并证明弦图上的测地全控制集问题是NP-完全的.

1 基本概念与符号

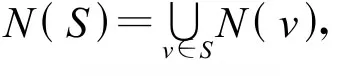
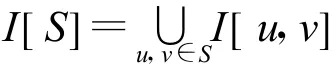
设S⊆V(G),若 N[S]=V(G),则称 S为图G的控制集;若 N(S)=V(G),则称S为图G的全控制集.最小控制集(全控制集)的基数称为控制数(全控制数),记为γ(G)(γt(G)).基数恰为 γ(G)(γt(G))的控制集(全控制集)称为G的γ-集(γt-集).若S为G的控制集(全控制集),则称S控制(全控制)图G.

若S⊆V(G)既是测地集,又是控制集,则称S为测地控制集,最小测地控制集的基数称为测地控制数,记为 γg(G).若S既是测地集,又是全控制集,我们称S为测地全控制集,最小的测地全控制集的基数称为测地全控制数,记为γgt(G).文中其它未加定义的术语和记号可参看文献[1]和[2].

2 基本结论

根据定义,立即可得到下列结论:

定理2.1 如果图G是阶数为n≥2的连通图,则下列不等式成立:

定理2.2 设图G为最小度δ≥2的任意图.如果图G的围长至少为6,则下式成立:

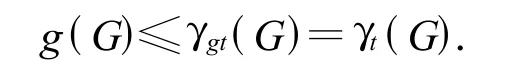
证明 设D是图G的一个最小全控制集,并记X=V(G)[D].假设 x∈X,则 x在D 中有一个邻点u.由于δ≥2,存在一个点 v∈N(x){u}.因为图G的围长至少为6,即G为无三角形图,所以uv∉E(G).假设 v∈D,则 x∈I[{u.,v}]⊆I[D],矛盾.因此v∈VD且存在一点z∈D∩N(v).由于图G的围长至少为6,我们有d(u,z)≥3,那么有 x,v∈I[{u,z}]⊆I[D],矛盾.因此,X是空集且D是G的一个测地全控制集,这表明γgt(G)≤|D|=γt(G).根据定理2.1,结论成立.

下面证明一个关于路的测地全控制数的有用结论.

引理2.3 设Pn是阶数为n≥8,点集为V(Pn)={v1,v2,…,vn}的路.若 Pn-6为点集为 V(Pn-6)={v4,v5,…,vn-3}的路,则 γgt(Pn)=γt(Pn-6)+4.

证明 设D为Pn的一个γgt-集.令X={v1,v2,vn-1,vn},由于Pn的每个测地集均包含点v1,vn,且D也是Pn的全控制集,所以有X⊆D.又由于X仅全控制集合X1={v1,v2,v3,vn-2,vn-1,vn},因此DX为Pn-6的最小全控制集.这表明 γgt(Pn)-|X|=|D|-4=|DX|=γt(Pn-6),即 γgt(Pn)=γt(Pn-6)+4.

Zwierzchowski[11]给出了路和圈的全控制数的确定值:

定理2.4[11]设Pn和Cn分别是阶数为n≥2与n≥3的路和圈.那么

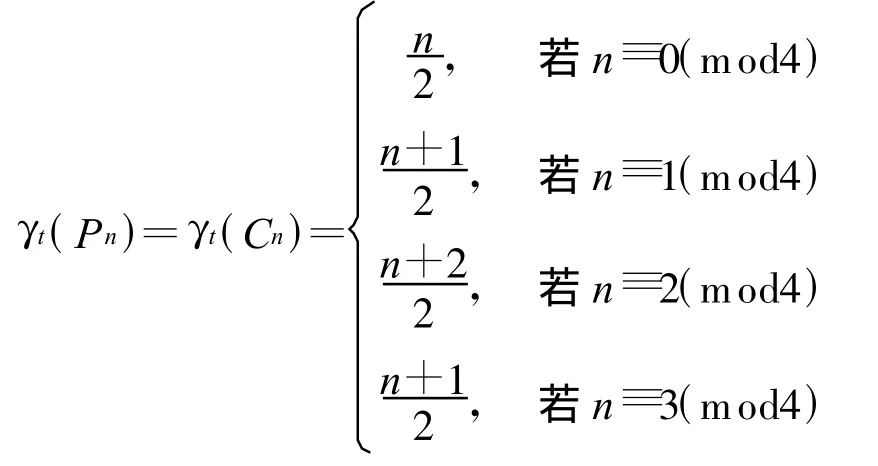
下面我们给出路和圈上测地全控制数的值.

定理2.5 设Pn和Cn分别是阶数为n≥2与n≥6的路和圈.那么

且

定理得证.

3 复杂性结论

如果图G不含长度至少为4的导出圈,则称图G为弦图.在文献[12]中,作者证明了确定给定弦图是否存在一个基数不大于k的测地集问题是NP-完全的.我们将证明对于测地全控制集有相同结论成立.我们定义下列判定问题:

测地全控制集

实例:一个图G与一个整数k.

问题:图G是否存在一个基数至多为k的测地全控制集？

全控制集

实例:一个图G与一个整数k.

问题:图G是否存在一个基数至多为k的全控制集？

众所周知,全控制集是NP-完全的,甚至限制在弦图上也是如此[13].下面我们将证明可在线性时间内将弦图上的全控制集问题转换为弦图上的测地全控制集问题.

定理3.1 求解弦图的测地全控制集问题是NP-完全的.

证明 因为测地集问题与全控制集问题都属于NP类问题,且测地集与全控制集的并为测地全控制集,所以测地全控制集问题也属于NP类问题.

设(G,k)是全控制集问题的一个实例,且G是弦图.设图G'是由图G按下列方式得到的:对于每个点u∈V(G),增加三个新的点xu,yu,zu和三条边uxu,xuyu,yuzu.注意到图G'仍然为弦图,且令k′=k+2n(G).

设图G有一个全控制集D满足|D|≤k.令D′=D ∪{yu,zu|u∈V(G)},则D′是图G′的一个测地全控制集,且|D′|≤k+2n(G)=k′.

相反地,设图G′有一个测地全控制集D′且|D′|≤k′,则显然对任意 u∈ V(G)有 yu,zu∈D′.不失一般性,可假设 xu∉D′.否则,若 xu∈D′,对任意点v∈NG(u),我们可断定不可能有u∉D′且v∈D′.若不然,若 u∉D′且v ∈D′,则 D″=D′{xu}也是图G′的一个测地全控制集,且基数至多为k′-1,矛盾.下面证明可找到一个不含 xu的测地全控制集D′.

若u∉D′且v∉D′,则必存在一个点 p∈D′使得pv∈E(G′).若p≠xv,那么在D′中用v代替 xu,仍得到G′的一个基数至多为k′测地全控制集;若p=xv,则在D′中用 u代替 xu,用 v代替 p(xv),仍得到G′的一个基数至多为k′测地全控制集.

若u∈D′,则对任意点 v∈NG(u)均有v∉D′,否则,D″=D′{xu}也是图G′的一个测地全控制集,且基数至多为k′-1,矛盾.那么在D′中用v代替xu,仍得到G′的一个基数至多为k′测地全控制集.因此可假设 xu∉D′.

令D=D′{yu,zu|u ∈V(G)}.因为 D′是 G′的一个全控制集,且对每个点u∈V(G)有NG(u)∩D≠φ,所以D是图G的一个全控制集,且|D|≤k′-2n=k.

[1]COCKAYNE E J,DAWES R M,HEDETNIEMI S T.Total domination in graphs[J].Networks,1980,10:211-219.

[2]HAYNES T W,HEDETNIEMI S M,HEDETNIEMI S T,et al.Domination in g raphs applied to electric power networks[J].SIAM J Discrete Mathematics,2002,15(4):519-529.

[3]乔 诚,王 勤.导出匹配可扩二部图度和条件的改进[J].中国计量学院学报,2010,21(1):75-77.

[4]王航平.图的Hamilton问题的着色否定方法[J].中国计量学院学报,2005,16(3):218-221.

[5]赵 敏.图的2-距离控制数为的必要条件[J].中国计量学院学报,2008,19(3):265-268.

[6]HAYNES T W,HEDETNIEM I S T,SLA TER P J.Fundamentals of domination in graphs[M].New York:Marcel Dekker,1998:299-325.

[7]HAYNES T W,HEDET NIEM I S T,SLATER P J.Domination in g raphs:advanced topics[M].New York:Marcel Dekker,1998:191-231.

[8]HA RARY F,LOUKAKIS E,TSOU ROS C.The geodetic number of a graph[J].Math Comput Modelling,1993,17:89-95.

[9]ESCUADRO H,GERA R,HANSBERG A,et al.Geodetic domination in graphs[EB/O L].[2010-12-20](2011-03-09).http://faculty.nps.edu/rgera/papers/geodom.final.pdf.

[10]HANSBERG A,VOLKMANN L.On the geodetic and geodetic domination numbers of a graph[J].Discrete M athematics,2010,310:2140-2146.

[11]ZWIERZCHOWSKI M.Total domination number of the conjunction of graphs[J].Discrete Mathematics,2007,307:1016-1020.

[12]DOU RADO M C,PROT TI F,RAUT ENBACH D,et al.Some remarks on the geodetic number of a graph[J].Discrete Mathematics,2010,310:832-837.

[13]LASKAR R C,PFAFF J,HEDETNIEMI S M,et al.On the algo rithmic complexity of total domination[J].SIAM J Algebraic Discrete M ethods,1984,5:420-425.