永磁磁共振成像装置主磁体设计方法研究
2011-11-20徐文龙徐冰俏陶贵生
李 霞,徐文龙,徐冰俏,陶贵生
(1.中国计量学院信息工程学院,浙江杭州310018;2.浙江大学 生仪学院,浙江杭州310027)
在(核)磁共振成像(NMR或MRI)装置中,样品被放置在一个静磁场中.在一个正比于静磁场的射频(Larmor频率)作用下,被测样品内的氢原子核发生共振.工作在Larmor频率下发射和接收线圈,去激励和接收来自氢原子核的磁共振信号.这些信号经过梯度线圈的空间编码和数字处理形成磁共振图像.因此,磁体为MRI中产生静磁场的关键装置[1].永磁主磁体是靠能够长时期地保持很强磁性的永磁材料来作为其磁场能源,由于永磁磁路不需要激磁线圈和供电系统,所以它的结构比较简单,也不耗电[2-4].
永磁主磁体主要由永磁磁极、极靴(极板和匀场环)和铁轭组成.永磁磁路主要采用电机中的磁路法进行设计.即将永磁机构分割为几个部分,引入磁阻和磁势的概念.这种方法能够解决问题的关键在于两点:第一,非常清楚待设计的永磁机构中的磁通走向,并且能分析主要因素和次要因素进行合适的简化;第二,通过简化和必要的分析,特别是根据实际的工程经验,能够计算出各部分的磁阻和相关的漏磁系数[5].在初始模型机构的基础上,采用现代数值计算方法,对模型进行计算,分析磁场的分布情况.本文以小动物成像仪为例,进行了主磁体结构设计和计算.
1 磁路方法
首先以一个双柱永磁结构来分析磁路法的设计.如图1为一个简单的双柱永磁磁路结构.
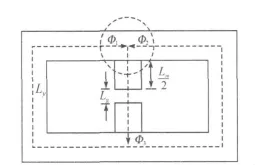
图1 双柱永磁磁路Figure 1 Two column permanent magnet curcuit
根据磁路的基尔霍夫定律[6],有
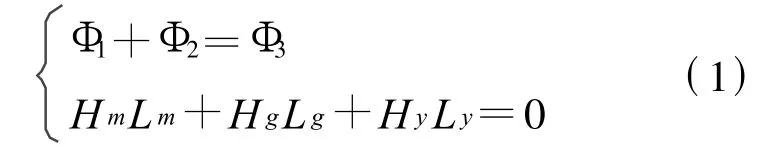
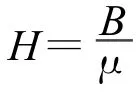
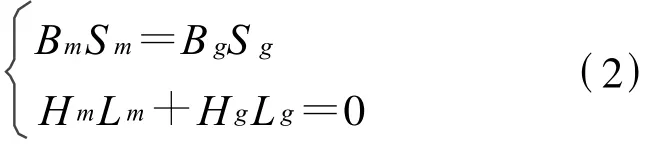
其中,Sm、Bm及Sg、Bg分别代表磁极和气隙的截面积和磁感应强度.如果已知磁路尺寸(Sm、Lm、Sg、Lg)以及磁性材料退磁曲线,可以求得
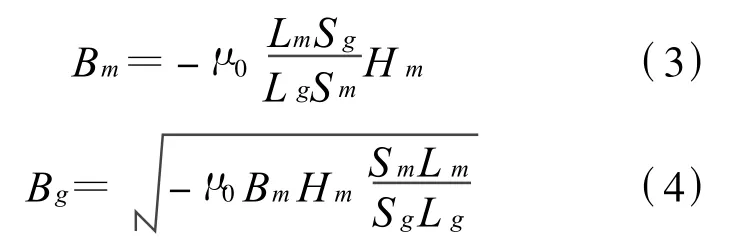
从式(3)可知Bm-Hm关系为一直线,常称之为工作负载线,磁路工作点既要在退磁曲线上又要在负载线上,故为两者的交点M,如图2,由此可得磁铁的Bm和Hm,代入式(4)即可求出工作气隙的磁感应强度Bg.
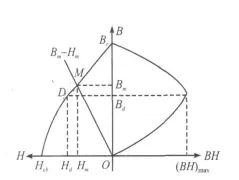
图2 永磁材料的退磁曲线与工作负载线Figure 2 Demagnetization curve and load line for permanent magnet materials
如果已知工作气隙尺寸及其磁感应强度(Sg、Lg、Bg),为提高永磁材料的利用率,通常将磁路工作点设计在最大磁能积处.退磁线上每点处B与H的乘积(BH)称为该点的磁能积,其中磁能积最大的点D称为最佳工作点,如图2.最佳工作点上的一般近似等于磁材的,其中 Br是剩磁,Hcb是磁感矫顽力,因此由式(3)可以得到
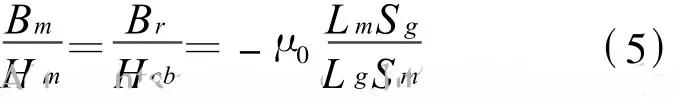
由式(2)和(5)可以求得磁铁的长度与截面积为
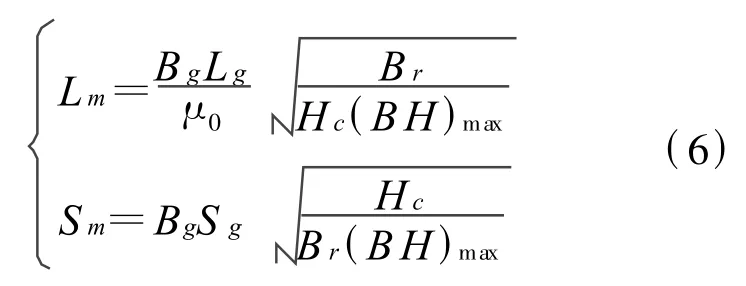
在磁路设计时必须考虑磁路漏磁情况及磁阻现象.这样,式(2)和式(6)应分别改写为
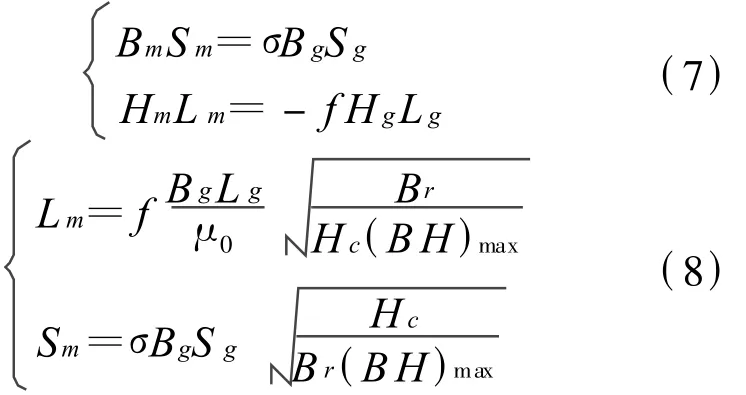
其中,f为磁阻系数,它与磁路尺寸、接合面积及工作间隙大小有关,σ为漏磁系数,它与磁路尺寸结构、材料属性等有关.
2 设计例子
通常情况下,MRI永磁体的磁极由 NdFeB材料制作,并设计成圆柱形,气隙也为圆柱形,铁轭用来支撑磁体构架并导通磁路,由A3钢做成,极靴由工业纯铁制作,用来平滑磁极表面,提高磁场均匀性.
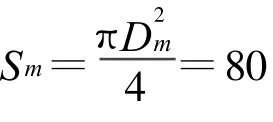
选取材料NdFeBN40,查阅N40磁材属性参数可知其剩磁Br=1.28 T,磁感矫顽力 Hc b=939.014 kA/m,最大磁能积(BH)max=300 kJ/m3.虽然工作气隙的横截面积和磁极的横截面积取为相等,但是需要根据经验公式计算出有效面积.对于圆形平面磁极,需要等效为正方形平面,并利用如下经验公式计算[8]:
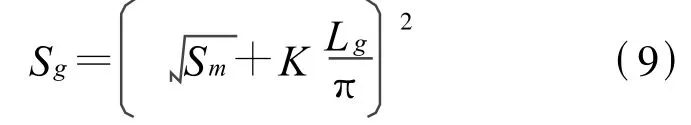
其中K为调节系数,它与磁极厚度和气隙的比值w(0.3≤w≤1.0)有关,本文取 K=0.5.于是得到
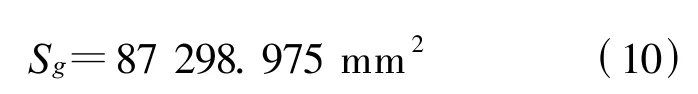
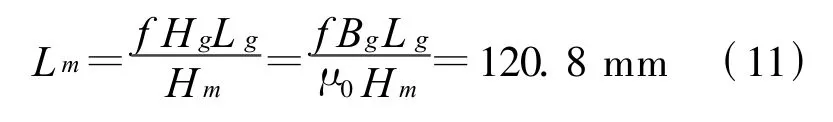
所以,上下磁极高度可以选为60.4 mm,本文选为62 mm.为了提高磁场均匀性,在磁极表面安装厚度25 mm的极板.
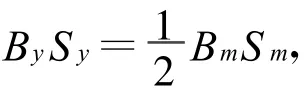
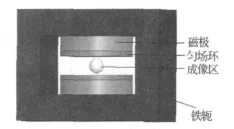
图3 磁体结构Figure 3 M agnet structure
3 有限元分析
借助磁路计算方法确定磁体结构的主要尺寸后,还通过数值计算方法可以得出其磁场分布情况.有限元方法是电磁场计算中广泛使用的一种数值计算方法[9-11].本文采用有限元商用软件Ansys进行了计算.
根据模型的对称性,采用Ansys对整个模型的1/8进行了2D和3D的磁场计算.2D磁力线分布及3D矢量分布分别如图4和图5.

计算得到磁体内的磁场分布的同时,还要计算成像区内的不均匀度.不均匀度的定义为:
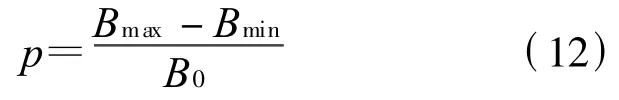
其中,Bmax、Bmin与B0分别为成像区内磁感应强度的最大值、最小值和中心点磁感应强度.本文计算出不均匀度为185.6×10-6,如果加入匀场环,则可以提高磁场均匀度.图6给出了加入匀场环后磁力线的分布情况.

图6 加入匀场环后的磁力线分布Figure 6 Distribution of magnetic field lines with shim ring
与图4比较,可以发现在图6中,气隙中的磁力线略向里鼓,成像区内的磁场均匀度会提高.所以,为了提高主磁场的均匀度,一般会从匀场环的优化设计入手.当然,得到匀场环的形状后,成像区内的磁场均匀度提高的同时,磁场强度会降低.本文采用Ansys软件进行了优化设计,当匀场环内径大约为外径的1/3时,得到成像区不均匀度为58×10-6.为了进一步提高磁场均匀度,实际还要经过匀场技术来达到目标参数要求.经过多次匀场和人工干预的方法进行调整后,均匀度可以达到25×10-6.
4 结 语
本文阐述了磁路设计方法的过程,并结合其他磁体结构的参数,针对小动物成像仪的参数要求,进行了设计.利用有限元方法对磁体结构进行了分析,并对匀场环的形状进行了优化计算,结果表明,设计的磁体满足成像要求.
[1]LI X,XIAL,CHEN W.Finite element analysis of gradient z-coil induced eddy currents in a permanent MRI magnet[J].Journal Magnetics Resonance,2011,208:148-155.
[2]MANZB,BENECHE M,VOLKE F.A simple small and low cost permanent magnet design to produce homogeneous magnetic fields[J].Journal Magnetics Resonance,2008,192:131-138.
[3]BAUERC,RAICHV H,JESCHKE G.Design of a permanent magnet with a mechanical sweep suitable for variabletemperature continuous-wave and pulsed EPR spectroscopy[J].Journal Magnetics Resonance,2009,198:222-227.
[4]陶贵生,李 霞,徐文龙.永磁磁共振系统盘式梯度线圈的设计[J].中国计量学院学报,2009,20(4):342-346.
[5]夏平畴.永磁机构[M].北京:北京工业大学出版社,2000:73-94.
[6]林其壬,赵佑民.磁路设计原理[M].北京:机械工业出版社,1987:85-92.
[7]徐 丹.核磁共振成像主磁体的设计及其优化[D].沈阳:沈阳工业大学,2009.
[8]武海澄.M RI磁体系统的计算机辅助设计研究[D].合肥:中国科学技术大学,2007.
[9]林鹤云.矢量磁位散度约束的罚函数方法中罚因子的数值特性[J].电工技术学报,1997,12(3):59-62.
[10]LI X,XIA L,LIUF.On the characterization and reduction of X-gradient induced eddy currents in a NdFeB M RI magnet-3D FEM-based numerical studies[J].Concepts in M agnetic Resonance B,2011,39B(1):47-58.
[11]谢德馨,杨仕友.工程电磁场数值分析与综合[M].北京:机械工业出版社,2008:77-127.
