控制力矩陀螺在天宫一号目标飞行器姿态控制上的应用

2011-11-25张志方董文强张锦江何英姿

空间控制技术与应用 2011年6期

关键词：构形角动量姿态控制

张志方，董文强，张锦江，何英姿

(1.北京控制工程研究所，北京100190;

2.空间智能控制技术重点实验室，北京100190)

控制力矩陀螺在天宫一号目标飞行器姿态控制上的应用

张志方1，2，董文强1，2，张锦江1，2，何英姿1，2

(1.北京控制工程研究所，北京100190;

2.空间智能控制技术重点实验室，北京100190)

根据天宫一号目标飞行器的特点及交会对接任务需求，天宫一号目标飞行器选择单框架控制力矩陀螺作为姿态控制执行机构，这是控制力矩陀螺首次在国内航天器上应用.阐述了单框架控制力矩陀螺在天宫一号目标飞行器姿态控制上的应用，主要包括四个方面:构形选择、操纵律设计、角动量却载、故障诊断与重构.天宫一号目标飞行器控制力矩陀螺系统采用五棱锥构形，其操纵律设计为带零运动的伪逆操纵律，控制力矩陀螺系统具备故障诊断和重构功能.

天宫一号目标飞行器;单框架控制力矩陀螺;姿态控制;操纵律

天宫一号目标飞行器是中国目前研制的航天器中体积最大、重量最重的航天器，作为对接目标，配合神舟八号飞船完成交会对接任务.根据任务特点，天宫一号目标飞行器的姿态控制既需要较大的控制力矩，又需要较高的姿态控制精度，喷气发动机、动量轮等姿态控制执行机构难以满足要求.参考“和平号”空间站、国际空间站的经验，采用控制力矩陀螺(CMG)作为控制执行机构可满足天宫一号目标飞行器的姿态控制需求.

根据框架的不同，控制力矩陀螺又可分为单框架(SG)和双框架(DG)两种.单框架控制力矩陀螺(SGCMG，single-gambal control moment gyro)系统虽然奇异现象严重，操纵律也比较复杂，但是具有机械结构简单、输出力矩大(力矩放大作用)等优点.而双框架控制力矩陀螺(DGCMG)则由于机械结构复杂，设计制造中硬件问题比较突出.天宫一号目标飞行器选择单框架控制力矩陀螺作为姿态控制执行机构，这是控制力矩陀螺首次在国内航天器上应用.

SGCMG由三部分组成，即高速转子、支撑转子的框架与实现框架期望运动的伺服系统.SGCMG在航天器中的应用主要考虑以下四个方面的问题:

(1)构形选择;

(2)操纵律设计;

(3)角动量卸载;

(4)故障诊断与重构.

以下分别从上述四个方面对SGCMG的应用进行阐述.

1 构形选择

SGCMG系统组成的基本要素有[1]:(1)SGCMG的数量;(2)SGCMG系统的构形;(3)SGCMG的角动量及最大的框架进动角速率.

在系统设计过程中，对SGCMG的数量和构形有以下要求:(1)SGCMG系统的角动量包络、输出力矩要满足系统任务所需的角动量和输出力矩要求.(2)在工作过程中，控制律及操纵律简单，尽可能回避内部奇异点，以免丧失三轴姿态控制性能.(3)SGCMG系统的可靠性要求:当某个SGCMG失效，SGCMG系统能够可靠检测故障、安全切换;当一个SGCMG失效，能够保持SGCMG系统的三轴

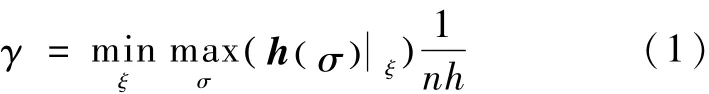
其中，ξ为由动量体中心指向包络的方向，n为SGCMG的数量，h()σ为SGCMG的角动量值，σ为SGCMG的框架角.

由于该指标没有考虑系统失效后的性能，为综合考虑构形的优劣，引入构形分析的另外一个指标——失效效益.

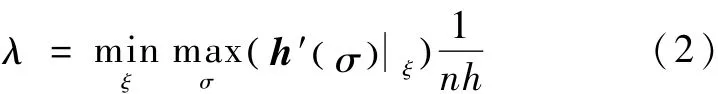
定义2(失效效益).在某一构形下的失效效益为SGCMG系统失效一个单框架控制力矩陀螺后的角动量包络上的最小角动量与失效前陀螺群角动量的代数和之比[1].控制性能;当两个 SGCMG失效，能够保持航天器的安全性.(4)在保证上述要求的基础上，尽可能减少SGCMG系统的数量，以减小系统的重量、功耗、体积、成本等.

常用的SGCMG系统的构形分为成对安装形式和非成对对称安装形式.通过对双平行构形、三平行构形、金字塔构形、四棱锥构形、五面锥构形和五棱锥构形等六种典型构形进行系统的分析，从构形效益、失效效益的对比等方面综合考虑，五棱锥构形6-SGCMG系统和金字塔构形的4-SGCMG系统是较为实用和有研究价值的形式.定义如下两种构形研究指标:

定义1(构形效益).在某一构形下的构形效益为SGCMG系统的动量包络上的最小角动量与陀螺群角动量的代数和之比[5].

其中，n为失效前SGCMG的数量，h′()σ为失效一个后SGCMG的动量值.

对于金字塔构形，其安装方式如图1所示.

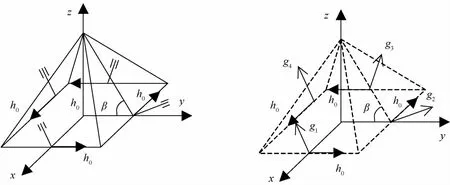
图1 金字塔构形安装方式图

对于五棱锥构形，其安装方式如图2所示.

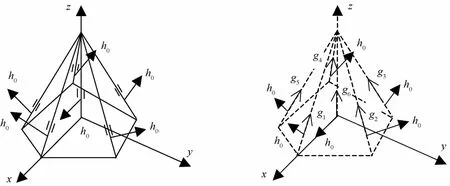
图2 五棱锥构形安装方式图

根据分析，得到两种典型构形的构形效益、失效效益，如表1所示.

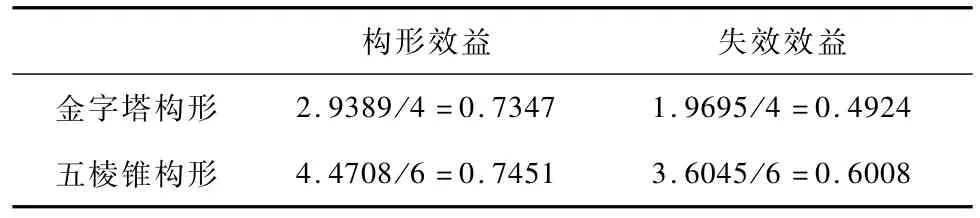
表1 两种典型构形的对比表

对于SGCMG系统的构形，有如下结论:

1)一般来说，对于成对安装形式和非成对对称安装形式，随着SGCMG数量的增加，系统的构形效率增加，而奇异面的复杂程度随之增加，增加了操纵律设计的困难.

2)在选择 SGCMG的数量相同的情况下，SGCMG系统的构形中成对安装形式相比较非成对对称安装形式的各种构形效益都略低，但是其奇异面的复杂程度较小，操纵方便.

3)考虑综合因素，对于长寿命低轨道的航天器，6-SGCMG系统的五棱锥构形是单框架力矩陀螺的最佳构形.就研究本身而言，以金字塔构形的4-SGCMG作为分析对象，具有深远意义，该构形具有一定的代表性，对此种构形的奇异分析和操纵研究，有助于为更多数SGCMG系统的奇异分析和操纵提供指导.

2 操纵律设计

SGCMG姿态控制回路如图3所示，SGCMG姿态控制回路由航天器动力学、姿态测量、SGCMG控制律与操纵律、SGCMG卸载律、SGCMG系统动力学组成.系统设计中需设计和解决SGCMG姿态控制律、SGCMG操纵律、SGCMG卸载律等问题.

SGCMG主要用于天宫一号目标飞行器在长期在轨运行期间克服各种内外干扰力矩，保持姿态稳定.以SGCMG为执行机构控制航天器姿态，在中国航天领域是一种全新的方式，没有任何飞行经验可以借鉴.天宫一号目标飞行器的姿态控制律采用经典控制理论进行设计.SGCMG系统的操纵律和卸载律是SGCMG系统姿态控制设计的难点所在.

SGCMG系统的合成角动量可表达成:

其中h0为SGCMG转子标称角动量，A、B为SGCMG的安装矩阵(均为3×6矩阵)，仅与安装有关.

Sσ，Cσ为框架角正、余弦对角阵(均为6×6矩阵):

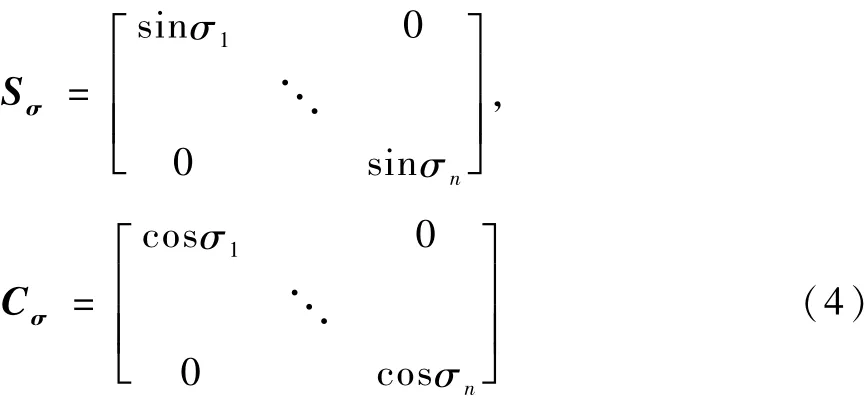
E为 n 维单位矢量，E=(1，1，…，1)T.

J=(ACσ-BSσ)称为 SGCMG系统的雅可比阵.

SGCMG操纵律的设计是寻求当任意给定SGCMG系统的期望输出力矩，，根据SGCMG系统的操纵律能够找到¯，作用于SGCMG系统，使得SGCMG系统的框架角轨迹满足()=0并且尽可能满足J()满秩.其中:为SGCMG系统的控制力矩，(）=h0J()为 SGCMG系统的输出力矩，J()为 SGCMG系统的雅可比阵，为 SGCMG系统的框架角速度.

根据求解方式，SGCMG系统的操纵律可分为框架角操纵律、框架角速率操纵律和框架角加速度操纵律[2].对于框架角速率操纵律，主要有三种形式:(1)Penrose-Moore伪逆操纵律.(2)带零运动的伪逆操纵律，具有零运动的伪逆方法是通过零运动改变SGCMG系统的雅可比矩阵，以改变奇异状态的出现.(3)奇异鲁棒(S-R)逆操纵律.目前已知用于实际的SGCMG系统操纵律是“和平号”空间站的操纵律，使用的是带零运动的伪逆操纵律.

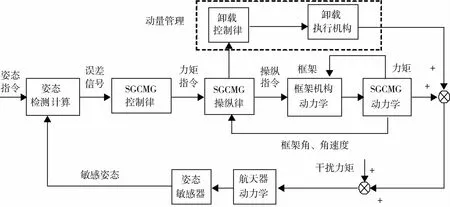
图3 SGCMG姿态控制回路示意图

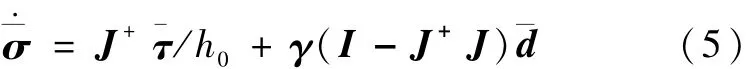
其中:J+=JT(JJT)-1为 Penrose-Moore伪逆，I为适当维数的单位阵，γ，¯d 为零运动参数.对于 γ，的选择有各种各样的形式，得到回避奇异状态的性能也略有不同.

“和平号”空间站的SGCMG系统操纵律采用了具有投影矩阵形式的零运动伪逆方法[3].

具体的形式为:

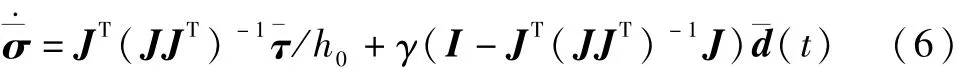
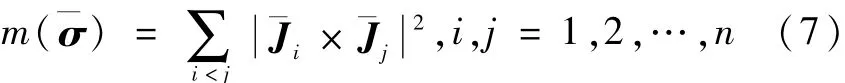
天宫一号目标飞行器SGCMG系统的操纵律在借鉴“和平号”空间站操纵律基础上，对奇异测度函数m()进行了重新定义，设计带零运动的鲁棒伪逆操纵律，该操纵律可避免求逆运算溢出、框架“锁死”，在奇异点处仍有可控性.当框架构形接近奇异时，通过零运动及添加小量力矩误差，使框架尽快脱离奇异状态;在非奇异处，不需要使用零运动回避奇异，令零运动项为零，同时令鲁棒伪逆权系数为零，则鲁棒伪逆与一般伪逆等同，无力矩误差，系统实现精确控制.

3 角动量卸载

由于外干扰力矩的作用，SGCMG系统角动量不断积累，如果角动量积累达到其饱和容量，则SGCMG系统不能产生期望的输出力矩，SGCMG失去姿态控制能力.因此必须对SGCMG系统进行角动量卸载.一般采用喷气卸载、磁力矩器卸载等.喷气卸载虽然简单有效，但其中工作燃料的消耗及对航天器带来的污染却是不可忽视的.磁力矩器卸载虽然不需工作燃料的消耗，但需要精确的地磁场模型和相应的硬件设备，给敏感器件带来了磁污染.

3.1 喷气卸载

当SGCMG系统合成角动量达到饱和状态或SGCMG系统进入奇异状态，需要进行喷气卸载，即当前姿态控制方式转为喷气控制，SGCMG系统开始角动量卸载，当SGCMG系统合成角动量达到标称值(零动量)附近时卸载完毕，当姿态满足转 CMG控制条件时则转入CMG控制.

SGCMG系统角动量卸载有两种方式:方式一，使各SGCMG框架角回到指定的初始位置，在该框架角组合下SGCMG系统角动量为零，奇异值较大;方式二，通过给SGCMG系统施加指定控制力矩指令使SGCMG系统朝角动量减小的方向运动，直到系统角动量减小到零动量附近，达到卸载目的，该方式下框架角并不回到初始位置.

3.2 磁力矩器卸载

SGCMG系统在控制航天器姿态时，吸收外扰动力矩而使其合成角动量偏离标称值，磁力矩器卸载(以下简称磁卸载)是利用航天器产生的合适磁距与地磁场作用来减小控制力矩陀螺系统的合成角动量，使其角动量保持在较小的阈值范围内.

磁卸载是在SGCMG系统正常姿态控制过程中利用磁控系统对SGCMG系统不断累积的角动量实时卸载，其原理如下:

地磁场强度B由轨道计算得到，SGCMG系统角动量ΔH由控制计算机采集SGCMG系统框架角及高速转子转速信息计算得到.记磁力矩器产生的磁矩为M，磁卸载力矩为TM，一般采用叉乘规律产生磁距[4]:

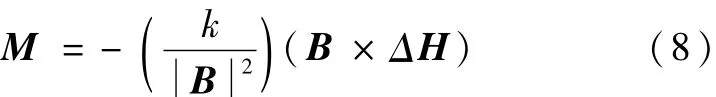
此处，k＞0是增益系数，则作用在航天器上的力矩为:

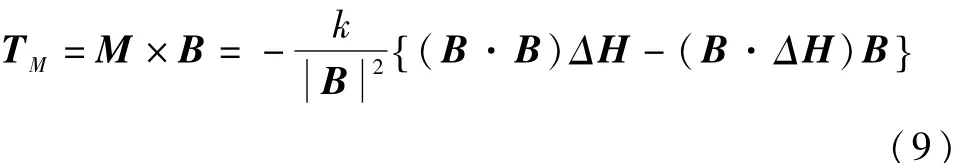
当B⊥ΔH时，则 TM=-kΔH，可知磁力矩总是使积累的角动量减少.当B不垂直ΔH时，为了限制不利部分，一般要求|b·Δh|＜ε(ε为设计可选的阈值)时才进行磁卸载，b与Δh分别为 B与 ΔH方向的单位矢量.

4 故障诊断与重构

姿态控制系统的故障诊断一般分两级进行:一是部件级自检，它提供部件工况及数据的有效性等信息;二是由系统方面进行检测，主要利用相关量信息的一致性以及执行效果与期望值进行比较等进行诊断，考虑的因素较多，需要一定时间.部件故障诊断由部件自检及系统检测相结合进行.

SGCMG系统故障定位可以由星上自主故障诊断及地面通过遥测信息判断获得，当SGCMG系统出现故障时需要进行SGCMG系统重构，在控制系统设计时在SGCMG选型、姿态控制等多个方面都充分考虑了SGCMG系统重构设计.对SGCMG系统具体工程应用，要求在一部分SGCMG出现故障时，具有一定的可容性，SGCMG系统仍能保持适当的工作性能，能够产生输出力矩对航天器姿态进行控制，达到这一目标的前提是能够诊断并定位SGCMG系统的故障并对其他 SGCMG进行重构，对故障的SGCMG断电，使其滑行减速.根据对动量轮故障诊断的经验，采用基于力学原理方法对SGCMG进行诊断与定位.

当SGCMG系统某一个或几个出现故障，剩余的SGCMG系统组成新的系统，其角动量包络、奇异面的形状和特性都发生了相应的变化，而且回避奇异、动量管理问题也更加严重和突出.解决的方法有两个方面，一方面是在 SGCMG系统的组成上，对SGCMG的数量和构形进行分析，在保证冗余的前提下，得到最佳的SGCMG的组成选择.另一方面是从系统软件实现方面考虑故障的判断、检测和相应的控制律的切换.

在控制器设计时选择具有一定自适应能力的控制器，在一个或二个 SGCMG出现故障后，SGCMG的操纵律和卸载律无需作大的变化，只需在操纵律中，将故障SGCMG产生控制力矩的相关项剔除，其余的SGCMG系统(由未故障的SGCMG组成)自动进行重构，产生输出力矩控制航天器姿态.

5 姿态机动及数学仿真

天宫一号目标飞行器轨道高度约350km，轨道倾角约42°，质量约8500kg.在天宫一号目标飞行器三轴对地飞行过程中，空间环境干扰力矩(气动力矩、重力梯度力矩、剩磁力矩、太阳光压力矩)相对较小，姿态控制所需的控制力矩较小，SGCMG框架角短时间内基本保持不变，在磁卸载的作用下，角动量能完全卸载，不存在角动量饱和问题.由于框架角短时间内基本保持不变，因此也不易陷入奇异.在姿态机动期间，SGCMG系统角动量、框架角变化范围均较大，框架构形容易接近奇异状态.对SGCMG控制律及操纵律的考核主要体现在姿态机动性能上，要求使用六个SGCMG及五个SGCMG(假定失效一个)均能完成所有姿态机动任务，姿态机动期间要考虑SGCMG所能提供的控制力矩、角动量容量限制、奇异回避、姿态控制精度约束、机动时间约束等问题.本文主要对天宫一号目标飞行器姿态机动过程进行分析.

天宫一号目标飞行器的姿态机动主要有如下两个方面:

(1)偏航180°姿态机动

偏航180°姿态机动主要用于降轨前后的调姿以及在偏航180°状态下配合飞船进行交会对接.

(2)连续偏航机动

记太阳矢量(由目标飞行器指向太阳方位的单位矢量)与轨道面夹角为βn，天宫一号目标飞行器采用单自由度太阳电池翼，三轴对地姿态下太阳电池翼平面法线与太阳矢量的最小夹角即为βn.对于天宫一号目标飞行器的运行轨道，βn变化范围较大，当βn大于一定角度后，能源供应不足，可采用偏航机动的方法解决该问题，通过机动合适的偏航角度ψr，再驱动太阳电池翼到合适方位，可实现太阳电池翼平面法线完全对准太阳.由于太阳方位相对目标飞行器缓慢变化，所需的偏航机动角度ψr也随之变化，目标飞行器处于连续偏航机动状态.

5.1 姿态机动控制律设计

对于大角度的姿态机动，一般采用跟踪期望轨迹的方法实现.

针对偏航180°姿态机动，考虑到 SGCMG系统的最大角动量包络限制，姿态机动时必须限制最大机动角速度，因此将机动过程规划为加速、匀速、减速三段，规划出的姿态角速度及姿态角如图4所示:

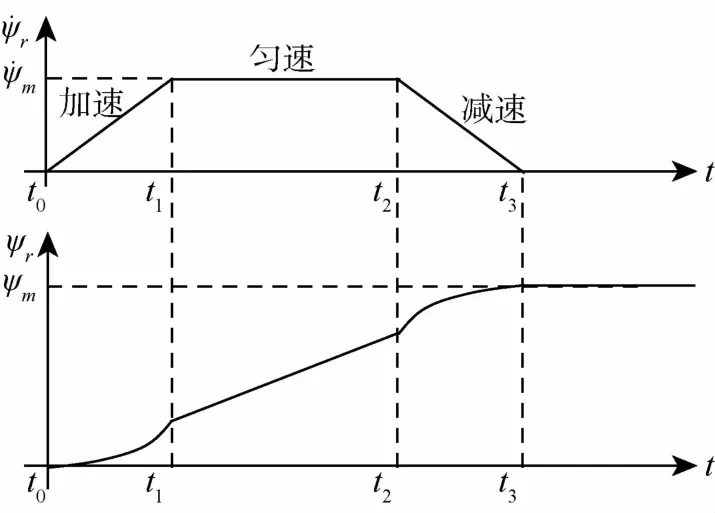
图4 偏航机动轨迹示意图

图中t0为姿态机动起始时刻，t1为姿态机动加速结束时刻，t2为匀速运动结束时刻，t3为机动结束时刻.

采用匀加速、匀减速方式，根据机动过程的控制力矩、时间约束合理设定机动角加速度 am，根据角动量最大允许值设定最大机动角速度˙ψm，则加速段时间、减速段时间、匀速段时间均可得到.

加速段时间tα为:

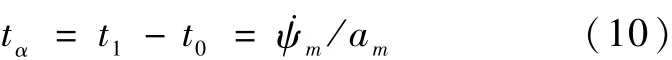
匀速段时间tβ为:

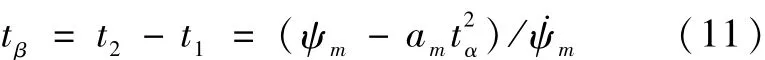
根据姿态机动角加速度am、机动角速度˙ψm、加速段时间tα、匀速段时间 tβ即可规划姿态机动过程的目标姿态角ψr及目标姿态角速度˙ψr.

姿态机动采用PD控制，为减小跟踪误差，提高跟踪精度，在加速段及减速段增加前馈补偿，补偿力矩如下:

其中Ib为天宫一号目标飞行器惯量矩阵，Abr为本体系相对参考系的方向余弦矩阵，˙ωri为参考系相对于惯性系的角加速度，Tb即为所需的前馈补偿力矩.

针对天宫一号目标飞行器连续偏航机动，根据太阳矢量(记太阳矢量在轨道系的表示为[Sox，Soy，Soz]′)在目标飞行器轨道系的变化规律，偏航机动目标姿态角及目标姿态角速度是确定的，其中偏航机动目标姿态角ψr为:

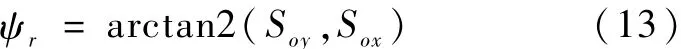
对ψr求导即可得到偏航机动目标角速度˙ψr及目标角加速度¨ψr.由于天宫一号目标飞行器处于连续偏航机动过程中，因此其角动量呈现周期性波动，最大角动量取决于偏航机动目标角速度˙ψr及目标飞行器偏航轴的惯量.在SGCMG角度量容量选择时，已考虑到偏航机动的需求，角动量包络大于偏航机动期间角度量波动范围.

连续偏航机动采用PID控制，为提高姿态机动跟踪精度，增加形如式(12)的前馈补偿力矩.

5.2 数学仿真

以天宫一号目标飞行器为对象进行数学仿真，仿真条件:轨道高度 350km，轨道倾角 42°，质量8500kg.以下分别进行了六个 SGCMG以及五个SGCMG(假定一个失效)的姿态机动仿真.

图5～图7为采用六个 SGCMG偏航180°姿态机动的仿真曲线，图8～图10为采用六个 SGCMG连续偏航机动的仿真曲线，图11～图13为采用五个SGCMG偏航180°姿态机动的仿真曲线，图14～图16为采用五个SGCMG连续偏航机动的仿真曲线.受角动量容量限制，使用6个SGCMG偏航180°姿态机动时角速度限制设计为0.4(°)/s，使用5个SGCMG偏航180°姿态机动时角速度限制设计为0.3(°)/s，均能满足实际应用需求.

目标飞行器实际在轨飞行时多次进行偏航180°姿态机动及连续偏航机动，飞行结果与数学仿真结果相近，在姿态机动过程中均由 SGCMG进行姿态控制，SGCMG系统角动量未饱和、也未陷入奇异.数学仿真及实际飞行结果均表明，对于五棱锥构形及带零运动的鲁棒伪逆操纵律，在一个 SGCMG失效时，仍具有较好的操控性.

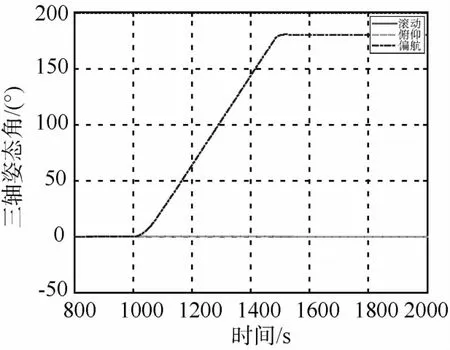
图5 偏航180°姿态机动过程姿态角变化曲线(六个SGCMG)

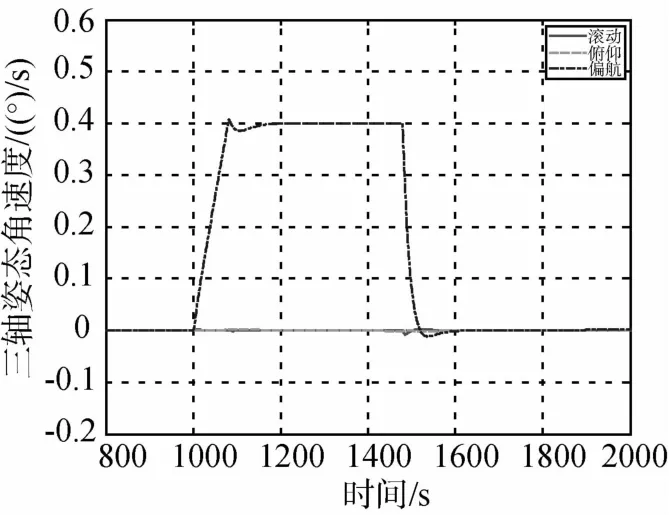
图6 偏航180°姿态机动过程姿态角速度变化曲线(六个SGCMG)

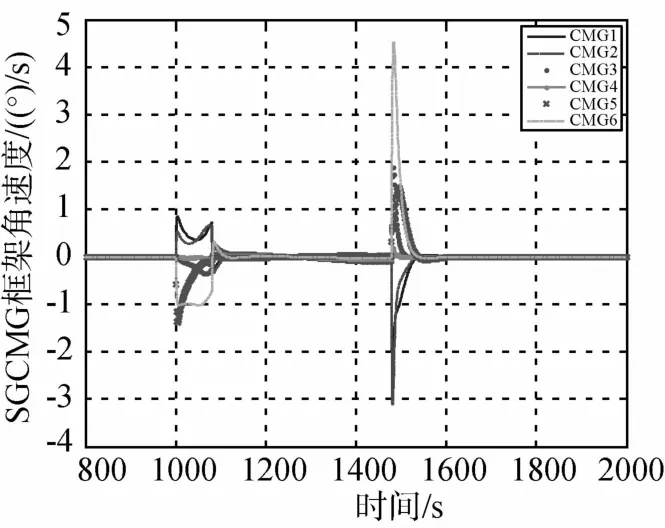
图7 偏航180°姿态机动过程SGCMG框架角速度变化曲线(六个SGCMG)

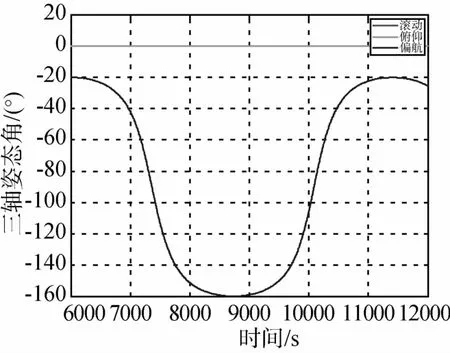
图8 连续偏航机动姿态角变化曲线(六个SGCMG)

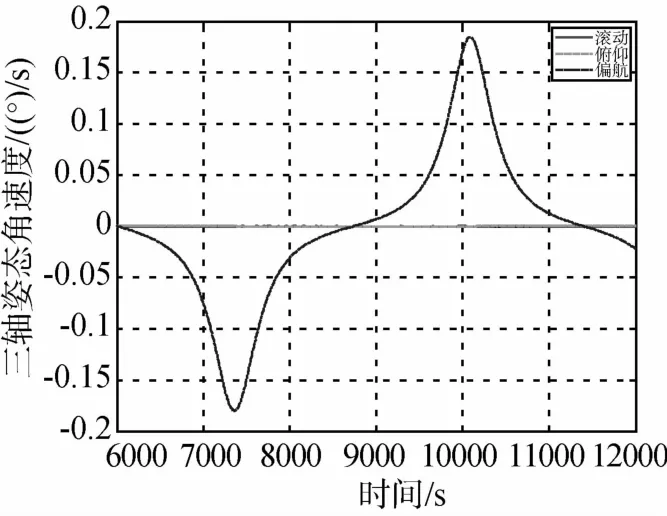
图9 连续偏航机动姿态角速度变化曲线(六个SGCMG)

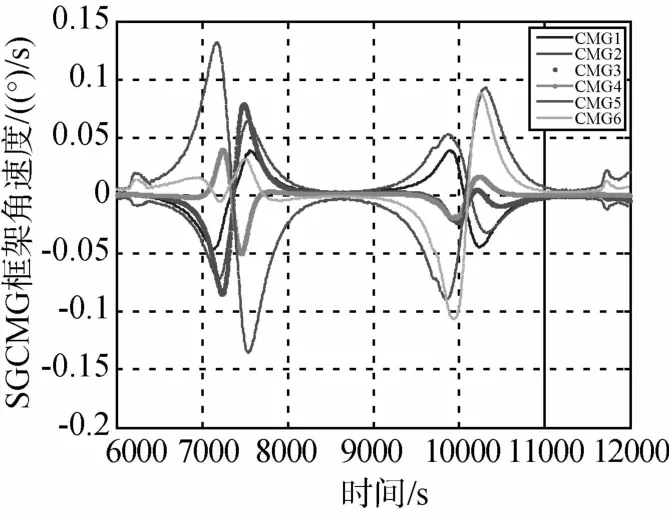
图10 连续偏航机动SGCMG框架角速度变化曲线(六个SGCMG)

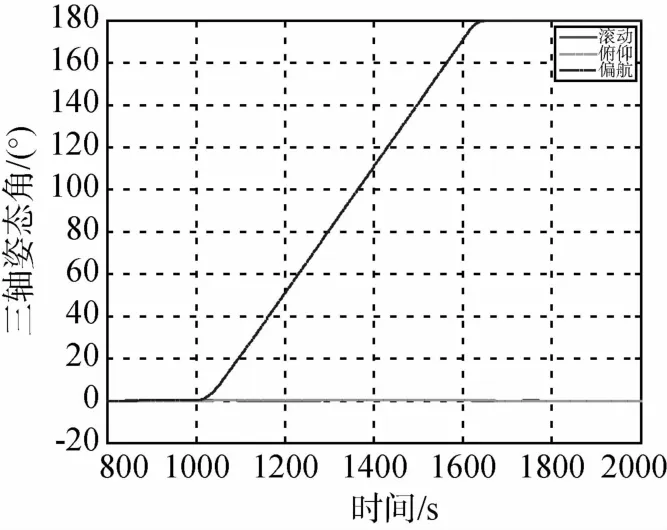
图11 偏航180°姿态机动过程姿态角变化曲线(五个SGCMG)

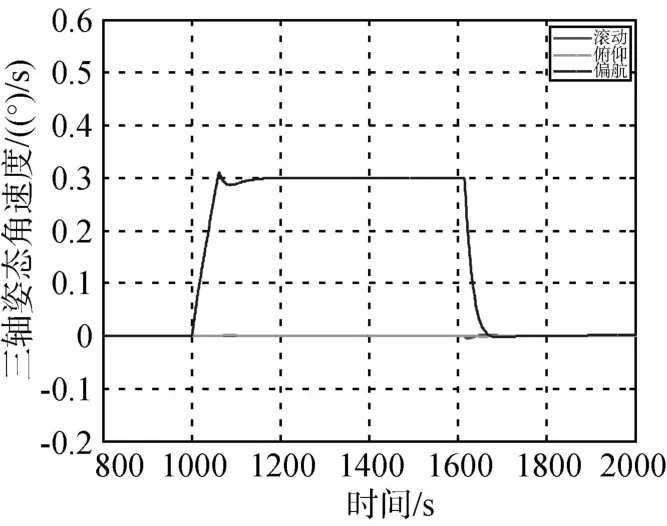
图12 偏航180°姿态机动过程姿态角速度变化曲线(五个SGCMG)

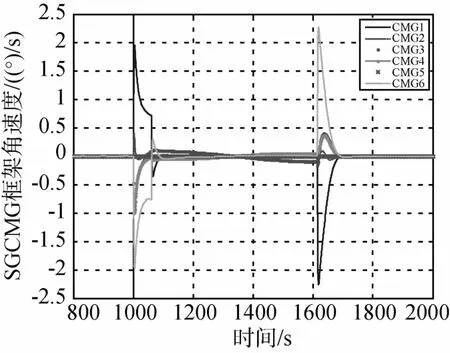
图13 偏航180°姿态机动过程SGCMG框架角速度变化曲线(五个SGCMG)

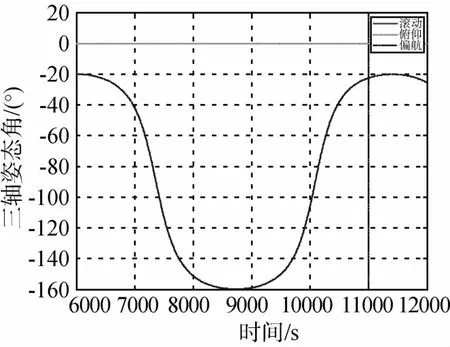
图14 连续偏航机动姿态角变化曲线(五个SGCMG)

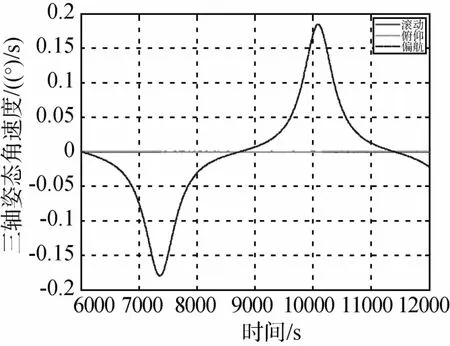
图15 连续偏航机动姿态角速度变化曲线(五个SGCMG)

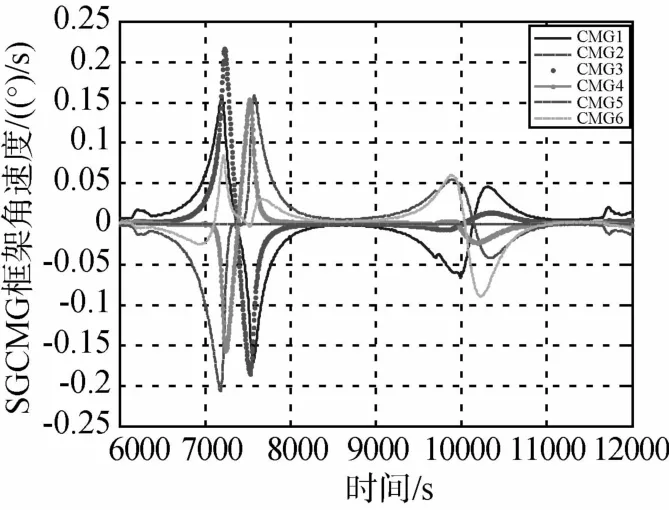
图16 连续偏航机动SGCMG框架角速度变化曲线(五个SGCMG)

6 结束语

本文从SGCMG系统的构形选择、操纵律设计、角动量卸载、故障诊断与重构四个方面对单框架控制力矩陀螺在天宫一号目标飞行器上的应用进行了阐述.随着航天器的性能要求越来越高，对于具有特殊需求(例如高精度的地球观测、空间观测，快速机动)的航天器，控制力矩陀螺的应用将会更加广泛.单框架控制力矩陀螺在天宫一号目标飞行器上的成功应用将为SGCMG在中国空间站的设计与应用打下良好的基础.

[1] 张锦江.单框架控制力矩陀螺系统的构形分析和对比研究[J].中国空间科学技术，2003，23(3):52-56

[2] 吴忠，吴宏鑫.单框架控制力矩陀螺系统操纵律研究综述[J].宇航学报，2000，10(4):140-145

[3] 吴忠，吴宏鑫.“和平号”空间站 SGCMG系统及其操纵[J].航天控制，1999，17(2):76-80

[4] 屠善澄.卫星姿态动力学与控制[M].北京:宇航出版社，2001

[5] 章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版，1998

[6] 张锦江.SGCMG系统的奇异状态脱离性判定方法研究[J].中国空间科学技术，2001，21(4):21-25

[7] 汤亮，贾英宏，徐世杰.使用单框架控制力矩陀螺的空间站姿态控制系统建模与仿真[J].宇航学报，2003，24(2):126-131

[8] Bedrossian N S.Steering law design for redundant single-gimbal control moment gyroscopes[J].Journal of Guidance， Control and Dynamics， 1990， 13(6):1083-1089

The App lication of Control M om ent Gyro in Attitude Control of Tiangong-1 Spacecraft

ZHANG Zhifang1，2，DONGWenqiang1，2，ZHANG Jinjiang1，2，HE Yingzi1，2
(1.Beijing Institute of Control Engineering， Beijing 100190，China;2.Science and Technology on Space Intelligent Control Laboratory，Beijing 100190，China)

According to the characteristics of Tiangong-1 spacecraft and the demand for rendezvous and docking mission，the single-gambal control moment gyro is used as the attitude control actuator of Tiangong-1 spacecraft.This is the first application of controlmoment gyro in the domestic spacecraft.The application of the controlmoment gyro in Tiangong-1 spacecraft is presented in this paper，which mainly includes 4 aspects:configuration， steering law， angular momentum unloading and fault diagnosis and reconfiguration.The configuration adopted by the controlmoment gyro system of Tiangong-1 spacecraft is the pentagonal pyram id configuration.The pseudo inverse steering law with zero motion is adopted.The fault diagnosis and reconfiguration is designed for the controlmoment gyro system.

Tiangong-1 spacecraft;single-gambal controlmoment gyro;attitude control;steering law