基于交会对接CCD光学成像敏感器的双目测量算法

2011-11-25涂俊峰管乐鑫解永春

空间控制技术与应用 2011年6期

关键词：光点双目交会

张昊，石磊，涂俊峰，管乐鑫，解永春

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

基于交会对接CCD光学成像敏感器的双目测量算法

张昊1，2，石磊1，2，涂俊峰1，2，管乐鑫1，2，解永春1，2

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

在空间交会对接近距离逼近阶段，CCD光学成像敏感器作为相对导航信息获取的主要测量敏感器，其测量性能直接关系到空间交会对接能否成功.针对适用于空间交会对接过程中CCD光学成像敏感器的双目测量算法展开研究，推导了基于主像机坐标系的双目测量算法计算公式，并重点对其抗干扰能力进行研究，最后对该双目测量算法进行了仿真分析并给出了仿真结果.

交会对接;CCD成像敏感器;双目测量算法;抗干扰

随着载人航天技术的不断发展，空间交会对接技术已经开始向着自主自动交会对接，必要时辅以地面遥控这一方向发展[1].对于自主自动的交会对接，根据交会对接不同的阶段划分和不同的导航信息需求，通常采用不同的导航敏感器.在最后逼近阶段，一般采用CCD光学成像敏感器做为主要的导航敏感器，以获取两个航天器的相对位置和相对姿态导航信息.

CCD光学成像敏感器的工作原理是根据二维成像信息还原得到三维位置姿态信息，当光点数和光点布局满足一定条件且光点在目标标志器上的安装位置已知、通过像机成像可以提取到像点在像机坐标系下的坐标时，采用一定的测量算法可以求解得到目标标志器与CCD像机之间的相对位置和相对姿态[2].在单像机测量方案中，目前多采用迭代算法，其优点是抗噪能力强，但缺点是需迭代求解计算量大[3].而双像机测量方案，由于增加了测量信息，可采用解析算法求解，计算量较小.本文在总结前人研究的基础上[4-5]，针对适用于空间交会对接过程中CCD光学成像敏感器的双目测量算法展开研究，推导了基于主像机坐标系的双目测量算法计算公式，并重点对其抗干扰能力进行研究，最后对该双目测量算法进行了仿真分析并给出了仿真结果.

对于在轨航天任务，若配备了两台CCD光学成像敏感器，且都工作正常，可采用本文给出基于主像机坐标系的双目测量算法计算相对状态，当备像机出现故障时，可采用主像机单目迭代测量算法求解，从而实现故障情况下测量数据的平稳过渡.

1 CCD成像敏感器的测量原理

CCD光学成像敏感器单个像机测量的基本原理是:

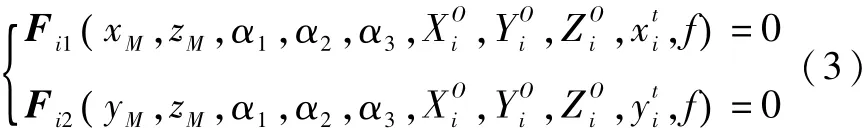
最后通过测量算法对N个光点组成的测量方程组求解，即可得到标志器坐标系与像机坐标系之间的相对姿态旋转矩阵C和相对位置M.

2 基于主像机坐标系的双目测量算法

本文第一节给出了交会对接CCD光学成像敏感器单像机测量算法，当像机数量多于1个时，通过不同像机对多个特征光点成像，可以通过解析方法求得标志器坐标系相对于像机坐标系的相对位置和相对姿态.下面以两像机为例，推导基于主像机坐标系的双目测量算法的基本方程.

2.1 计算方法

1个像机坐标系的姿态旋转矩阵，MC2{C1}≜为第2个像机坐标系原点在第1个像机坐标系下的坐标，C{C2}{C1}、MC2{C1}可由两个像机的安装方位和安装位置确定.

由测量原理可知第i个光点在两个像机坐标系下的坐标分别为:

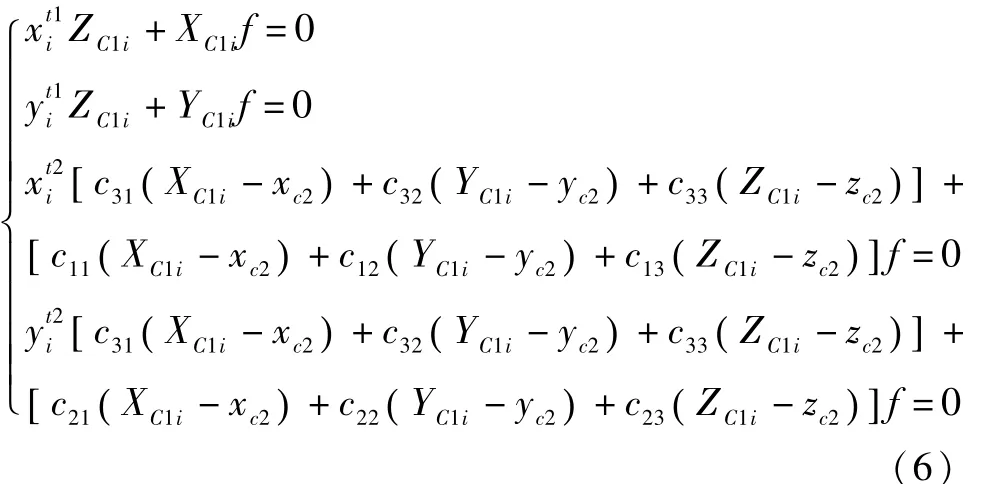
r1=(ATA)-1ATB (7)

由式(7)即可得到第i个光点在第1个像机坐标系下的准确坐标.当求出全部N个光点在主像机坐标系下的坐标后，由于光点在目标标志器下的安装位置已知，通过多矢量定姿即可得到目标标志器相对于主像机坐标系的相对姿态，具体计算方法如下:

对于全部N个光点分别满足测量原理式(1)，消去MT{C}可得:

U=C{C}{T}V或改写为:定义 1[8].设 A∈Rm×n，秩()A=r，对 A进行满秩分解 A=BC，B∈Rm×r为列满秩矩阵，C∈Rr×n为行满秩矩阵，定义广义逆矩阵为:

由范数定理可知[8]，式(9)的范数最小解为:

由于所有光点不共线，因此观测矢量矩阵U的秩为2或3.

1)若矩阵U的秩为3:此时矩阵U为行满秩矩阵，可取定义1中的矩阵B=I，C=U，此时U+=UT代入式(10)可得

一般情况下，通过式(11)求解得到的相对姿态矩阵 C{T}{C}为非正交矩阵，若直接将姿态矩阵C{T}{C}正交化，则又不满足观测方程式(9)，因此可将观测矢量误差阵ΔU作为优化极值指标，在最优化情况下对姿态矩阵C{T}{C}正交化，最终可得相对姿态矩阵C{T}{C}的最优解为:

其中，C{T}{C}由式(12)确定.

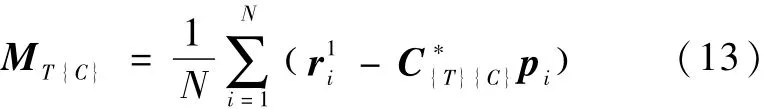
2)若矩阵U的秩为2:此时全部光点共面，利用双矢量定姿的相关原理，可以引入与平面垂直的法线矢量作为辅助测量，即在参考矢量矩阵V中增加列向量:在观测矢量矩阵U相应的增加列向量:

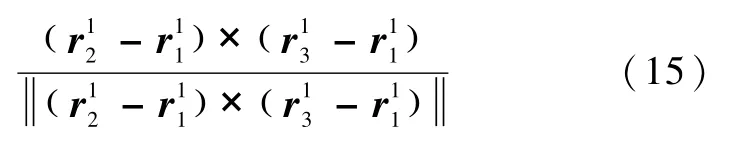
由此得到的新的观测矢量阵U为行满秩矩阵，进而可利用式(11)～(13)求解相对姿态旋转矩阵和相对位置.

综上所述，通过式(7)、(11)～(13)可得到完整的基于主像机坐标系的CCD光学成像敏感器双目测量算法.

2.2 抗干扰分析

由2.1节双目测量算法的基本计算公式可知，求解每个光点在第1个像机(主像机)坐标系下的位置坐标是双目测量算法的求解关键，因此在本节的抗干扰分析中，重点研究当存在测量偏差，特别是像点提取偏差时，求解每个光点在主像机坐标系下位置坐标的精度.

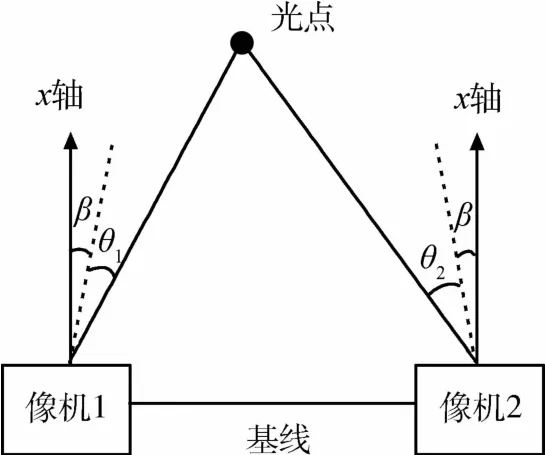
图1 两像机安装位置俯视图

图1所示的是双目像机的安装位置俯视示意图，由于两个CCD像机同时对一个目标标志器成像，因此在安装时需要一定的安装倾角β以保证视场要求，图中坐标系为追踪航天器本体坐标系，虚线表示像机光轴，设光点在主像机坐标系下的坐标为其在两个像机坐标系下的像点坐标分别为并且与两个像机的光轴张角分别为 θ1、θ2，简化的几何关系如图 2所示.

图2 双目测量简化几何关系示意图

由图2所示的几何关系可得:

将式(16a)代入式(16c)可得:

其中，A1=b sinβtan(θ2+2β)+b cosβ，B1=tan(θ2+2β)+tanθ1.

将式(17)代入式(16a)可得:

对于光点的y坐标存在如下关系:将 XC1，YC1，ZC1分别对求偏导数

可得:

假设两个CCD像机的像点提取偏差为则由误差传递公式可知:

将式(20)～(22)代入式(23)和式(24)即可得到光点在主像机坐标系下的位置精度.

通过上述分析可知，由双目算法解算出的测量信息的精度主要取决于如下4种因素:

(1)误差源的大小:误差源是导致测量信息产生误差的根本原因，减小误差源大小可以有效提高双目算法的测量精度;

(2)像机焦距f:测量误差大小与CCD像机焦距f成反比，即增大像机焦距可以提高双目算法的测量精度;

(3)基线长度b:双目算法中的基线长度通常是指两个像机之间的安装距离，当误差源大小和像机焦距一定时，增大基线长度也可以有效提高双目算法的测量精度;

(4)纵向测量距离(近似等于ZC1):测量误差大小与纵向测量距离成正比，当纵向距离距离较远时，双目算法的测量误差较大.

在工程应用时，由于安装工艺、像机性能以及敏感器测量范围相对确定，即测量误差源大小、像机焦距以及纵向测量距离一定，此时采用双目算法获得的测量精度主要取决于基线长度，需要针对具体情况对测量精度进行分析.

2.3 仿真分析

仿真条件为:

1)CCD像机性能及安装:像机焦距为0.028m，像机视场为 24°(全角)×24°(全角)的方形视场，测量范围0～30m，在双目测量算法仿真中，像机1的安装倾角β为2°，像机2的安装倾角β为 -2°，两像机安装距离为0.3m;

2)光点布局尺寸:五光点立体对称布局，标志器半径0.3m，突出光点高度0.2m;

3)测量误差源:a)无其他测量误差;b)1号光点存在1mm安装偏差;c)像点提取存在1μm(3σ)随机误差.

下面在敏感器测量范围内15361个不同的相对位置和相对姿态仿真点处(每512点为纵向距离1m)，针对上述3种误差源，采用双目测量算法进行了仿真分析，仿真结果如下.

图3 无测量误差(只有测量算法解算误差)的测量算法解算误差仿真曲线

图4 1号光点存在1mm安装偏差情况下的测量算法解算误差仿真曲线

由上述仿真结果可以得到如下几点结论:

1)当不考虑其他测量误差源，只有测量算法的解算误差时，双目测量算法的解算精度较高，位置精度在10-12m以上量级，姿态角精度在10-10(°)以上量级，算法精度满足要求;

2)当存在像点提取误差时，双目测量算法的位置解算误差可以满足精度要求，但姿态角解算误差较差，且解算误差与误差源大小、像机焦距、纵向测量距离和基线长度均有关，当误差源大小、像机焦距和纵向测量距离一定时，增大基线长度可以有效降低解算误差，但基线长度的增大需要考虑实际安装情况;

3)当目标标志器上的光点存在常值安装偏差时，采用双目测量算法求解，其最大解算误差固定，不随纵向距离的变化发生改变.

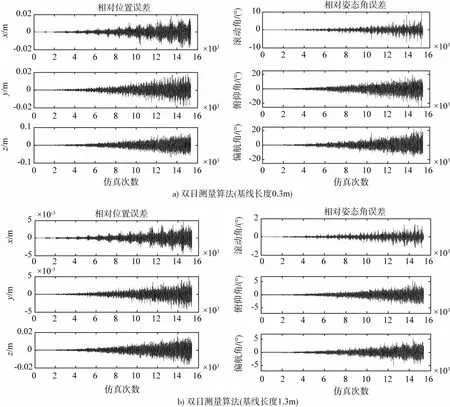
图5 像点提取存在1μm随机误差情况下的测量算法解算误差仿真曲线

3 结论

本文针对适用于空间交会对接过程中CCD光学成像敏感器的双目测量算法展开研究，推导了基于主像机坐标系的双目测量算法计算公式，并重点对其抗干扰能力进行研究，该算法的优点是建立在单个像机坐标系上，可方便的与单目算法进行切换，其抗干扰能力主要取决于误差源大小、像机焦距、基线长度，最后对该双目测量算法进行了仿真分析，仿真结果表明该算法计算精度可以满足要求，但当存在像点提取误差时，姿态解算精度受影响较大，增大基线长度可以有效降低该解算误差.

[1] 吴宏鑫，胡海霞，解永春，等.自主交会对接若干问题[J].宇航学报，2003，24(2):132-137

[2] 解永春，张昊，石磊，等.交会对接光学成像敏感器设计中的关键问题[J].航天控制，2006，24(5):35-39

[3] Gao X S，Hou X R.Complete solution classification for the perspective-three-point problem[J].IEEE Trans.on Pattern Analysis and Machine Intelligence， 2003， 25(8):930-943

[4] Calhoun P.A solution to the problem of determining the relative 6 DoF state for spacecraft automated rendezvous and docking[J].SPIE，1995，2466:176-184

[5] 曹喜滨，张世杰.航天器交会对接位姿视觉测量迭代算法[J].哈尔滨工业大学学报，2005，37(8):1123-1126

[6] 唐宁.交会对接测量系统研究[D].北京:北京控制工程研究所，2002

[7] 李庆扬，莫孜中.非线性方程组的数值解法[M].北京:科学出版社，1999

[8] 刘钦圣.最小二乘问题计算方法[M].北京:北京工业大学出版社，1989

A CCD Optical Sensor Based New Binocular Vision M easurem ent A lgorithm for Rendezvous and Docking

ZHANG Hao1，2， SHI Lei1，2， TU Junfeng1，2， GUAN Yuexin1，2， XIE Yongchun1，2
(1.Beijing Institute of Control Engineering， Beijing 100190， China;2.Science and Technology on Space Intelligent Laboratory， Beijing 100190，China)

In the final approach phase of space rendezvous and docking(RVD)，as a primary measurement sensor，the CCD optical sensor can provide the information of relative navigation.The accuracy of its real-time measurement is the determ inants on the success of RVD.A new binocular algorithm based on main CCD camera as the vision algorithm of CCD optical sensor for rendezvous and docking is studied in this paper.The noise resistance ability of the binocularmeasurement algorithm is studied by using theoretical analysis and results of numerical simulation are provided.

rendezvous and docking;CCD optical sensor;binocular measurement algorithm;noise resistance