粒子滤波及其在航天器交会对接相对导航中的应用

2011-11-25解永春胡海霞

空间控制技术与应用 2011年6期

关键词：概率密度后验权值

刘涛，解永春，胡海霞

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

粒子滤波及其在航天器交会对接相对导航中的应用

刘涛1，2，解永春1，2，胡海霞1，2

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

在全面分析粒子滤波原理的基础上，提出一种改进高斯粒子滤波方法.该方法利用确定性采样滤波算法进行时间更新，替代高斯粒子滤波算法中的随机采样过程;另外，针对厚尾噪声情况，利用鲁棒统计方法对确定性采样滤波方法进行鲁棒性改进，并将其应用于所提出的改进高斯粒子滤波.将粒子滤波算法应用于交会对接相对导航问题，仿真结果表明，在多种测量噪声情况下，改进高斯粒子滤波较其他粒子滤波，能够在不过多损失估计精度的同时有效降低计算量.文中的研究成果为将粒子滤波应用于航天器导航问题提供了理论参考.

粒子滤波;高斯粒子滤波;确定性采样滤波;交会对接 ;相对导航

统计滤波方法在导航、信号处理以及金融等领域均有着广泛应用.离散随机系统可描述如下:

其中，Xk∈Rn为系统状态，Z∈Rm为测量量，f(·)和h(·)分别为过程方程和测量方程，w和v分别表示过程噪声和测量噪声.对于如式(1)和(2)所示的系统，从贝叶斯估计的观点看，状态的后验概率密度包含了有关状态的所有可用信息，已知后验概率密度可根据不同的最优估计指标，得到相应的最优估计结果[1].但是，递推形式的贝叶斯估计需要求解高维积分，只有在线性高斯以及离散有限状态等几种特殊情况下才能得到精确解析解，而对于一般系统，后验概率密度本质上需要无穷参数进行描述，所以只能对贝叶斯估计算法进行近似.

20世纪50年代有学者将蒙特卡洛(MC，Monte Carlo)数值积分方法引入到贝叶斯估计理论，形成了基于序列重要性采样方法(SIS，sequential importance samp ling)的近似贝叶斯估计方法.20世纪90年代开始，标志性成果是英国学者Gordon等所提出的Bootstrap Particle Filtering:BPF方法[2].

粒子滤波在实际应用中的主要障碍是其庞大的计算量.为此，有学者提出一种不需要重采样的类粒子滤波—高斯粒子滤波(GPF，gaussian particle filtering)[3].高斯粒子滤波设定后验概率密度p(Xk+Z1:k+1)服从高斯分布，所以不需要进行重采样.高斯粒子滤波仍然属于高斯滤波的范畴，但是不再基于线性最小方差估计框架，而是借助重要性采样(IS，importance sampling)对后验概率密度进行近似，可以方便的求取各阶矩，而且对任意分布的噪声均适用.

航天器轨道确定问题本质上是非线性/非高斯的状态估计问题，非线性较强的测量方程和非高斯的测量噪声是滤波器设计中需要重点克服的难点.现有的航天器轨道确定问题主要采用EKF、UKF[4]、DDF[5]和GHF[6]等基于线性最小方差估计框架的滤波算法行进设计，这些方法虽然在很多情况下可以得到比较精确的滤波估计结果，但受制于这些方法的结构性缺陷，使得其在针对非线性比较强，噪声呈现明显非高斯分布的系统时很难提供高精度的估计结果，将粒子滤波应用于航天器导航问题中显然具有意义，但是，星载计算机的计算能力有限，现有的各种粒子滤波都会带来沉重的计算负担，这成为将粒子滤波应用于航天器导航问题的主要障碍.

本文针对航天器导航的特点，对现有的高斯粒子滤波进行改进得到一种新的计算量更小的改进高斯粒子滤波.

1 贝叶斯估计

对于如式(1)和(2)所示的系统，设定状态序列为马尔可夫随机序列，则贝叶斯估计可按照以下形

式递推得到状态的后验概率密度:以上推导中利用的是状态的时间序列 X0:k+1，

许多文献中仅仅考虑对k+1时刻的状态进行估计，

这相当于对式(3)求取边缘分布

其中，

虽然边缘分布便于理解滤波问题，但是基于状态序列的形式便于更好的理解SIS的本质.

贝叶斯估计中必须进行如式(4)和(6)所示的高维积分，对一般系统很难得到精确的解析解，只能进行近似.

2 粒子滤波

将MC数值积分方法引入贝叶斯估计框架可以得到近似的贝叶斯估计，由此形成了粒子滤波.下面对粒子滤波的原理进行介绍.

2.1 蒙特卡洛数值积分

对于任意函数的期望可近似为:

可以证明，MC数值积分的估计误差量级为ο(1/N)，估计精度与状态的维数无关.

MC数值积分方法主要存在两个难点[1]:

(1)p( X0:Z0:k)未知或形式特殊时，很难直接从p( X0:Z0:k)进行采样;

(2)计算量随时间增长.

2.2 重要性采样(IS，im portance sam p ling)

为了解决MC数值积分方法中的第一个难点，IS方法被引入到MC数值积分问题中.IS方法引入了重要性密度(proposal distribution)q(X0Z1:k)，而q(X0:Z1:k)必须与 p(X0Z1:k)相似，即满足

p(X0:k|Z1:k)＞0⇒q(X0:k|Z1:k)＞0 (9)并且，所选择的q(X0:k|Z1:k)应该容易从其中进行采样.采用IS方法后MC数值积分可以写作以下形式[7]:

其中

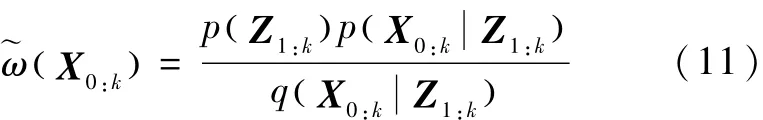
表示归一化之前的权值.

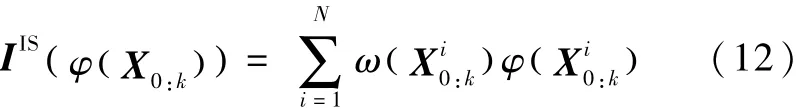
IS方法的优势在于[1]:

(1)可以克服p(X0:k|Z1:k)不好采样的问题;

(2)提供了一条途径，以减小估计协方差;

(3)重要性密度的支集通常较后验概率大，这样对测量野值(Outlier)具有鲁棒性.

IS方法的不足在于存在退化问题，即尽管理论上估计偏差随着N的增大逐渐减小，但实际上，计算中会出现仅仅有部分粒子的权值比较大，而大部分权值都很小的情况，使得计算量浪费在对估计贡献很小的小权值粒子上，而能够表征后验概率密度主要部分的粒子却很少，从而大大降低了估计效果.

2.3 序列重要性采样(SIS)

为了克服MC数值积分方法中的第2个问题，可对IS方法进行序列化改进.为此，在选择重要性密度函数时使其满足:

其中，ω表示归一化之后的权值.

式(12)的计算过程相当于对后验概率密度进行了如下离散近似:从而使得k+1时刻仅仅需要根据qk+1采样获得，而无需从新对整个状态序列进行采样.完成采样后，相应的权值通过递推得到:

由此可见，采用SIS方法使得计算量与时间增长无关.SIS的缺点在于:SIS仅仅是IS的一种特殊情况，所以和IS一样存在着粒子退化的问题.

2.4 重要性密度的选择

克服SIS方法粒子退化的有效方法之一就是选择适合的重要性密度.通常重要性密度的选择应该遵循以下几点:

(1)其支集应该不小于p(X0:k+Z1:k+1)的支集;(2)应该满足递推计算的要求;

(3)应该使得权值的方差最小化.

可以证明，使得权值方差最小的最优重要性分布为但是，最优重要性密度通常很难获得.因此，对最优重要性密度的近似是粒子滤波一个重要的研究方向.

2.5 重采样

克服粒子退化的另一重要方法就是粒子重采样.重采样的基本思想是抑制或剔除小权值粒子，对于大权值粒子则依其权值大小进行复制，从而把处理资源按照粒子权值的大小进行分配.重采样的方法主要有[8]:多项式重采样(multinom ial resamp ling)、剩余重采样(residual resamp ling)、最小方差采样(m inimum variance samp ling)或系统重采样(systematic resamp ling).一般计算中系统重采样方法应用最为广泛.重采样在克服粒子退化的同时会带来粒子多样性降低的贫化问题，克服重采样后的粒子贫化问题也是粒子滤波改进的重要研究方向.

2.6 粒子滤波算法

将SIS方法引入贝叶斯估计，就构成了粒子滤波算法.

则得到粒子滤波中所采用的权值递推公式

对权值归一化后，后验概率密度可近似为

粒子滤波的主要优势在于:1)对非线性/非高斯系统均适用;2)直接对后验概率密度进行近似，理论上可以获得任意精度的估计结果.

目前，有关粒子滤波性能的研究和改进主要集中在3个方面:1)重要性密度的选择;2)克服粒子退化以及重采样后的粒子贫化.典型的方法如RPF(Regularized Particle filer)以及基于MCMC移动方法的粒子滤波[10];3)减小计算量.为解决粒子数目的适当选择，有学者提出自适应粒子滤波[11]，另一条思路就是第3节将要介绍的高斯粒子滤波方法.

3 高斯粒子滤波

为了避免进行重采样，文献[3]提出了一种类粒子滤波方法—高斯粒子滤波方法.该方法设定状态预测概率密度和后验概率密度均服从高斯分布，从而不需要进行粒子递推，进而避免粒子退化问题，也就不需要进行重采样.高斯粒子滤波具体算法简述如下:

从表2的统计结果可以看出,除环境/生态科学和地球科学这个研究领域外,在其他领域,高被引论文作者认为存在5个以上竞争者的比例均高于普通论文作者,这说明整体而言,高被引论文作者所面临的竞争环境比普通论文作者更加严峻。但是,学者们进行科学研究所面临竞争环境的激烈程度是有上限的。调查结果显示,仅有3%的高被引论文作者认为存在超过10个竞争者,仅有5%的普通论文作者认为存在超过10个竞争者。除计算机科学和数学、环境/生态科学和地球科学以外,在其他学科中,非常关心优先发表权的高被引论文作者比例远远超过普通论文作者。

第二部分:测量更新

(3)后验概率密度可以写为

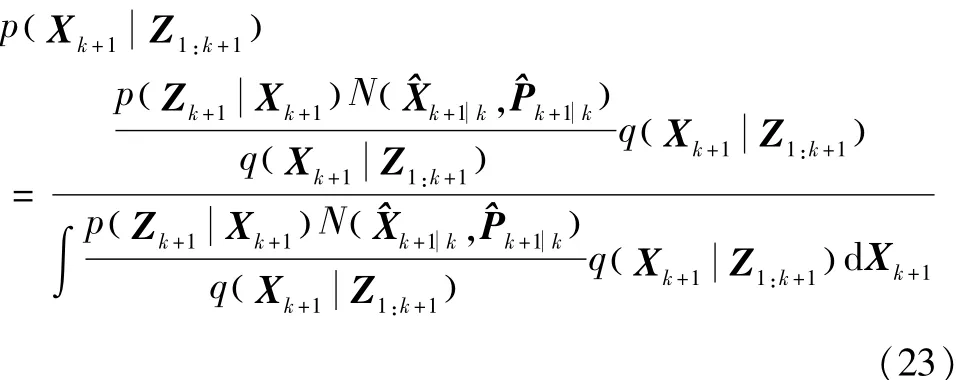
将权值归一化，可以得到后验概率密度的近似形式为

利用后验概率密度的近似形式求取均值 ^Xk+1和协方差，设定后验概率密度服从高斯分布:

几点说明:1)高斯粒子滤波时间更新部分需要设定预测概率密度满足高斯分布，其目的有两个:首先，由式(24)的形式可知，权值的求取必须已知预测概率密度的形式;另外，设定预测密度为高斯分布从理论上可以保证测量更新步骤给出的预测概率密度趋近于高斯分布;2)采用重要性密度的原因是替代后验概率密度，所以重要性密度应与后验概率密度尽量相似.实际应用中为方便起见，常直接将预测概率密度近似分布 N Xk+1|^Xk+1|k，^Pk+1|(

)k作为重要性密度，由此会带来与BPF相似的问题，即由于未引入最新的测量信息而加剧粒子的退化.

4 改进的高斯粒子滤波

改进思路简述如下:高斯粒子滤波采用随机采样方式得到预测概率密度的高斯近似，理论上可以得到更加精确的一阶矩和二阶中心距的估计，但计算量很大.在状态方程非线性不强，过程噪声比较小且服从高斯分布的情况下，时间更新部分采用确定性采样滤波方法，所得到的估计结果应该可以满足要求，这样可以节省大量的计算量;另外，为优化重要性密度，可利用确定性采样滤波方法测量更新后的估计结果作为重要性密度加以应用.

由于航天器轨道确定问题中经常采用光学敏感器作为测量手段，而光学敏感器尤其是雷达，其测量噪声多呈现厚尾分布[12]，厚尾分布带来的突出问题就是测量野值(outlier)的频繁出现，而基于线性最小方差估计框架的滤波器对测量野值很敏感[13].文献[14]利用Huber鲁棒统计算法对DDF进行鲁棒性改进，Huber鲁棒统计通过结合l1和l2范数估计器的特点，使其估计性能在测量误差含有粗差的情况下具有较好的适应性，从而使改进后的DDF对厚尾分布具备鲁棒性.本文借鉴文献[14-15]的思想，对UKF方法进行改进，并将其应用于改进高斯粒子滤波.

现将所提出的改进高斯粒子滤波阐述如下:

第一部分:利用确定性采样滤波方法完成时间更新，生成预测概率密度:

(1)k=0，进行滤波初始化

(2)产生采样点

采用 Scaled UT采样方式生成采样点 χi，k和相应权值和

(3)生成预测概率密度

预测概率密度设定为

第二部分:引入鲁棒统计方法对 UKF进行改进，以生成重要性密度

(4)重新采样

(5)预测观测值

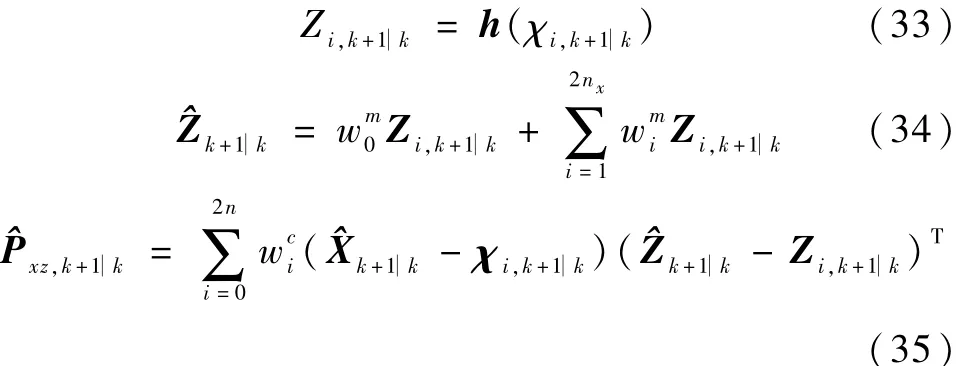
(6)生成重要性密度

对测量进行线性化近似

其中，

构造以下变量:

设

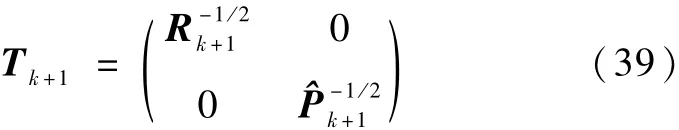
利用Tk+1左乘式(38)两端，记做

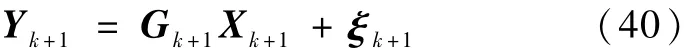
滤波器设计取决于下式的求解:

其中，

(·)i表示向量的第 i个元素，γ为可调节参数，一般取为γ=1.345[15].

由式(41)容易得到:

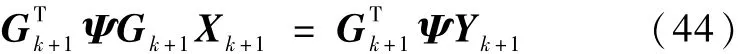
其中，Ψ为对角线矩阵，其对角线元素由式(43)所示的各元素构成.由于Ψ与Yk+1有关，所以需要利用迭代的方法求取式(44)，具体求解过程为

其中，初始值由下式确定

估计误差协方差阵为

其中，Ψ为迭代步骤最后一步的取值.迭代的步数可人为设定.

设定重要性密度为

将以上改进后的 UKF称为鲁棒 UKF，记做RUKF.

第三部分:利用IS方法进行测量更新

(8)得到相应的权值

(9)权值归一化后，进行状态估计

需要指出的是，重要性密度可以直接取为 N作为重要性密度更适合.

5 数学仿真

本节将所提出的改进高斯粒子方法，应用于设计基于激光雷达的航天器交会对接相对导航滤波器.

建立如下相对导航坐标系:原点为目标航天器的质心，z轴指向地球的质心，y轴垂直于 z轴，指向轨道角速度方向，x轴与z、y轴构成右手系.在设定的导航坐标些中，以相对位置和速度为状态的相对导航系统模型为[16]

激光雷达可提供相对距离ρ和相对视线仰角α以及视线方位角β，测量方程为:

式(56)中Cmr为相对导航坐标系到激光雷达测量坐标系的方向余弦阵.

设定目标航天器位于轨道高度为400km的近圆地球轨道.

初始相对状态为

从理论上分析，GHF方法可以得到比 EKF、UKF和DDF更精确的估计结果，为了通过比较说明本文所提出方法的有效性，仿真中采用GHF作为基于线性最小方差估计框架方法的代表，而RGHF表示鲁棒GHF算法，其设计思路与RUKF一样.

共利用GHF、RGHF、BPF以及4种高斯粒子滤波算法设计7个滤波器.4种高斯粒子滤波中，GPF1表示预测概率密度为重要性密度的高斯粒子滤波器;GPF2表示采用RUKF生成重要性密度的高斯粒子滤波器;MGPF1表示预测概率密度作为重要性密度的改进高斯粒子滤波器;MGPF2表示利用RUKF生成重要性密度的改进高斯粒子滤波器.

仿真中，粒子数取为2000，GHF的一维采样数设为3.以均方估计误差为估计精度的衡量标准，即滤波器初始值设定为:

以下分析中位置单位均为 m，速度单位均为m/s.

仿真1.考察测量噪声服从高斯分布时，各滤波器的性能，其中测量噪声满足:

由图1～4和表1可以看到，当测量噪声服从高斯分布时，7种方法的估计精度非常接近.理论上讲，粒子滤波较基于线性最小方差估计算法的优势在于可以克服非线性和非高斯测量噪声的影响，但交会对接相对导航问题中测量方程的非线性性不算很强，而测量噪声为高斯分布时，各种粒子滤波较基于线性最小方差估计的方法优势并不明显.

仿真2.考察测量噪声服从厚尾分布时，各滤波器的性能，测量噪声满足:

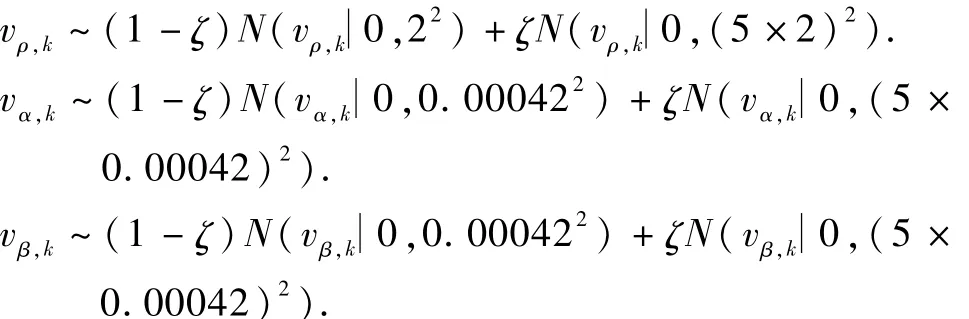
其中，ζ=0.3.

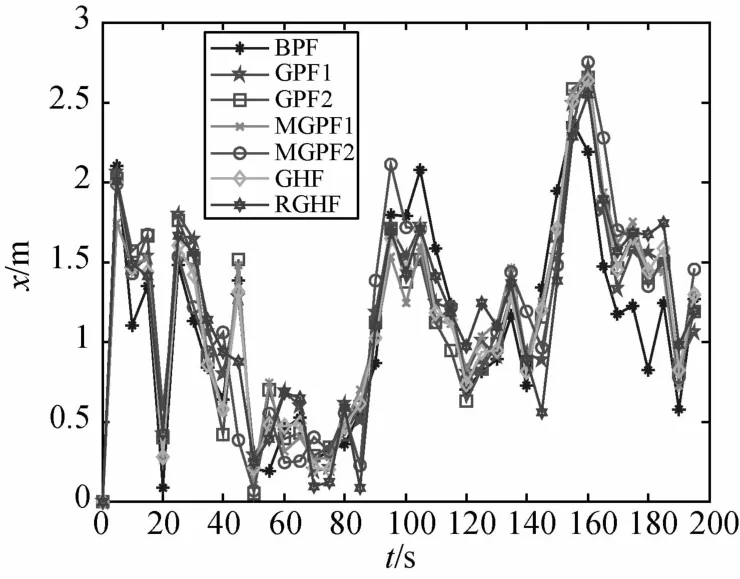
图1 高斯测量噪声时x轴相对位置估计误差

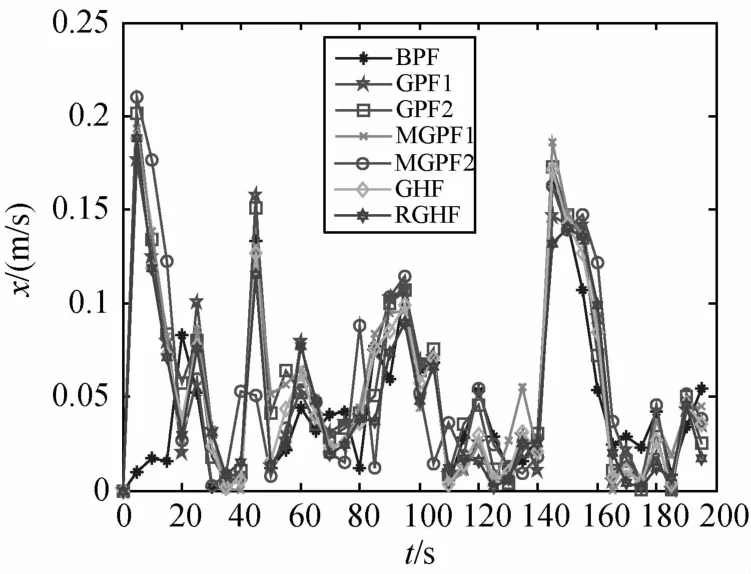
图2 高斯测量噪声时x轴相对速度估计误差

图3 高斯测量噪声时z轴相对位置估计误差

图4 高斯测量噪声时z轴相对速度估计误差

表1高斯测量噪声时各滤波器的均方估计误差

图5 厚尾测量噪声时x轴相对位置估计误差

图6 厚尾测量噪声时x轴相对速度估计误差

图7 厚尾测量噪声时z轴相对位置估计误差

图8 厚尾测量噪声时z轴相对速度估计误差

表2厚尾测量噪声时各滤波器的均方估计误差

表3 各滤波器的运行时间

厚尾分布是光学敏感器常见的测量噪声分布.可以看到GHF滤波器得到的估计结果精度很差，而采用RGHF方法可以显著提高估计精度，这证实了将鲁棒统计的思想引入基于线性最小方差估计框架的滤波算法能够克服厚尾分布测量噪声的不利影响.5种粒子滤波较RGHF方法的估计精度还要略高一些，这也说明当测量噪声服从非高斯分布时，粒子滤波具有优势.5种粒子滤波中，4种高斯粒子滤波器较BPF精确，而两种改进高斯粒子滤波与一般高斯粒子滤波的估计精度很接近，但从运行时间来看，MGPF1较GPF1，MGPF2较GPF2的运行时间均有明显下降，也证实了所提出改进高斯粒子滤波方法在不过多损失估计精度的同时可以有效降低计算量.

仿真3.考察测量噪声服从gamma分布时，比较各滤波器的性能，设定测量噪声满足:

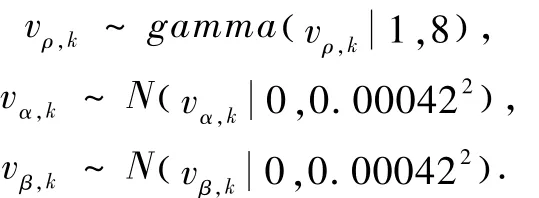
表4 gamm a 测量噪声时各滤波器的均方估计误差

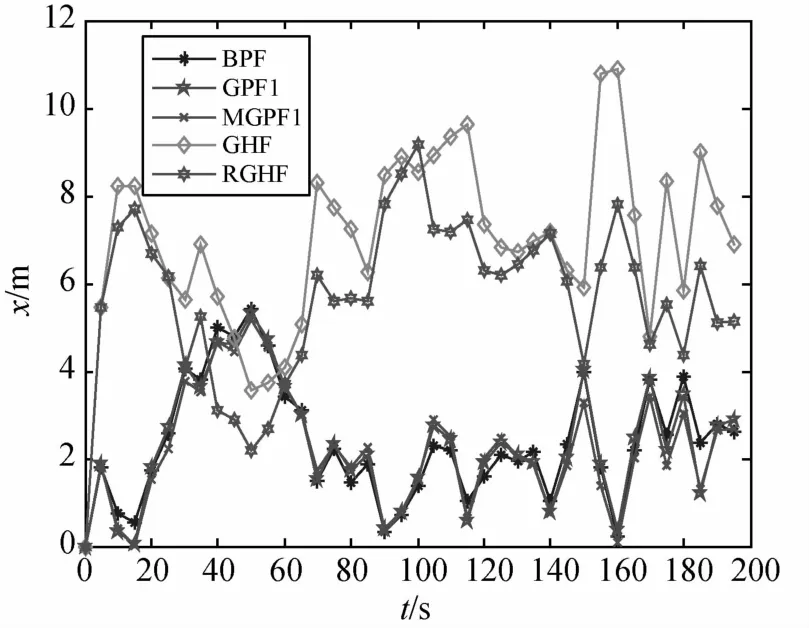
图9 gamma测量噪声时x轴相对位置估计误差

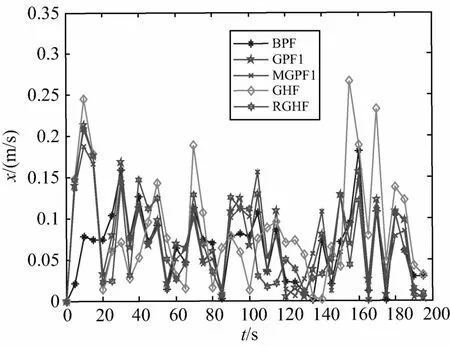
图10 gamma测量噪声时x轴相对速度估计误差

与厚尾分布不同，gamma分布是一种典型的非对称分布，在该情况下不便采用UKF方法生成重要性密度.从仿真结果可以看到，对厚尾测量噪声有效的RGHF效果很差，而3种粒子滤波方法可以得到比较精确的估计结果，而且MGPF1较BPF的估计精度要高，较 GPF1略低.本算例仿真说明，粒子滤波可在各种非高斯测量噪声情况下提供高精度的滤波估计结果，这是基于线性最小方差框架滤波器所不具备的，而本文所提出的改进高斯粒子滤波以较小的计算量获得了精度较高的估计结果，也说明了其有效性.

图11 gamma测量噪声时z轴相对位置估计误差

图12 gamma测量噪声时z轴相对速度估计误差

6 结束语

粒子滤波为处理非线性/非高斯系统的滤波估计问题提供一条有效途径，但其庞大的计算量使得将其应用于航天器自主导航等实际问题存在困难.为此，本文在全面分析粒子滤波原理的基础上，对现有的高斯粒子滤波进行适应性改进得到一种改进高斯粒子滤波.将所提出的方法应用于交会对接相对导航问题，仿真结果证实所提出的改进高斯粒子滤波方法，能够在多种测量噪声情况下，提供高精度的估计结果，且其计算量较一般高斯粒子滤波要小.

[1] Chen Z.Bayesian filtering:from kalman filters to particle filters，and beyond[R].McMaster University， 2003

[2] Gordon N，Salmond D，Smith A FM.Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J].IEEE， 1993，140(2):107-113

[3] Kotecha J H，Djuric P A.Gaussian particle Filtering[J].IEEE Trans Signal Process，2003 51(10):2592-2601

[4] Julier S，Uklmann J.Unscented filtering and nonlinear estimation[J].IEEE，2004，92(3):401-422

[5] Magnus N，Niels K.P.New developmentsin state estimation for nonlinear systems[J].Automatica，2000，36:1627-1638.

[6] Ienkaran A，Simon H.Discrete time nonlinear filtering algorithms using Gauss-Hermite quadrature[J].IEEE，2007，95(5):953-977

[7] Arnaud D，Simon G，Christophe A.On sequentialmonte carlo sampling methods for bayesian filtering[R].University of Cambridge，2000

[8] 程水英，张剑云.粒子滤波评述[J].宇航学报，2008，29(4):1099-1111

[9] Cheng S Y，Zhang J Y.Review on Particle Filters[J].Journal of Astroautics，2008，29(4):1099-1111

[10] Rudolph V D M.Sigma-point Kalman filters for probabilistic inference in dynamic state-spacemodels[D].PH.D dissertation of Oregon Health and Science University，2004

[11] Branko R.Beyond the Kalman fitler:particle filters for tracking applications[M].Boston:Artech House，2004

[12] Fox D.Adapting the sample size in particle filters through KLD-sampling[J].IEEE Trans.Robotics，2003 22(12):985-1003

[13] Christopher D K.Robust rendezvous navigation in elliptical orbit[J].Journal of Guidance， Control， and Dynamics， 2006， 29(2):495-499

[14] Huber P J.Robust Statistics[M].New York:W iley，1981

[15] Christopher D K.Huber-based divided difference filtering[J].Journal of Guidance， Control， and Dynamics，2007，30(3):885-890

[16] Karlgaard C D，Schaub H.Comparison of several nonlinear filters for a benchmark tracking problem[C].AIAA 2006-6243，2006

[17] Wigbert F.Automated rendezvous and docking of spacecraft[M].London:Cambridge University Press，2003

App lication of Particle Filtering in Relative Navigation Filter Design for Spacecraft

LIU Tao1，2，XIE Yongchun1，2，HU Haixia1，2
(1.Beijing Institute of Control Engineering， Beijing 100190， China;2.Science and Technology on Space Intelligent Control Laboratory， Beijing 100190， China)

Based on analyzing the theory of Particle filtering，a novelmodified Gaussian Particle Filtering is proposed in this paper.In the new filter，a determ inistic samp ling filtering is used to fulfil the time update instead of random samplingmode;Furthermore，deterministic sampling filtering ismodified by using a robust statisticalmethod tomake it robust for heavy-tail noise，and the result of the robust determ inistic sampling filtering is adopted as the proposal distribution.Themodified Gaussian particle filter is used in the relative navigation filter design for RVD，and the simulation results show the efficiency of the new method.The results in this paper are the valuable reference for practical application of particle filtering in space navigation field.

particle filtering;gaussian particle filter;deterministic sampling filtering;rendezvous and docking relative navigation