大跨径钢管混凝土拱桥自振特性分析与动载试验
2011-11-24汤建林宋景景
汤建林,宋景景
(浙江省交通运输厅工程质量监督局检测中心,杭州311215)
桥梁结构的自振特性主要包括结构的自振频率、振型、阻尼比等。拱桥的自振特性主要取决于桥跨结构的组成体系、各构件的刚度、质量分布及支承条件等因素。拱桥的自振特性分析对合理地进行桥跨结构的抗震设计、抗风稳定性分析及车振分析等都有着重要的意义[1]。本文通过横塘港大桥自振特性分析及动载试验结果,对该桥结构的使用性能和整体刚度进行分析评估。
1 工程概况
横塘港大桥位于浙江省桐乡市,跨越横塘港,桥梁全长1 040 m。主桥为跨径144 m的钢管混凝土拱桥,引桥为25 m和30 m装配式部分预应力混凝土连续箱梁。桥面净宽2×净-11.75m,设计荷载为公路-I级,按双向4车道设计。主桥上部结构采用144 m下承式钢管混凝土系杆拱,计算跨径为140 m,拱轴线形为二次抛物线,矢跨比为1/5,拱肋断面形式为横哑铃型,横向设置三片拱肋,一片中拱肋和两片边拱肋。下部结构采用柱式桥墩、钻孔灌注桩基础。拱桥上部结构采用C50混凝土,桥墩墩身采用C30混凝土,基桩采用C25水下混凝土。
2 动力分析模型
为了与动载试验结果进行比较,并对桥梁自振特性进行评估,采用桥梁空间分析程序MIDAS对该桥主桥建立有限元空间模型。主桥空间分析计算模型如图1所示。

图1 主桥空间分析计算模型图
3 桥梁自振特性理论分析
3.1 基本方程
在无外力作用时,同时不考虑阻尼作用,结构动力分析的无阻尼方程为:
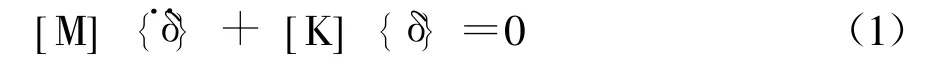
(1)式中:[M]为质量矩阵;[K]为整体刚度矩阵;{δ}为整个结构的节点位移列阵;{¨δ}为对 {δ}求二次导。
该方程为二阶常系数线性奇次常微分方程组,式 (1)的解为:

(2)式中:{A}为组合截面面积列阵;ωi(i=1,2,...,n)为结构的固有频率;φ为结构的相位角。
系统的特征值列式为:

3.2 自振特性理论计算
在拱桥动力特性分析中,一般情况下结构的前几阶自振频率和振型起控制作用,所以本文只求解该桥的前五阶自振频率和振型。用MIDAS建立的有限元空间模型计算了该桥的前五阶自振频率及对应振型图。前五阶自振频率及振型特征见表1,振型图如图2~图6所示。
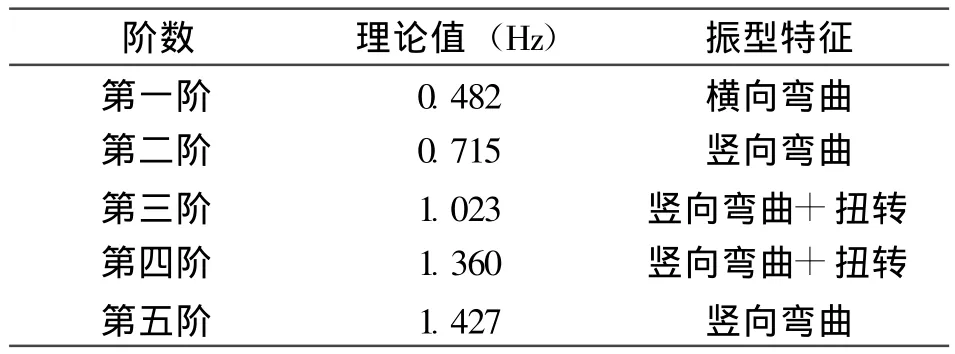
表1 横塘港大桥前五阶理论计算自振频率表

图2 一阶振型图(f1=0.482Hz)

图3 二阶振型图(f2=0.715Hz)
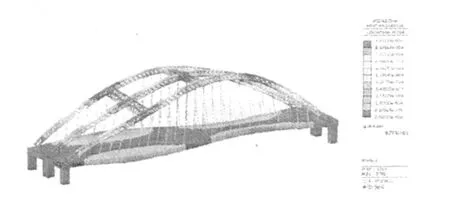
图4 三阶振型图(f3=1.023Hz)

图5 四阶振型图(f4=1.360Hz)
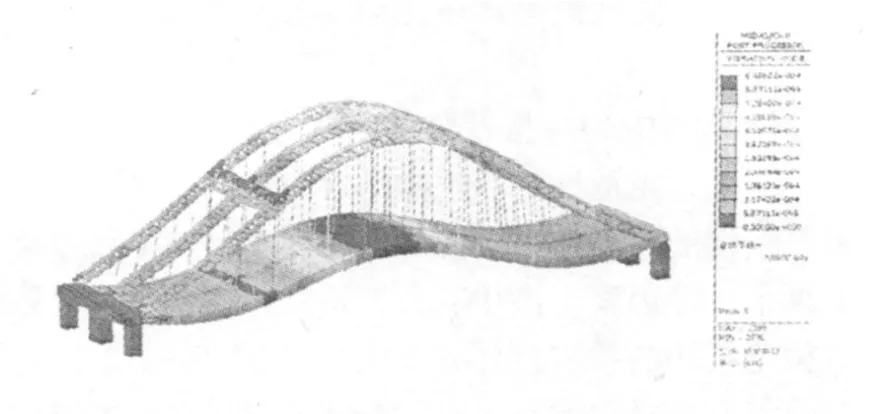
图6 五阶振型图(f5=1.427Hz)
4 动载试验测试
4.1 试验方法和仪器
拱桥的自振特性主要取决于桥跨结构的组成体系、各构件的刚度、质量分布及支承条件等因素,而与外荷载等其他条件无关。桥梁自振特性的测量一般分为瞬态激振法、强迫振动法和脉动法。该桥自振特性测量选用脉动法。用脉动法测量桥梁的自振特性,具有不需要对桥梁进行专门激励的优点,只要有高灵敏度的测量仪器和高分辨率的谱分析设备就能准确地测出结构的自振特性。该桥自振特性测试中振动位移的测量传感器采用DPS型低频位移传感器,后续的调理器及数据采集设备分别采用VA-99低通滤波放大器以及南京安正软件公司的AZ-108数据采集箱和振动及动态信号采集、分析系统,最后通过带模态分析软件的计算机进行分析。
该桥自振特性测量时在主桥顺桥向八分点处布设位移传感器,每个断面横桥向布置如图7所示。选择八分之三点处作为参考测点的位置,将测振传感器布置在参考测点及其他测点处,测量各测点的时域振动信号,然后参考测点处的传感器不动,将其他测点处的传感器依次移动到尚未进行过测量的测点处,再测量各测点处的时域振动信号,直至对所有的测点都进行测量。

图7 自振特性测点横桥向布置示意图
4.2 自振特性实测值
通过对采集到的动态信号进行模态分析,得到该桥的前五阶自振频率及相应的阻尼比。自振特性实测值与理论值对比见表2,实测振型图如图8~图12所示。
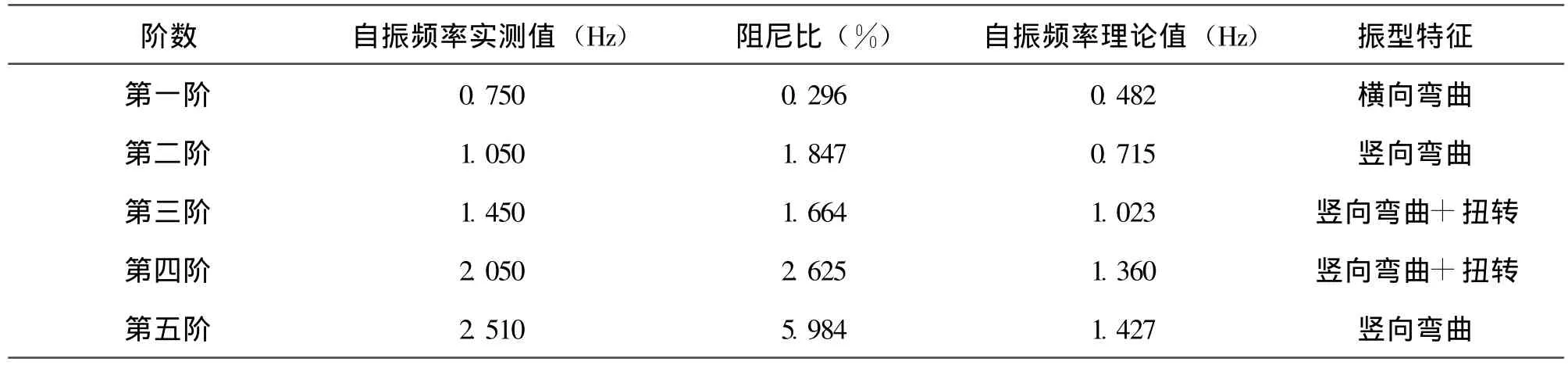
表2 横塘港大桥自振特性实测值与理论值对比表
图8 一阶实测振型图 (f1=0.750Hz)
图9 二阶实测振型图 (f2=1.050Hz)

图10 三阶实测振型图 (f3=1.450Hz)
图11 四阶实测振型图(f4=2.050Hz)

图12 五阶实测振型图(f5=2.510Hz)
5 结 语
(1)桥梁结构前五阶自振频率实测值均较理论分析计算值稍大,说明桥梁结构整体性好,动刚度较大。
(2)实测结构阻尼比在 0.296%~5.984%之间,在一般桥梁阻尼比1%~10%的合理范围内。
[1]肖志海.中承式劲性骨架拱桥动力特性分析[D].武汉:武汉理工大学,2009.
[2]宋一凡.公路桥梁荷载试验与结构评定[M].北京:人民交通出版社,2002.
[3]交通部公路科学研究所,等.大跨径混凝土桥梁的试验方法[K].北京:交通部公路科学研究所,1982.
