黄铁矿、白铁矿和磁黄铁矿的电子结构及可浮性
2011-11-24陈建华钟建莲李玉琼
陈建华, 钟建莲, 李玉琼, 陈 晔, 郭 进
(1. 广西大学 资源与冶金学院, 南宁530004;2. 广西大学 化学化工学院,南宁530004;3. 广西大学 物理科学与工程技术学院, 南宁530004)
黄铁矿、白铁矿和磁黄铁矿的电子结构及可浮性
陈建华1, 钟建莲1, 李玉琼2, 陈 晔1, 郭 进3
(1. 广西大学 资源与冶金学院, 南宁530004;2. 广西大学 化学化工学院,南宁530004;3. 广西大学 物理科学与工程技术学院, 南宁530004)
采用基于密度泛函理论的第一性原理方法,计算黄铁矿、白铁矿和磁黄铁矿的电子结构,讨论这 3种硫铁矿的电子结构与其可浮性之间的关系。计算结果表明:黄铁矿为直接带隙半导体,白铁矿为间接带隙半导体,而磁黄铁矿为导体。态密度分析结果表明,黄铁矿和白铁矿为低自旋态,而磁黄铁矿则为自旋−极化态。前线轨道计算表明:这3种硫铁矿被氧化由易到难的顺序为磁黄铁矿,白铁矿,黄铁矿;用黄药捕收的可浮性由强到弱的顺序为白铁矿,黄铁矿,磁黄铁矿。计算结果能够很好地解释这3种硫铁矿与氧气作用的难易程度以及用黄药捕收的可浮性顺序。
黄铁矿;白铁矿;磁黄铁矿;电子结构;可浮性;密度泛函理论
自然界中常见的硫铁矿有3种:黄铁矿、白铁矿和磁黄铁矿,它们经常与其他有用金属硫化矿物(如铜、铅和锌硫化矿)共同存在,也经常存在于煤中,因此,在浮选实践中经常需要将硫铁矿与其他矿物分离。虽然这些矿物都由铁原子和硫原子组成,但其晶体结构和性质大不相同,从而导致它们在浮选过程中表现出不同的浮选行为。在硫化矿浮选实践中发现,白铁矿的可浮性与黄铁矿的相似,但比磁黄铁矿的好,这3种硫铁矿用黄药捕收的可浮性由强到弱的顺序为白铁矿,黄铁矿,磁黄铁矿[1]。另外,这 3种硫铁矿被氧化的难易程度也存在差异,其中,磁黄铁矿最容易被氧化,其次为白铁矿,黄铁矿远不如前两种[2]。已有的研究结果表明,黄药在黄铁矿、白铁矿和磁黄铁矿上的反应过程是一个电化学过程,其产物均为双黄药[3],矿物的电化学性质取决于矿物的半导体性质和电子结构[4]。因此, 研究硫铁矿的电子结构对于揭示不同硫铁矿可浮性的差异具有重要的意义。
基于密度泛函理论的第一性原理是计算电子结构的有效方法。目前,国内外学者采用第一性原理对闪锌矿[5−7]、黄铜矿[8]、方铅矿[9]和黄铁矿[10]的电子结构进行了计算,获得了比较准确的计算结果。硫铁矿实际矿物的浮选试验研究已有不少报道,但未见关于硫铁矿的电子结构与其可浮性关系研究的报道。为了解硫铁矿的电子结构与其可浮性之间的关系,本文作者采用密度泛函理论的第一性原理研究黄铁矿、白铁矿和磁黄铁矿的电子结构,采用前线轨道理论讨论这3种硫铁矿与氧气的作用机理及用黄药捕收的可浮性顺序。

表1 3种硫铁矿不同交换关联函数的优化结果Table 1 Optimized results of different exchange correlation functions of three sulfurous iron minerals
1 计算方法及模型
1.1 计算方法
采用软件Material Studio 4.2中的CASTEP模块,基于密度泛函的第一性原理方法[11]对黄铁矿、白铁矿和磁黄铁矿 3种硫铁矿的能带结构、电子态密度和Mulliken布居进行计算。首先,对此3种硫铁矿的原胞模型进行优化处理,以选取较佳的交换关联函数和平面波截断能,不同交换关联函数和截断能的计算结果分别如表1和2所列。
由表 1可知,对于黄铁矿,用函数 GGA-PW91计算出的晶格常数与实验值a=b=c=0.541 7 nm[12]非常接近; 对于白铁矿,用函数GGA-PW91和GGA-PBE计算出的晶格常数都分别与实验值 a=0.444 5 nm,b=0.542 5 nm,c=0.338 6 nm[14]比较接近;对于磁黄铁矿,用函数 GGA-RPBE计算出的晶格常数与实验值a=b=0.686 5 nm,c=1.704 6 nm[16]较接近。综合考虑晶格常数和带隙宽度与实验值的误差以及能量的大小,黄铁矿和白铁矿的交换关联函数采用GGA-PW91,磁黄铁矿的交换关联函数采用GGA-RPBE。平面波截断能测试结果见表2。由表2可知,截断能取270 eV较为合理。另外,采用超软赝势[17−18]来描述离子实和价电子间的相互作用,对电荷密度和体系总能量在Brillouin区的积分计算采用 Monkhorst-Pack (MP)方案[19]。在选择交换关联函数和进行截断能测试时,3种硫铁矿都采用单胞模型,黄铁矿采用4×4×4的K点网络,白铁矿采用4×4×6的K点网络, 磁黄铁矿采用4×4×2的K点网络。几何优化采用BFGS算法,优化参数如下:原子最大位移的收敛标准设为0.000 2 nm;原子间作用力的收敛标准设为0.8 eV/nm;原子间内应力的收敛标准设为0.1 GPa;体系总能量变化的收敛标准设为2.0×10−5eV/atom;自洽场收敛精度设为2.0×10−6eV/atom;参与计算的原子轨道为Fe原子 3d64s2,S原子 3s23p4。所有性质的计算都采用与几何优化相同的参数,计算态密度时采用的smearing值为0.1 eV。另外,采用Dmol3软件[20]对已优化的晶胞再进行能量优化,K点选择 Gamma点,计算矿物的前线轨道性质,双黄药和氧气的分子结构优化及前线轨道性质的计算也采用 Dmol3软件来完成。所选取的参数如下:交换关联函数采用GGA-PW91,使用有效核势及 DNP基组,精度设为fine;自洽场收敛标准设为 1.0×10−6eV/atom。以上所有计算都采用自旋极化,并且都在倒易空间中进行。

表2 3种硫铁矿的截断能测试结果Table 2 Results of cutoff energy tests of three sulfurous iron minerals
1.2 计算模型
选择具有代表性的硫铁矿晶体结构为研究对象。黄铁矿具有立方晶体结构,空间对称结构为分子式为FeS2,属于等轴晶系,铁原子位于单胞的6个面心及8个顶角上,每个铁原子与6个相邻的硫配位,而每个硫原子与3个铁原子和1个硫原子配位,2个硫原子之间形成哑铃状结构,以硫二聚体(S22−)形式存在,且沿着〈111〉方向排列。白铁矿的空间对称结构为 Pnnm,分子式为 FeS2,属于斜方晶系,铁原子位于单胞的体心及8个顶角,每个铁原子与6个相邻的硫配位,而每个硫原子与3个铁原子和1个硫原子配位,哑铃状对硫离子之轴向与c轴相斜交,而它的两端位于铁离子2个三角形的中点。磁黄铁矿的空间对称结构为 P3(1)21,分子式为 Fe21S24,属于高温六方晶系,铁原子的配位情况有3种:每个铁原子与6个相邻的硫原子形成六配位;每个铁原子与6个相邻的硫原子和1个相邻的铁原子形成七配位;每个铁原子与6个相邻的硫原子和2个相邻的铁原子形成八配位。硫原子的配位情况有2种:每个硫原子与5个铁原子形成五配位;每个硫原子与6个铁原子形成六配位。黄铁矿、白铁矿和磁黄铁矿的单胞模型如图1所示。
2 计算结果与讨论
2.1 能带结构及态密度分析
黄铁矿、白铁矿和磁黄铁矿的能带结构如图2所示,取费米能级(ΕF)作为能量零点。计算结果表明,黄铁矿为直接带隙型半导体,计算所得的带隙值为0.58 eV,低于实验值(0.95 eV)[13];白铁矿为间接带隙半导体,间接带隙理论计算值为0.98 eV,高于实验值(0.40 eV)[15](带隙值高于或低于实验值主要是GGA近似下的 DFT对电子与电子之间的交换关联作用处理不足引起的[21]);磁黄铁矿的导带和价带相交,属于导体。从能带结构计算结果可知,黄铁矿和白铁矿属于窄能隙半导体,而磁黄铁矿属于金属导体,因此,它们在浮选过程中与药剂的电化学反应具有很大的差异。
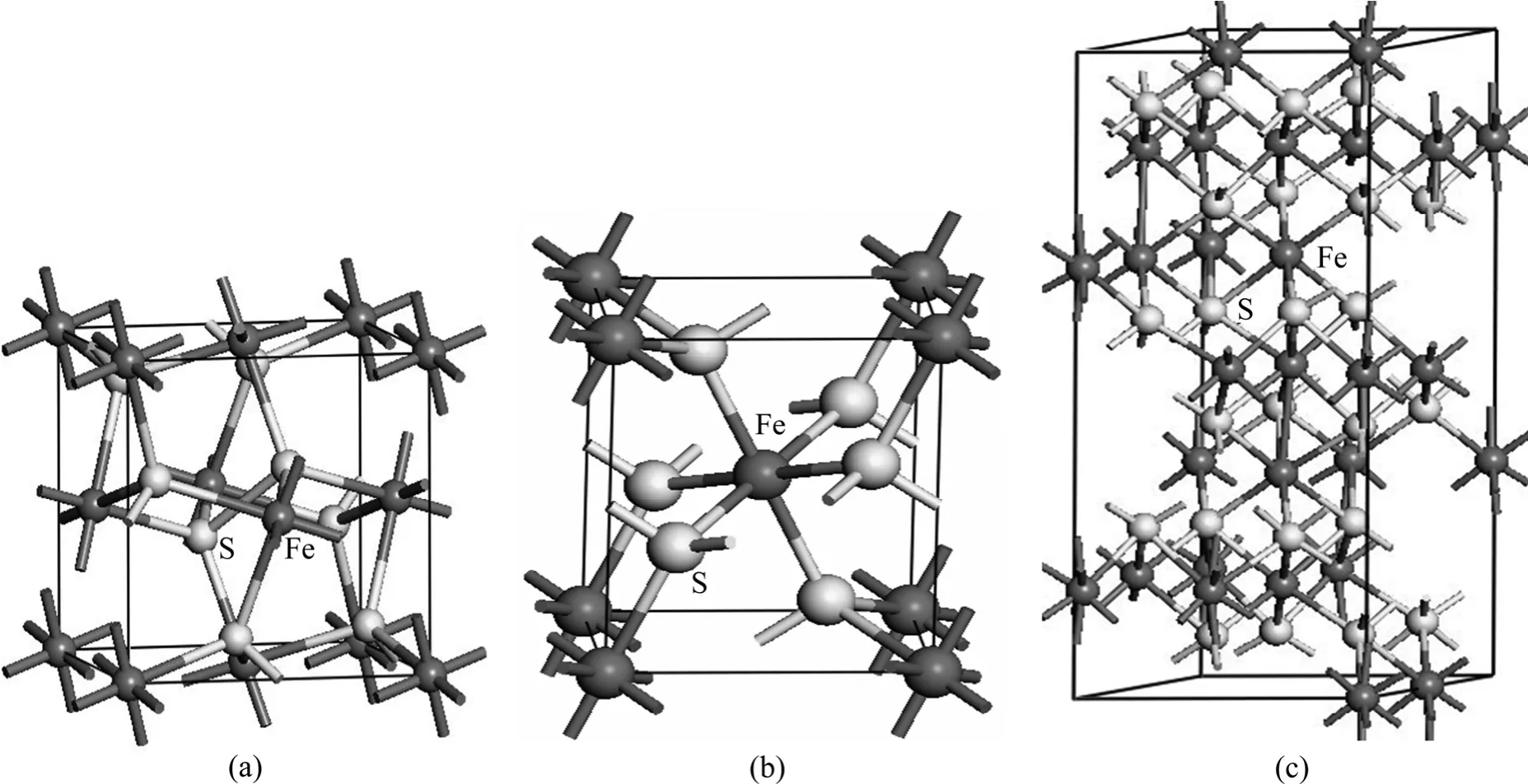
图1 黄铁矿、白铁矿和磁黄铁矿的单胞模型Fig.1 Unit cell models of pyrite (a), marcasite (b) and pyrrhotite (c)
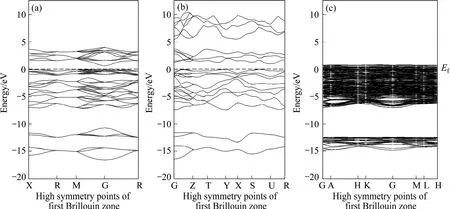
图2 黄铁矿、白铁矿和磁黄铁矿的能带结构Fig.2 Band structures of pyrite (a), marcasite (b) and pyrrhotite (c)
黄铁矿的态密度如图3所示。从图3可知:黄铁矿的能带在−17~5 eV范围内分为5部分,在−17~−10 eV间的两组价带几乎全部由硫原子的3s轨道组成,仅有少部分硫原子的 3p轨道贡献;价带顶以下−7.5~−1.5 eV范围内的价带由硫原子的3p轨道和铁原子的3d轨道共同组成,贡献最大的是硫原子的3p轨道;顶部价带主要由硫原子的3p轨道和铁原子的3d轨道组成,且大部分贡献来自铁原子的3d轨道来;导带能级主要由硫原子的3p轨道和铁原子的3d轨道共同组成,仅有少量硫原子的3s轨道和铁原子的3p轨道贡献;此外,铁原子的4s轨道对态密度的贡献非常小。费米能级附近的态密度主要由铁原子的 3d轨道构成。
白铁矿的态密度如图4所示。从图4可以看出,在−17~−11.5 eV之间的两组价带几乎全部由硫原子的3s轨道贡献,还有少量硫原子的3p轨道贡献;价带顶即费米能级以下的态密度,主要由硫原子的3p轨道和铁原子的3d轨道共同组成;0.5~4 eV范围内的导带主要由硫原子的3p轨道和铁原子的3d轨道共同组成;5~11 eV之间的导带由铁原子的4s轨道和铁原子的3p轨道共同组成,还有少部分来自硫原子 3p轨道的贡献。费米能级附近的态密度主要由铁原子的 3d轨道构成。
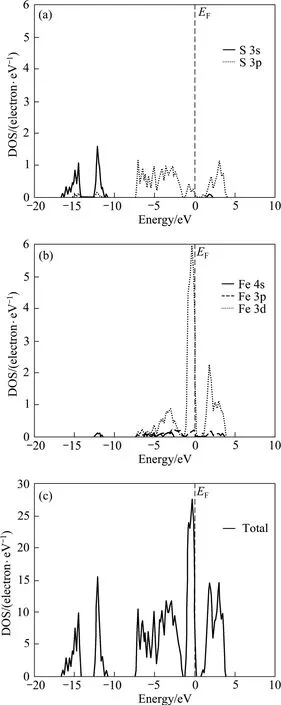
图3 黄铁矿的态密度Fig.3 Density of state (DOS) of pyrite
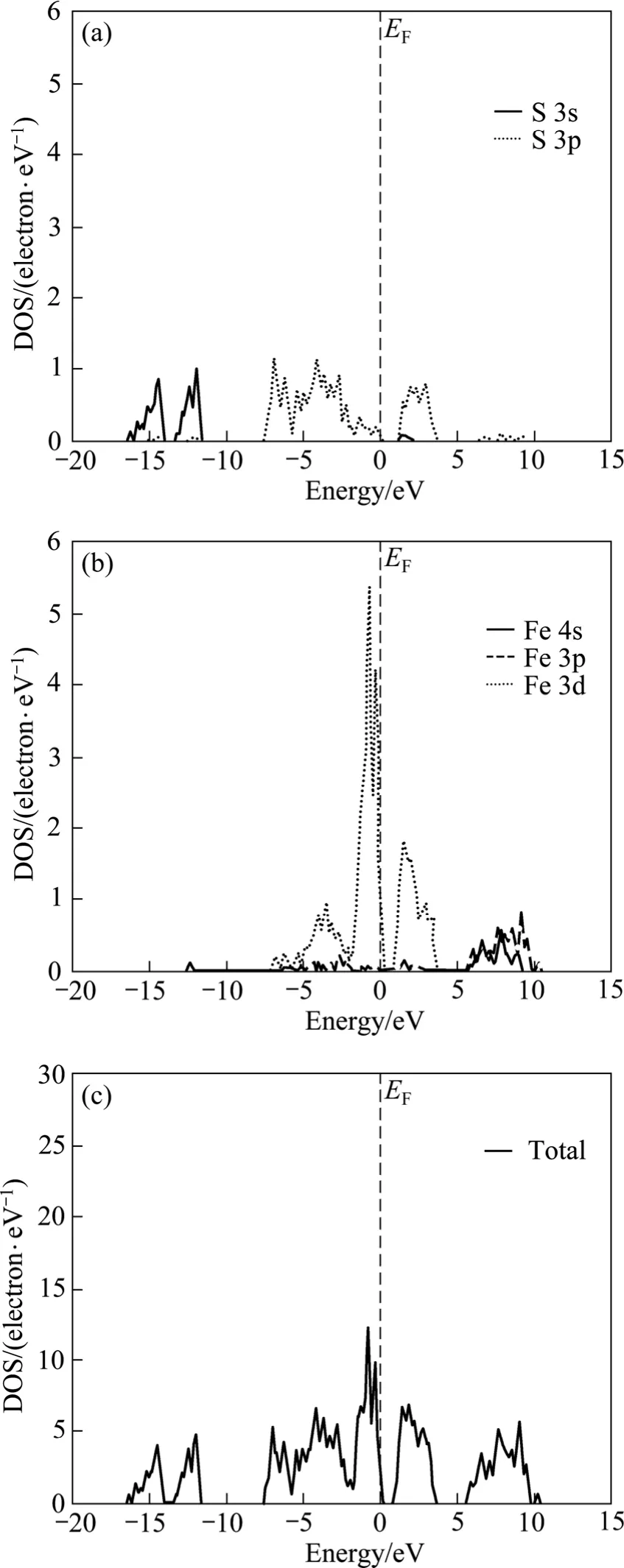
图4 白铁矿的态密度Fig.4 DOS of marcasite
图5 所示为磁黄铁矿的态密度图。从图5可以看出,磁黄铁矿的能带由两部分构成,位于−15~−12 eV范围内的价带几乎全部由硫原子的 3s轨道贡献;从−7.5~2.5 eV之间的能带大部分由硫原子的3p轨道和铁原子的3d轨道贡献,还有极少量来自铁原子4s轨道和铁原子3p轨道的贡献。 费米能级附近的态密度主要由铁原子的 3d轨道构成,还有由少量硫原子的3p轨道构成。

图5 磁黄铁矿的态密度Fig.5 DOS of pyrrhotite
黄铁矿、白铁矿和磁黄铁矿的自旋态密度如图 6所示。由图6可以看出,黄铁矿和白铁矿为低自旋态,而磁黄铁矿为自旋−极化态,费米能级附近的自旋态密度主要由铁原子的3d轨道贡献。 与低自旋态的黄铁矿和白铁矿相比,自旋−极化态的磁黄铁矿更容易与磁性类物质如氧气发生反应,因此,磁黄铁矿容易被氧化,这与自然界中磁黄铁容易被氧化的实际相符。
费米能级附近的电子活性最强,因此,通过分析费米能级附近的电子态密度组成可以知道原子的反应活性。由态密度分析可知,3种硫铁矿中的铁原子的3d轨道主要对费米能级附近的态密度作贡献,但贡献的大小不同。其中,费米能级附近铁原子的3d轨道电子最活跃、贡献最大的是黄铁矿,其次是白铁矿,而磁黄铁矿中的铁原子的贡献最小。因此,黄铁矿的铁最活跃,磁黄铁矿中的铁活性最低,在浮选过程中,黄铁矿最容易与氢氧根和氰离子作用,而磁黄铁矿的作用较弱。
2.2 Mulliken布居分析
2.2.1 原子的Mulliken布居分析
黄铁矿、白铁矿和磁黄铁矿的硫原子和铁原子在优化前的价电子构型分别为S 3s23p4和Fe 3d64s2,优化后原子的Mulliken布居值如表3所列。从表3可知,黄铁矿优化后的价电子构型为 S 3s1.803p4.12、Fe 3p0.643d7.174s0.35,硫原子为电子供体,主要是硫原子的3s轨道失去电子,定域在硫原子的电子数为5.92,失去0.08个电子,硫原子所带电荷为+0.08 e;铁原子为电子受体,主要是铁原子的3d轨道得到电子,定域在铁原子的电子数为8.16,得到0.16个电子,Fe原子所带电荷为−0.16 e。
白铁矿优化后的构型为 S 3s1.813p4.14和 Fe 3p0.603d7.144s0.36,定域在硫原子的电子数为5.95,失去0.05个电子,硫原子所带电荷为+0.05 e,为电子供体,主要是硫原子的3s轨道失去电子;定域在铁原子的电子数为 8.10,得到 0.10个电子,铁原子所带电荷为−0.10 e,为电子受体,主要是铁原子的3d轨道得到电子。
磁黄铁矿优化后的构型为 S 3s1.823p4.39和 Fe 3p0.653d6.694s0.42,硫原子为电子受体,主要是硫原子的3p轨道得到电子,定域在硫原子的电子数为6.21,得到0.21个电子,硫原子所带电荷为−0.21 e;Fe原子为电子供体,主要是铁原子的3s轨道失去电子,定域在铁原子的电子数为7.76,失去0.24个电子,铁原子所带电荷为+0.24 e。黄铁矿和白铁矿中的铁原子带负电,硫原子带正电,而磁黄铁矿中铁原子带正电,硫原子带负电,说明黄铁矿和白铁矿中铁−硫的共价性较强,而由于硫−硫之间成键,导致电子云向铁偏移。磁黄铁矿中硫原子之间不成键,导致铁−硫之间离子性成分增加,从而使铁带正电。
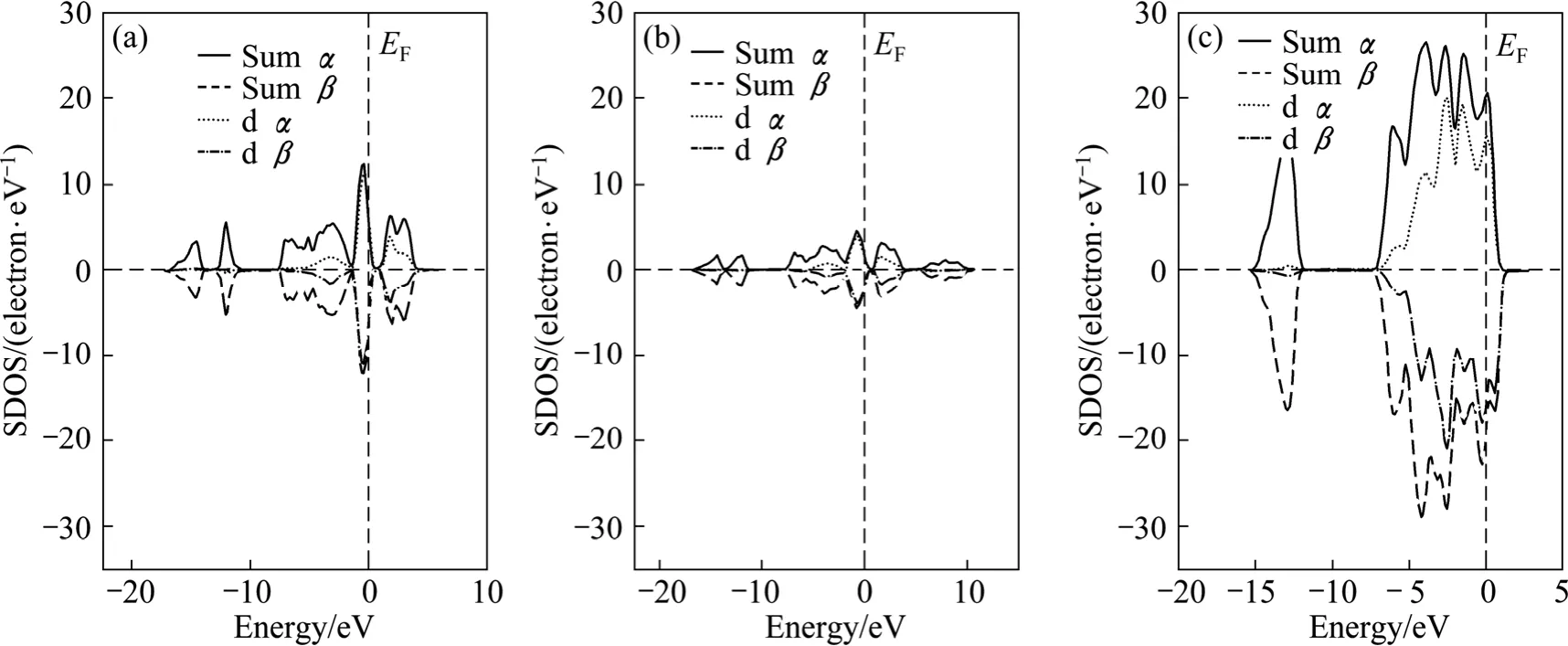
图6 黄铁矿、白铁矿和磁黄铁矿的自旋态密度Fig.6 Spin density of state (SDOS) of pyrite (a), marcasite (b) and pyrrhotite (c)
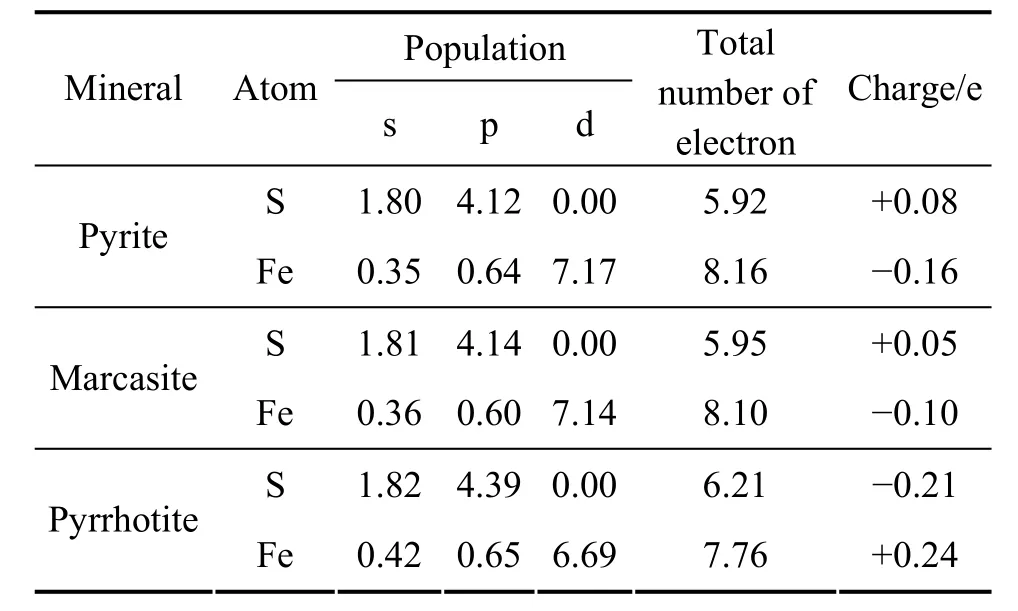
表3 黄铁矿、白铁矿和磁黄铁矿原子的Mulliken布居分析Table 3 Mulliken atomic population analysis of pyrite,marcasite and pyrrhotite
2.2.2 3种硫铁矿中键的Mulliken布居分析
键的Mulliken布居值体现键的离子性和共价性的强弱,布居值大,表明原子间的结合为共价键,反之则为离子键。黄铁矿、白铁矿和磁黄铁矿中键的Mulliken布居值列于表4。由表4数据分析可知,黄铁矿中Fe—S的共价性大于S—S的,Fe—S的键长比S—S的稍短。白铁矿Fe—S的布居值为0.28和0.66,大于 S—S的(0.08),说明 Fe—S的共价性大于 S—S的, Fe—S和S—S的键长比较接近。而磁黄铁矿中键的布居比较复杂,Fe—S键的布居值为0.11~0.44,Fe—Fe的布居值为−0.11~−0.20,Fe—S 的共价性大于Fe—Fe的,Fe—S的键长为0.227 1~0.290 5 nm,Fe—Fe的键长为0.281 2~0.297 2 nm。
由Mulliken布居分析可以看出,黄铁矿与白铁矿晶体内部的Fe—S之间主要以共价性为主,且共价性相近,但白铁矿中S—S之间的共价性弱于黄铁矿的,磁黄铁矿晶体内部键之间由于铁原子之间成键,呈现出较大的离子性。因此,在浮选过程中,共价性较强的黄铁矿和白铁矿具有较好的疏水性,而离子性较强的磁黄铁矿的疏水性较弱。

表4 黄铁矿、白铁矿和磁黄铁矿中各键的 Mulliken布居分析Table 4 Mulliken bond population analysis of pyrite,marcasite and pyrrhotite
2.3 前线轨道分析
福井谦一提出了前线轨道理论,认为分子的许多性质主要由分子中的前线轨道决定,即最高占据分子轨道(Highest occupied molecular orbital, HOMO)和最低空轨道(Lowest unoccupied molecular orbital, LUMO)决定[22]。根据前线轨道理论,一个反应物的 HOMO与另一个反应物的 LUMO的能量值之差的绝对值(|ΔΕ|)越小,两分子之间的相互作用就越强。对于硫铁矿,参与反应的是黄药的 HOMO轨道和硫铁矿的LUMO轨道,以及氧气的 LUMO轨道和硫铁矿的HOMO轨道。
3种硫铁矿及药剂的前线轨道能量列于表5。 由表 5可知,磁黄铁矿与氧分子作用的前线轨道能量|ΔΕ1|最小(0.417 eV),其次为白铁矿的(1.054 eV),黄铁矿与氧分子作用的|ΔΕ1|最大(1.685 eV),说明磁黄铁矿与氧分子的作用最强,白铁矿次之,黄铁矿与氧分子的作用最弱。3种硫铁矿的被氧化由易到难的顺序为磁黄铁矿,白铁矿,黄铁矿,这与文献报道和实际结果一致[2]。从氧气的分子轨道分析可知,氧气分子中有2个孤对电子分别排布在2个反键π轨道上,所以,氧气分子具有顺磁性;而由自旋态密度分析比较可知,黄铁矿和白铁矿为低自旋态,而磁黄铁矿则为自旋−极化态,因此,在这 3种硫铁矿中,氧分子更容易与自旋−极化态的磁黄铁矿发生作用。当矿石存在磁黄铁矿时,由于氧气会优先与磁黄铁矿反应,消耗了矿浆中大量的氧,导致其他硫化矿物不被浮选,只有当充分搅拌充气后,矿浆中有剩余氧气时,才能浮选其他矿物[23]。

表5 矿物及药剂的前线轨道能量Table 5 Frontier orbital energy of minerals and reagents
黄药在白铁矿、黄铁矿和磁黄铁矿这3种矿物表面的产物都是双黄药[3],浮选实验结果表明,黄药捕收这3种硫铁矿的可浮性由强到弱的顺序如下:白铁矿,黄铁矿,磁黄铁矿[1]。从表 5可见,黄铁矿与黄药作用的前线轨道能量|ΔΕ2|最大(0.708 eV),其次为白铁矿的(0.420 eV),磁黄铁矿与黄药作用的|ΔΕ2|最小(0.228 eV),说明黄药与白铁矿的作用大于黄铁矿的,因此,白铁矿的可浮性大于黄铁矿的;而对于磁黄铁矿,虽然它与黄药的作用最强,但在含有氧气的浮选体系中,由于磁黄铁矿极易与氧气发生作用,导致磁黄铁矿过度氧化,在其表面生成可溶性薄膜,不利于双黄药的吸附,因此,在含氧浮选体系中磁黄铁矿的可浮性比白铁矿和黄铁矿的差。
3 结论
1) 黄铁矿为直接带隙半导体,白铁矿为间接带隙半导体,而磁黄铁矿为导体。
2) 黄铁矿和白铁矿为低自旋态,而磁黄铁矿则为自旋−极化态。
3) 用前线轨道理理论解释了 3种硫铁矿被氧化由易到难的顺序为磁黄铁矿,白铁矿,黄铁矿。
4) 用前线轨道理理论解释了 3种硫铁矿用黄药捕收可浮性由强到弱的顺序为白铁矿,黄铁矿,磁黄铁矿。
REFERENCES
[1] 胡为柏. 浮选[M]. 北京: 冶金工业出版社, 1989: 273−274.HU Wei-bo. Floatation[M]. Beijing: Metallurgical Industy Press,1989: 273−274.
[2] 原田种臣. 氧化对黄铁矿, 白铁矿和磁硫铁矿浮游性的影响[J]. 国外金属矿, 1965, 11: 16−20.YUAN-TIAN Zhong-chen. The effects of oxidation on the floatability of pyrite, marcasite and pyrrhotite[J]. Metallic Ore Dressing Abroad, 1965, 11: 16−20.
[3] 陈建华, 冯其明, 卢毅屏. 电化学调控浮选能带理论及应用(Ⅱ)—黄药与硫化矿物作用的能带模型[J]. 中国有色金属学报, 2000, 10(3): 426−430.CHEN Jian-hua, FENG Qi-ming, LU Yi-ping. Energy band model of elctrochemical flotation and its application(Ⅱ)—Energy band model of xanthate interacting with sulphide minerals[J]. The Chinese Journal of Nonferrous Metals, 2000,10(3): 426−430.
[4] 陈建华, 冯其明, 卢毅屏. 电化学调控浮选能带理论及应用(I)—半导体−溶液界面能带理论及模型[J]. 中国有色金属学报,2000, 10(2): 240−242.CHEN Jian-hua, FENG Qi-ming, LU Yi-ping. Energy band model of electrochemical flotation and its application(I)—Theory and model of energy band of semiconductor-solution interface[J]. The Chinese Journal of Nonferrous Metals, 2000,10(2): 240−242.
[5] CHEN Ye, CHEN Jian-hua. The first-principle study of the effect of lattice impurity on adsorption of CN on sphalerite surface[J].Miner Eng, 2010, 23(9): 676−684.
[6] CHEN Jian-hua, CHEN Ye, LI Yu-qiong. Effect of vacancy defects on electronic properties and activation of sphalertite(110)surface by first-principles[J]. Transactions of Nonferrous Metals Society of China, 2010, 20: 502−506.
[7] CHEN Jian-hua, CHEN Ye. A first-principle study of the effect of vacancy defects and impurity on adsorption of O2on sphalerite surface[J]. Colloids and Surface A: Physiochem Eng Aspects, 2010, 363(1/3): 56−63.
[8] EDELBRO R, SANDSTR Ö M Å, PAUL J. Full potential calculations on the electron band structures of sphalerite, pyrite and chalcopyrite[J]. Appl Surf Sci, 2003, 206(1/4): 300−313.
[9] von OERTZEN G U, JONES R T, GERSON A R. Electronic and optical properties of Fe, Zn and Pb sulfides[J]. J Electron Spectrosc, 2005, 144/147(6): 1245−1247.
[10] 李玉琼, 陈建华, 陈 晔. 空位缺陷黄铁矿的电子结构及其浮选行为[J]. 物理化学学报, 2010, 26(5): 1435−1441.LI Yu-qiong, CHEN Jian-hua, CHEN Ye. Electronic structures and flotation behavior of pyrite containing vacancy defects[J].Acta Phys-Chim Sin, 2010, 26(5): 1435−1441.
[11] MARZARI N, VANDERBILT D, PAYNE M C. Ensemble density-functional theory for ab-initio molecular dynamics of metals and finite-temperature insulators[J]. Phy Rev Lett, 1997,79(7): 1337−1340.
[12] PRINCE K C, MATTEUCCI M, KUEPPER K, CHIUZBAIAN S G, BARKOWSKI S, NEUMANN M. Core-level spectroscopic study of FeO and FeS2[J]. Phys Rev B, 2005, 71: 085102.
[13] SCHLEGEL A, WACHTER P. Optical properties, phonons and electronic structure of iron pyrite (FeS2) [J]. J Phys C: Solid State Phys, 1976, 9: 3363−3369.
[14] RIEDER M, CRELLING J C, SUSTAI O, DRABEK M, WEISS Z, KLEMENTOVA M. Arsenic in iron disulfides in a brown coal from the North Bohemian Basin, Czech Republic[J]. Int J Coal Geology, 2007, 71: 115−121.
[15] UHLIG I, SZARGAN R, NESBITT H W, LAAJALEHT K.Surface states and reactivity of pyrite and marcasite[J]. Appl Surf Sci, 2001, 179: 222−229.
[16] CHIVCHAGOV A V. Information-calculating system on crystal structure data of minerals(MINCRYST)[J]. Mater Sci Forum,1994, 166/169: 193−198.
[17] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple[J]. Phy Rev Lett, 1996,77(18): 3865−6868.
[18] VANDERBILT D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism[J]. Phys Rev B, 1990, 41(11):7892−7895.
[19] PACK J D, MONKHORST H J. Special points for Brillouin-zone integrations—A reply[J]. Phys Rev B, 1977,16(4): 1748−1749.
[20] JONES R O, GUNNARSSON O. The density functional formalism, its application and prospects[J]. Rev Mod Phys, 1989,61(3): 689−746.
[21] ANISIMOV V I, ARYASETIAWAN F, LICHTENSTEIN A I.First-principles calculations of the electronic structure and spectra of strongly correlated systems: The LDA+ U method[J].J Phys: Condens Matter, 1997, 9(4): 767−808.
[22] MICHAEL J S, DEWAR S. A critique of frontier orbital theory[J]. Journal of Molecular Structure: Theochem, 1989, 20:301−323.
[23] 崔毅琦, 童 雄, 周庆华, 何 剑. 国内外磁黄铁矿浮选的研究概况[J]. 金属矿山, 2005, 347: 24−26.CUI Yi-qi, TONG Xiong, ZHOU Qin-hua, HE Jian. Survey of research on pyrrhotite flotation both at home and abroad[J]. Met Mine, 2005, 347: 24−26.
Electronic structures and floatability of pyrite, marcasite and pyrrhotite
CHEN Jian-hua1, ZHONG Jian-lian1, LI Yu-qiong2, CHEN Ye1, GUO Jin3
(1. College of Resources and Metallurgy, Guangxi University, Nanning 530004, China;2. College of Chemistry and Chemical Engineering, Guangxi University, Nanning 530004, China;3. College of Physics Science and Engineering, Guangxi University, Nanning 530004, China)
The electronic structures of pyrite, marcasite and pyrrhotite were calculated using the first-principles method which was based on the density functional theory (DFT), and the relationship between the electronic structure and floatability of the three sulfurous iron minerals was discussed. The calculation results show that pyrite is a direct band-gap semiconductor, and marcasite is an indirect band-gap semiconductor, while pyrrhotite is a conductor. The density of state analysis reveals that pyrite and marcasite are in low spin state, while pyrrhotite is in spin-polarized state.In addition, the calculation of the frontier orbital indicates that the oxidized order of the three sulfurous iron minerals from easy to difficult is as follows: pyrrhotite, marcasite, pyrite, and the floatability order of the three sulfurous iron minerals from easy to difficult using xanthate as a collector is as follows: marcasite, pyrite, pyrrhotite. The interaction between the three sulfurous iron minerals and oxygen, and the floatability of the three sulfurous iron minerals collected by xanthate can be well explained by the calculation results.
pyrite; marcasite; pyrrhotite; electronic structure; floatability; density functional theory
TD923.13
A
1004-0609(2011)07-1719-09
国家自然科学基金资助项目(50864001)
2010-08-16;
2010-11-06
陈建华,教授,博士:电话:0771-3232200; E-mail: jhchen@gxu.edu.cn
(编辑 陈卫萍)
