环件热辗扩成形有限元建模仿真研究进展

王 敏, 杨 合, 郭良刚

环件热辗扩成形有限元建模仿真研究进展

王 敏1,2, 杨 合2, 郭良刚2

(1. 湖北汽车工业学院 材料工程系，十堰 442002；2. 西北工业大学 材料科学与工程学院 凝固技术国家重点实验室，西安 710072)

环件热辗扩成形问题是多场、多因素耦合作用下集三维连续渐变、非稳态及非对称等特点于一体的高度非线性问题，采用有限元建模仿真方法研究与发展该技术对实现无缝环形构件的高质量、低成本及短周期制造具有重要意义。分别从宏观和微观尺度评述环件热辗扩成形有限元建模仿真的国内外研究现状、存在的问题与发展趋势，进而指明其发展方向如下：大型、复杂环件径、轴双向热辗扩成形全过程自适应建模的仿真方法与关键技术；环件热辗扩成形过程宏观与微观有限元建模仿真无缝集成技术；适用于以环件热辗扩为代表的连续局部塑性成形过程的材料本构模型和组织演变模型以及相应稳健而高效的有限元算法、本构积分算法与组织演变仿真方法；考虑模具的变形、传热及主要失效形式的环件热辗扩成形过程建模仿真技术。

环件热辗扩；微观组织；建模；仿真；有限元

环件热辗扩成形是用于制造无缝环形零件的连续局部塑性成形先进技术，它利用轧辊的旋转和直线进给运动对高温环件进行连续、局部施压，使环件在回转过程中壁厚减小、直径扩大、截面轮廓成形(见图1)[1]。环件热辗扩成形由于可以满足环件对精确、高效、节能和数字化制造要求，已逐步取代了自由锻、马架扩孔和弯焊等传统的环件生产工艺，成为无缝环件的首选和主要的成形技术。该技术的研究和发展既是航空航天等高技术领域发展的迫切需求，又是环件制造向先进塑性成形技术发展的必然趋势[2−3]。

图1 环件热辗扩成形示意图[1]Fig.1 Schematic diagram of hot ring rolling[1]

然而，该过程是集三维连续渐变、非对称、非稳态、宏微观耦合与热力耦合等特点于一体的高度非线性问题，材料在该过程中经历多场、多因素耦合作用下复杂、多道次局部加载与卸载、不均匀塑性变形和微观组织演化历程，这使得对该过程的研究成为一个具有挑战性的难题。由于问题的复杂性，基于理论解析、经验和反复试验的方法难以满足对该过程精确、高效和全方位研究以及数字化、高技术化发展的需求，而有限元建模仿真能虚拟成形过程，将大量反复试验在计算机上完成，已成为研究与发展先进精确塑性成形技术，高质量、低成本、短周期、自主创新地实现塑性成形产品开发的强有力工具[2,4]，为解决环件热辗扩这种典型的复杂塑性成形问题创造了有利条件。

本文作者分别从宏观和微观尺度综述环件热辗扩成形有限元建模仿真的国内外研究现状、存在的问题与发展趋势，进而指明其重点发展方向。

1 环件热辗扩成形宏观有限元建模仿真

有限元方程有两种求解算法，即静力隐式算法(简称隐式算法)和动力显式算法(简称显式算法)。这两种算法均可用于环件热辗扩成形问题的求解，以下将分别进行讨论。

1.1 隐式建模仿真

隐式算法较早用于求解包括环件热辗扩成形在内的塑性成形问题，是目前塑性加工界广泛采用的一种算法[5]。隐式算法采用迭代法求解方程，是无条件稳定的，其计算结果较为精确，能求解大多数塑性成形问题。然而，对于环件热辗扩这类具有复杂接触边界条件的连续、局部塑性成形问题，采用此法进行求解的难度较大，这是由此类问题的成形特征所决定的。对于环件热辗扩成形，隐式算法的求解难点主要体现以下4个方面：

1) 相对于环件总尺寸，变形区非常小，为了有效模拟变形区内环件和轧辊之间的接触状况及金属填充孔型情况，环件的网格必须细化，但这会导致单元和节点数的剧增，对于大型环件或复杂环件尤为突出。

2) 轧辊与环件的接触边界条件不仅动态变化，而且环件横截面上不同直径处的接触边界条件不同，加之材料非线性的大变形行为，此多重非线性导致隐式算法所允许时间增量步长的显著缩短，甚至无法收敛。

3) 环件每转进给量较小，因此，环件需要旋转很多圈才能获得所需的变形量，从而导致隐式算法时间增量步数的增多。

4) 成形过程中变形区的形状和大小不断发生变化，因此，该过程是非稳态的，其隐式模拟仿真的时间增量步长比板带材轧制等稳态成形过程的短。

综上所述，环件热辗扩的连续、局部、回转、小增量及非稳态等成形特征使得采用隐式算法求解该问题需要大量的单元和时间增量，且动态接触边界条件和热力耦合效应使求解不易收敛，因此，该问题的求解需要耗费大量机时。迄今为止，各国学者力图运用各种方法和技术来提高该问题的求解效率，这些方法和技术可分为以下几类。

1.1.1 简化模型

1) 维数缩减或仅考虑变形区的三维建模

YANG 和 KIM[6]最早采用有限元模拟环件热辗扩成形过程。他们将该过程简化成平面应变问题，仅针对变形区建立了刚塑性有限元模型，通过该模型获得了变形区的速度场、应变速率场及接触面的压力分布等。SONG等[7]也将环件热辗扩简化为平面应变问题，基于Mark/Mentat平台，运用弹塑性热力耦合有限元分析了IN718高温合金环件的几何形状变化、应力、应变和温度分布及辗扩力等。

TSZENG 和 ALTAN[8]采用伪平面应变有限元对T型环件热辗扩成形过程进行了分析。WARD等[9]基于伪平面应变假设实现了火车车轮和轮毂的热辗扩成形有限元模拟。JOUN等[10]将金属流动近似为伪平面应变模式，将成形过程视为一系列连续锻造过程，采用刚粘塑性有限元对轴承座圈热辗扩成形进行了模拟。

尽管采用二维有限元法模拟环件辗扩成形过程的计算效率高，但与实际不符，精度难以保证，而且不能模拟宽展、轴向锥辊等。因此，环件热辗扩成形过程的三维有限元建模仿真越来越受到国内外学者的重视。

XU 等[11]针对变形区，基于稳态假设，建立了碳钢环热辗扩成形过程热力耦合三维刚粘塑性有限元模型，获得了力能参数与热力学参数的分布。XU等[12]和许思广等[13−14]对矩形和异型碳钢环热辗扩成形过程中金属流动和场量分布规律进行了研究；许思广等[15]根据环件热辗扩成形的特点，分别建立了变形区内的稳态温度模型和变形区外的瞬态温度模型，并将两个模型集成为整体模型，将该整体模型与变形区三维刚塑性有限元模型相耦合，用于预测环件内部的温度分布和变化。YANG等[16]针对变形区，建立了T型环件热辗扩成形过程三维刚塑性有限元模型，揭示了碲铅合金和铝合金环件的金属轴向流动特性和截面充填规律。KIM 等[17]针对变形区，运用 Superform软件建立了合金钢大型异型环件热辗扩成形三维有限元模型，并采用此模型模拟了金属填充孔型过程及应变和宽展分布。

针对变形区的三维建模，通过减少单元和节点数来达到提高隐式模型求解效率的目的，这不可避免地会产生一些负面效应，比如求解精度不高，不能考虑变形区外金属的变形及其与变形区内金属变形的相互影响、环件的圆度、过程的稳定性以及导向辊和轴向锥辊的作用等。

2) 忽略导向辊的建模

上述绝大部分简化模型均忽略了导向辊，这主要起因于以下两方面：一是导向辊建模较为复杂，不仅要增加接触表面，而且要细分接触表面的网格，并且在成形过程中导向辊的具体位置及其与环件之间的作用力都是未知的；二是导向辊与环件之间的作用力较小，因此，忽略导向辊并不会对成形过程造成严重的影响[18]。然而，为了更真实地反映实际情况，一些学者通过各种途径将导向辊引入环件辗扩成形过程的有限元模型中。HU等[19]采用两个无摩擦的圆柱形壳体来模拟导向辊，导向辊的运动轨迹根据环件体积不变原理和无宽展假设近似得到。GUO等[20]采用类似的方法建立了导向辊模型，并研究了导向辊对成形过程稳定性和环件圆度的影响，发现如果忽略导向辊，环件则可能产生剧烈摆动和“多边形”缺陷，该研究表明导向辊对成形过程的作用并不能忽略。LIM 等[21]和WANG等[22]通过前一增量步有限元计算得到了环件的瞬时外径，然后，利用环件与导向辊的方位关系来确定导向辊的运动轨迹。

上述基于运动轨迹的导向辊建模方法尽管简单，易于实现，也便于在不同软件平台之间移植，但它只适用于小型和简单截面环件辗扩成形过程。因此，一些学者相继提出了各种适应性更广的导向辊建模方法。XIE等[23]用两个有摩擦的圆柱形实体代表导向辊，模拟过程中一旦发现环件表面节点渗入导向辊表面，就在渗入的环件表面节点上施加惩罚力来模拟导向辊对环件的压力。DAVEY和WARD[24]采用任意拉格朗日－欧拉技术，通过在位于环件径向平面上的一些环件节点上施加特殊的边界条件来模拟导向辊的作用。FOROUZAN 等[25−26]基于ANSYS软件平台，采用“热辐条法”将导向辊引入环件热辗扩成形有限元模型中，该方法中不需要导向辊运动轨迹的计算，不会给模型增加额外的非线性，并且在不引入额外单元的情况下还可以考虑导向辊臂的刚度。他们采用该方法研究了导向辊对环件摆动、环件与轧辊的接触区域及力能参数等的作用，结果表明，导向辊通过对接触区域的影响而对整个成形过程产生重要影响，进一步验证了文献[20]的观点。LI等[27]以 ABAQUS为平台建立了导向辊液压调节机构，该机构利用导向辊和环件之间的接触压力来对导向辊的运动进行自适应柔性控制，这是目前与实际情况最接近的导向辊建模方法。然而，相对于基于运动轨迹的导向辊建模方法，这些建模方法较复杂，且不便于在不同软件平台之间移植。

由上述研究结果可知，尽管导向辊对环件的作用力较小，但其对环件热辗扩成形过程的稳定性及环件的圆度有重要影响，对大型环件热辗扩成形更是如此，因此，在成形过程的建模仿真中不应忽略导向辊。

3) 忽略芯辊和环件之间摩擦的建模

与忽略导向辊所起的作用相同，忽略芯辊和环件之间的摩擦也可以提高隐式模型的收敛性和计算效率，这是因为芯辊在成形过程中不承受转矩，在其与环件之间摩擦力的带动下自由转动，其转速是未知的，故计算摩擦力非常困难。YANG 和 KIM[16]在不同摩擦条件下对变形区内的等效应变速率分布进行比较后发现，这些模拟结果较为相似，由此认为芯辊和环件之间的零摩擦假设是合理的。HU 和LIU[28]对摩擦因数为0、0.2和0.5条件下的模拟结果进行对比后发现，3种摩擦条件下的模拟结果很接近，这进一步支持了零摩擦假设的有效性。零摩擦假设后来陆续被 HU等[19]和LIM等[21]所沿用。然而，DAVEY和WARD[29]在无摩擦、仅沿环件轴向有摩擦和沿环件任何方向都有摩擦 3种情况下，对比轴向宽展的情况后发现，3种情况下的宽展虽然具有相同的变化趋势，但数值上存在差别，尤其在无摩擦和沿环件任何方向都有摩擦两种情况下宽展的差异较大。该研究表明，考虑芯辊和环件之间的摩擦有助于获得更精确的模拟结果。

1.1.2 双网格(Dual-mesh)技术

KIM 等[30]最早采用三维有限元法和双网络技术对完整环件热辗扩成形过程进行了模拟。双网格技术包含两个网格系统(见图2)，即计算网格和材料网格。材料网格用于存贮节点和单元变量值，在整个环件上均匀、细密地分布，其位置固定在环件材料上，随环件而运动。而计算网格是实际有限元运算时所使用的网格，它在变形区内较细密，在变形区外较稀疏，且没有沿环件周向的旋转运动。在每个时间增量步结束后，计算网格将此步计算所得新的变量值以一定的插值算法传递给材料网格，系统根据材料网格中存贮的变量值来更新环件几何。在下一个时间增量步开始时，材料网格又将其更新后的几何传递给计算网格。双网格技术减少了计算时环件的单元数，缩短了计算机时。

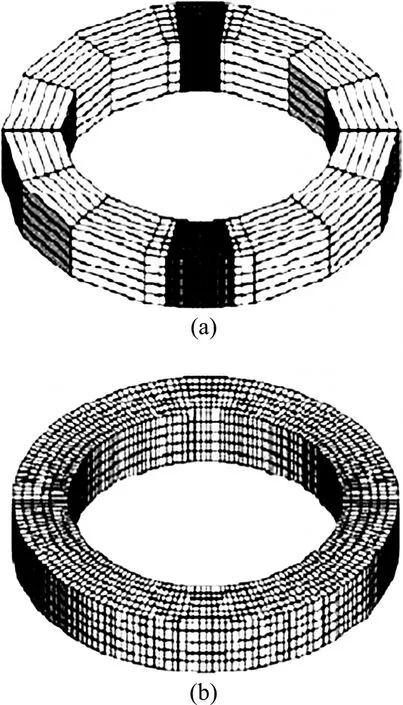
图2 双网格系统组成示意图Fig.2 Schematic diagram of composition of dual-mesh system: (a) Computational mesh; (b) Material mesh

HU等[19]对KIM等[30]所提出的双网格技术进行了改进。主要改进之处在于使计算网格和材料网格在节点处重合，也就是使计算网格成为材料网格的子集，这样变形区内的计算网格和材料网格由于一一对应而不需要在传递变量值时进行插值运算，从而减少了插值误差和插值运算时间，提高了计算效率和精度。他们采用该改进的双网格技术和弹塑性有限元法研究了环件热辗扩成形过程中的金属流动、应变分布和力能参数等。LIM 等[21]运用该改进的双网格技术对Ti-6Al-4V钛合金矩形和V形环热辗扩成形过程进行了热力耦合三维有限元模拟，分析了环件的宽展、应变和温度分布特征。YEA等[31]采用基于双网格技术的刚塑性有限元法预测了矩形和T型碲铅环在热辗扩成形过程中的宽展变化。

MOON等[32]基于HU等[19]的双网格技术，提出一种新的节点更新策略以减小环件的体积改变，在此基础上采用三维刚粘塑性有限元法研究了轴承钢环在热辗扩成形过程中“多边形”缺陷产生的原因。

HIRT等[33]将类似于双网格技术的多网格(Multi-mesh)技术应用于环件热辗扩成形中。多网格技术与双网格技术的不同之处在于计算网格固定于环件材料上，随环件而运动，而在变形区内始终能保持较细密的网格是通过网格重划分来实现的。

双网格技术和多网格技术通过减小环件单元数而使隐式模型的计算效率得到较大提高，但这是以牺牲计算精度为代价的，因为计算网格和材料网格之间频繁的数据传递会引入误差。

1.1.3 任意拉格朗日－欧拉(Arbitrary Lagrangian-Eulerian，ALE)技术

ALE技术是拉格朗日和欧拉描述的有机结合。该技术允许网格扭曲和材料流动相互独立，因而在变形区内总能保持较细密的网格，减少了单元数量。在对环件辗扩成形过程进行模拟时，由于采用传统的拉格朗日描述需要大量的单元而导致耗时过多，而采用欧拉描述难以准确地捕捉环件的几何变化，HU 和 LIU[28]将 ALE技术应用于环件热辗扩成形过程的二维有限元模拟，但他们将整个环件划分成均匀的网格，故不能充分体现ALE技术的优势。

采用 ALE技术可以直接对网格系统和材料系统中的未知变量进行计算，从而避免了两个系统之间相互传递数据而引入的插值误差，但这必然会增加未知变量的个数。针对该问题，DAVEY和WARD[24,29,34−35]在HU 和LIU[28]研究的基础上，提出了算子分裂法，以消除额外的未知变量，同时结合三维刚粘塑性有限元法和一种新迭代求解算法——连续预置共轭梯度法，实现了异型环件径轴向热辗扩成形过程的数值模拟，进一步提高了计算效率。

尽管ALE技术可以缩短模拟计算时间，但由于环件辗扩成形的非稳态特征，即变形区的几何形状和大小是瞬时变化的，因此，当材料沿环件周向流过变形区内相对细密网格的同时，变形区网格必须随芯辊的进给运动而沿环件的径向产生移动。而这种网格移动会引入未知变量，给求解增加了困难。

尽管以上这些方法和技术的运用使环件热辗扩成形隐式模型的计算效率得到了一定程度的提高，但仍达不到较高要求。LIM等[21]指出，即使运用双网格技术使计算效率提高了约70%，但计算时间仍然较长。DAVEY和 WARD[34]运用其改进的 ALE技术在 400 MHz的PC机上模拟火车轮箍的径轴向热辗扩成形过程，共耗费机时21 d，并指出计算效率低是环件热辗扩成形过程数值仿真应用于工业实际的最大障碍。ALLWOOD等[36]尽管没有采用耗时的网格重划分技术，但在2.6 GHz的PC机上求解一个完整的三维隐式模型仍需要机时8 d，这显然难以满足工程中工艺和过程设计的需求。鉴于此，研究者开始关注另一种有限元方程求解算法——显式算法。

1.2 显式建模仿真

显式算法最初是用来求解高速动力学问题，如冲击、爆炸等瞬态过程。该算法由于不需迭代求解方程而具有处理高度非线性和大型问题的强大功能，后来，又被应用于金属塑性成形过程等准静态问题的求解，并显示出隐式算法无可比拟的优越性。GROCHE等[37]指出，与隐式算法相比，显式算法能将金属塑性成形过程模拟加速22倍。在文献[38]中，分别采用显式和隐式算法对厚板轧制二维问题进行求解后发现，尽管两者给出了相似的计算结果，但显式算法所耗费的机时只有隐式算法机时的1/13。PAUSKAR等[39]分别采用显式和双网格隐式有限元法对异型环件冷辗扩成形过程进行了模拟，对比后发现，当模型的网格密度相同时，前者的计算效率更高。HAREWOOD和MCHUGH[40]采用显式算法和隐式算法对不同加载条件的适应性进行对比后指出，在涉及接触的加载条件下，显式算法比隐式算法更适合。显式算法尽管是条件稳定的，但其处理动态接触等高度非线性、非连续问题的强大能力，对于塑性成形领域的研究者具有相当大的吸引力。因此，已有不少学者将显式算法应用于环件热辗扩成形过程的建模仿真中。

XIE等[23]针对环件热辗扩开发了三维刚粘塑性有限元显式代码 H-RING，利用该代码研究了矩形环件热辗扩成形过程中“鱼尾”缺陷产生的原因和控制方法，分析了L型环件热辗扩成形过程中的应变分布特征。该代码假设环件每转的变形是稳态的，并且变形区内环件的每个截面均具有完全相同的变形条件；采用不均匀的网格划分方式，即变形区内网格较细密，变形区外网格较稀疏，当环件的几何更新后，运用网格重划分技术使较细密的网格始终位于变形区内。WANG等[22,41−42]采用动力显式软件LS-DYNA实现了碳钢和钛合金异型截面大环热辗扩虚拟成形过程，获得了成形环件的应力、应变和位移分布。兰箭等[43−44]运用ABAQUS/Explicit软件，采用弹塑性显式有限元法模拟了内台阶锥形铅环热辗扩成形过程，对毛坯尺寸和孔型进行了优化。钱东升等[45]运用ABAQUS/Explicit软件建立了铅环热辗扩成形过程三维弹塑性有限元显式模型，并给出了环件热辗扩成形过程建模中质量放大技术的运用原则。

但是，上述研究均是在等温条件下进行的，没有考虑更符合实际的热力耦合效应。XU等[11]通过对比环件热辗扩成形过程的等温和热力耦合模拟结果后指出，相对等温模拟，热力耦合模拟能更准确地预测环件的热力学参数分布，从而可以更可靠地预测和控制环件的微观组织和性能。一些学者采用热力耦合显式有限元法对环件热辗扩成形过程进行了建模仿真。如WANG等[46]通过解决算法中确定热力边界条件和轧辊运动控制等关键技术问题，建立了钛合金大型矩形环件热辗扩成形过程热力耦合三维有限元显式模型(见图3)。潘利波[47]在ABAQUS/Explicit软件平台上，利用热弹塑性材料模型和热力耦合显式有限元法，模拟了铝合金大型矩形环件的径、轴向热辗扩成形过程，获得了成形环件的应力和温度分布以及特征点的温度演变情况。万自永[48]运用LS-DYNA软件，忽略导向辊，建立了GH4169高温合金环径、轴向热辗扩成形过程热力耦合三维弹塑性有限元显式模型，并指出，采用弹塑性显式算法可比采用刚塑性隐式算法的计算效率提高40%左右。GUO和YANG[49]采用与LI等[27]相似的基于液压调节的导向辊运动自适应柔性控制方法，在ABAQUS/Explicit平台上钛合金矩形环件径、轴向热辗扩成形过程热力耦合三维有限元显式模型进行修止，分析了成形环件的尺寸变化与应力、应变和温度的分布特征。

图3 大型环件热辗扩成形热力耦合三维有限元显式模型[46]Fig.3 Coupled thermo-mechanical explicit 3D-FEM model of hot rolling of large ring[46]

显式算法显著提高了环件热辗扩成形过程有限元仿真的计算效率，但随着环件尺寸的增大、形状的复杂化以及对模拟仿真的完善性和自适应性要求的提高，显式算法也面临着如何进一步提高计算效率的问题。

综上所述，环件热辗扩成形宏观有限元建模仿真呈现如下的发展趋势：求解算法在从隐式向显式转化，环件的尺寸在不断扩大，环件的截面形状在不断复杂化，环件材料在从碳钢向难变形材料扩展，环件成形方式在从纯径向辗扩向径轴向辗扩拓展。目前，有关环件径轴向热辗扩，尤其是难变形材料大型复杂环件径、轴向热辗扩成形过程有限元建模仿真的研究鲜有报道。

2 环件热辗扩成形微观组织有限元建模仿真

环件热辗扩成形过程中，在动态、静态回复与再结晶及晶粒长大等多机制综合作用下环件微观组织不断发生变化，最终的组织形态决定了产品的性能。采用实验方法难以对这一复杂过程进行动态观察，凭经验或理论解析也很难进行有效预测和控制，而有限元建模仿真可以弥补上述方法的不足，已成为研究材料成形过程中组织演变的有效途径[50]。

XU和GAO[51]将碳钢组织演变模型嵌入热力耦合刚塑性有限元模拟程序中，对碳钢环热辗扩成形过程组织演变进行模拟，得到了径向变形区外7个横截面上的奥氏体晶粒尺寸及分布。结果表明，通过合理控制速度、温度和冷却条件，在连续多道次轧制作用下，环件的初始晶粒尺寸可以得到细化。该程序假定径向变形区是稳态的，这与实际不符，而且利用该程序只能获得环件上特定截面处的组织特征参数。

欧新哲[52]利用 DEFORM−3D 内置组织模块预测了 40Cr钢环热辗扩成形过程中动态再结晶晶粒尺寸和动态再结晶体积分数等微观特征参量的演变，揭示了工艺参数对组织的影响规律。该组织模块在DEFORM−3D平台上以“后处理程序”模式运行，因此，每次模拟只能获得特定时刻的组织状态，而且难以考虑组织与热力学参数之间的相互影响。

王敏等[53]基于 ABAQUS/ Explicit 软件平台, 采用弹性预估−塑性校正策略和隐式本构积分算法, 将Ti-6Al-4V 钛合金的组织演变模型及与速率相关、温度相关的弹塑性本构模型写入子程序VUMAT , 实现了组织演变与宏观热力学行为的耦合模拟。将该子程序应用于钛合金大型矩形环件热辗扩过程热力耦合三维有限元模拟中, 研究了组织演变的特征与规律，图4所示为β相晶粒尺寸的演变情况。该研究中组织模型来自于 HU等[54]依据热模拟压缩试验建立的经验模型。根据环件热辗扩成形特点，设计并开展相应的物理模拟试验，建立更符合实际的组织模型，以进一步提高组织模拟精度。

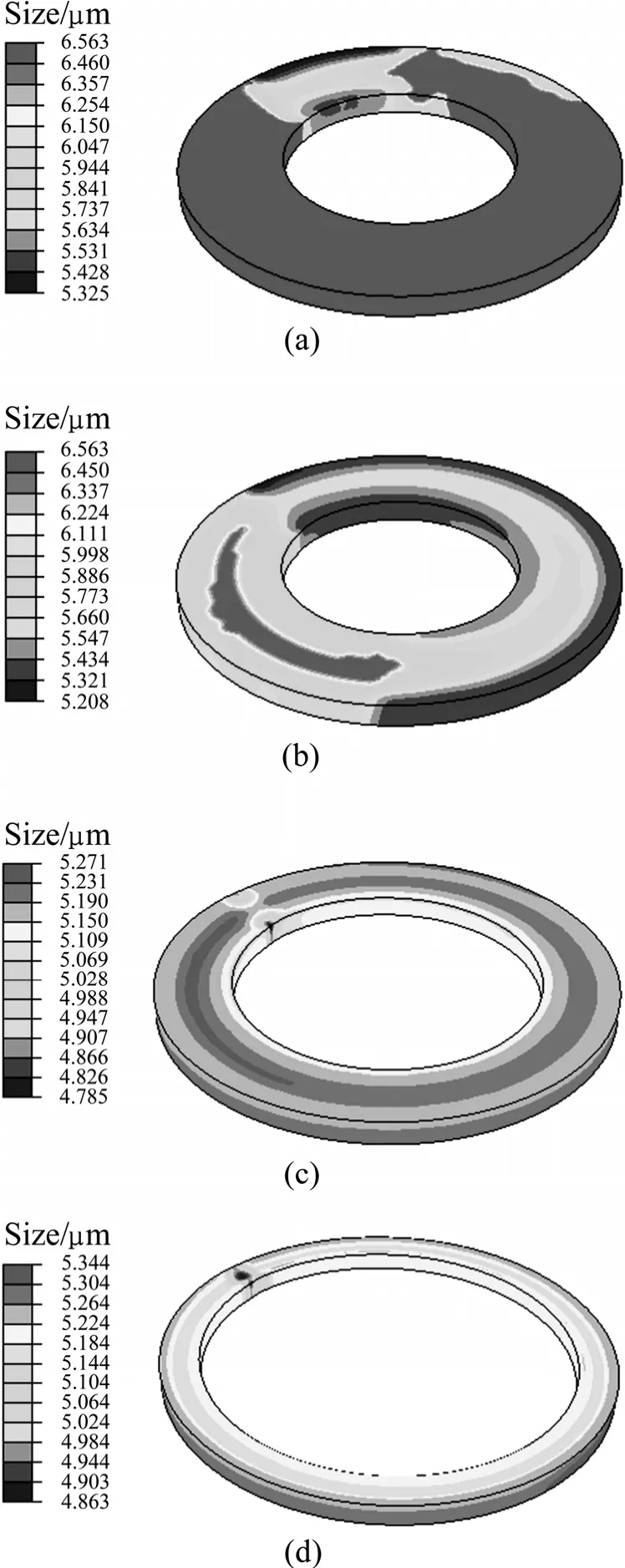
图4 β相晶粒尺寸的演变Fig.4 Grain size evolution of β phase: (a) t=0.8 s; (b) t=1.6 s;(a) t=9.6 s; (a) t=20 s

由上述研究现状可知，目前对环件热辗扩成形微观组织演变有限元建模仿真有待开展更精确、更深入的研究，尤其对大型复杂环件径、轴向热辗扩成形更是如此。

3 结论与展望

1) 有限元建模仿真可以满足对环件热辗扩成形过程的精确、高效和全方位研究以及数字化、高技术化发展的需求，已成为高质量、低成本、短周期、自主创新地实现无缝环形构件开发的强有力工具。分别从宏观和微观尺度评述了环件热辗扩成形有限元建模仿真的国内外研究现状、存在的问题与发展趋势，进而提出其重点发展方向。

2) 需进一步研究和发展大型复杂环件径、轴双向热辗扩成形全过程自适应建模仿真方法与关键技术，如发展可靠、高效、移植性好的轧辊运动自适应柔性控制方法。

3) 将环件热辗扩成形过程宏观和微观有限元建模仿真技术无缝集成，为研究与开发环件宏观和微观成形质量一体化调控技术提供重要手段。

4) 建立适用于环件热辗扩成形的本构模型和组织演变模型，开发稳健、高效的有限元算法、本构积分算法与组织演变仿真方法，为以环件热辗扩为代表的具有复杂动态接触边界条件的连续、局部塑性成形过程宏观和微观建模仿真提供有效途径。

5) 将模具的变形、传热、热疲劳破裂及热磨损等主要失效形式引入环件热辗扩成形过程有限元建模仿真中，为实现成形过程和模具的优化设计与精确控制奠定基础。

6) 面向航空航天、风电、核电、交通等高技术领域的基于全过程建模仿真的难变形材料高性能大型、复杂环件热辗扩成形核心技术，是未来研究发展的重要方向，也是航空航天等重要领域的国家重大战略工程的迫切需求。

REFERENCES

[1] 华 林, 黄兴高, 朱春东. 环件轧制理论和技术[M]. 北京: 机械工业出版社, 2001: 1−5.HUA Lin, HUANG Xin-gao, ZHU Chun-dong. Theory and technology of ring rolling[M]. Beijing: China Machine Press,2001: 1−5.

[2] 杨 合, 孙志超, 詹 梅, 郭良刚, 刘郁丽, 李宏伟, 李 恒, 吴跃江. 局部加载控制不均匀变形与精确塑性成形研究进展[J].塑性工程学报, 2008, 15(2): 6−13.YANG He, SUN Zhi-chao, ZHAN Mei, GUO Liang-gang, LIU Yu-li, LI Hong-wei, LI Heng, WU Yue-jiang. Advances in control of unequal deformation by locally loading and theories related to precision plastic forming[J]. Journal of Plasticity Engineering, 2008, 15(2): 6−13.

[3] GROCHE P, FRITSCHE D, TEKKAYA E A. Incremental bulk metal forming[J]. Annals of the CIRP, 2007, 56: 635−656.

[4] YANG H, ZHAN M, LIU Y. Some advanced plastic processing technologies and their numerical simulation[J]. Journal of Materials Processing Technology, 2004, 151: 63−69.

[5] 刘建生, 陈慧琴, 郭晓霞. 金属塑性加工有限元模拟技术与应用[M]. 北京: 冶金工业出版社, 2003: 10−25.LIU Jian-sheng, CHEN Hui-jin, GUO Xiao-xia. Finite element simulation technique and application of metal plastic forming[M]. Beijing: Metallurgical Industry Press, 2003: 10−25.

[6] YANG D Y, KIM K H. Rigid-plastic finite element analysis of plain strain ring rolling[J]. International Journal of Mechanical Sciences, 1988, 30: 571−580.

[7] SONG J L, DOWSONA A L, JACOBSA M H, BROOKS J,BEDEN I. Coupled thermo-mechanical finite-element modeling of hot ring rolling process[J]. Journal of Materials Processing Technology, 2002, 121: 332−340.

[8] TSZENG T C, ALTAN T. Investigation of ring rolling by pseudo plane strain FEM analysis[J]. Journal of Material Processing Technology, 1991, 27: 151−161.

[9] WARD M J, MILLER B C, DAVEY K. Simulation of a multi-stage railway wheel and tyre forming process[J]. Journal of Materials Processing Technology, 1998, 80/81: 206−212.

[10] JOUN M S, CHUNG J H, SHIVPURI R. An axisymmetric forging approach to perform design in ring rolling using a rigid-viscoplastic finite element method[J]. International Journal of Machine Tools and Manufacture, 1998, 38: 1183−1191.

[11] XU S G, WEINMAM K J, YANG D Y. Simulation of the hot ring rolling process by using a thermo-coupled three-dimensional rigid-viscoplastic finite element method[J]. Journal of Manufacture Science and Engineering, 1997, 119: 542−549.

[12] XU S G, LIAN J C, HAWKYARD J B. Simulation of ring rolling using a rigid-plastic finite element model[J]. International Journal of Mechanical Sciences, 1991, 33(5): 393−401.

[13] 许思广, 曹起骧, 连家创. 异形截面环件轧制过程的三维有限元分析[J]. 锻压机械, 1994(3): 8−11.XU Si-guang, CAO Qi-xiang, LIAN Jia-chuang. Three dimensional finite element analysis of profiled ring rolling[J].Metal Forming Machinery, 1994(3): 8−11.

[14] 许思广, 曹起骧, 连家创, 姚开云，郭希学. 环件轧制的热刚塑性耦合有限元分析[J]. 机械工程学报, 1994, 30(2): 87−92.XU Si-guang, CAO Qi-xiang, LIAN Jia-chuang, YAO Kai-yun,GUO Xi-xue. Coupled thermal and rigid-plastic finite element analysis of ring rolling[J]. Chinese Journal of Mechanical Engineering, 1994, 30(2): 87−92.

[15] 许思广, 曹起骧, 连家创. 环件轧制中的温度分析[J]. 锻压技术, 1993(6): 34−38.XU Si-guang, CAO Qi-xiang, LIAN Jia-chuang. Temperature analysis of ring rolling[J]. Forging and Stamping Technology,1993(6): 34−38.

[16] YANG D Y, KIM K H, HAWKYARD J B. Simulation of T-section profile ring rolling by the 3-D rigid-plastic finite element method[J]. International Journal of Mechanical Sciences,1991, 33(7): 541−550.

[17] KIM K H, SUKH G, HUBM Y. Development of the profile ring rolling process for large slewing rings of alloy steels[J]. Journal of Materials Processing Technology, 2007, 187/188: 730−733.

[18] MAMALIS A G, JOHNSON W, HAWKYARD J B. Pressure distribution, roll force and torque in cold ring rolling[J]. Journal of Mechanical Engineering and Science, 1976, 18(4): 196−209.

[19] HU Z M, PILLINGER I, HARTLEY P. Three-dimensional finite-element modelling of ring rolling[J]. Journal of Materials Processing Technology, 1994, 45: 143−148.

[20] GUO L G, YANG H, ZHAN M. Simulation for guide roll in 3D-FE analysis of cold ring-rolling[J]. Material Science Forum,2004, 471/472: 760−764.

[21] LIM T, PILLINGER I, HARTLEY P. A finite-element simulation of profile ring rolling using a hybrid mesh model[J]. Journal of Materials Processing Technology, 1998, 80/81: 99−205.

[22] WANG Z W, ZENG S Q, YANG X H, CHENG C. The key technology and realization of virtual ring rolling[J]. Journal of Materials Processing Technology, 2007, 182: 374−381.

[23] XIE C L, DONG X H, LI S J, HUANG S H. Rigid–viscoplastic dynamic explicit FEA of the ring rolling process[J]. International Journal of Machine Tools and Manufacture, 2000, 40: 81−93.

[24] DAVEY K, WARD M J. An efficient solution method for finite element ring-rolling simulation[J]. International Journal for Numerical Methods in Engineering, 2000, 47(12): 1997−2018.

[25] FOROUZAN M R, SALIMI M, GADALA M S, ALJAWI A A.Guide roll simulation in FE analysis of ring rolling[J]. Journal of Materials Processing Technology, 2003, 142: 213−223.

[26] FOROUZAN M R, SALIMI M, GADALA M S.Three-dimensional FE analysis of ring rolling by employing thermal spokes method[J]. International Journal of Mechanical Sciences, 2003, 45: 1975−1998.

[27] LI L, YANG H, GUO L, SUN Z. A control method of guide rolls in 3D-FE simulation of ring rolling[J]. Journal of Materials Processing Technology, 2008, 205: 99−110.

[28] HU Y K, LIU W K. ALE finite element formulation for ring rolling analysis[J]. International Journal of Numerical Methods in Engineering, 1992, 33: 1217−1237.

[29] DAVEY K, WARD M J. A practical method for finite element ring rolling simulation using ALE flow formulation[J].International Journal of Mechanical Sciences, 2002, 44:165−190.

[30] KIM N, MACHIDA S, KOBAYASHI S. Ring rolling process simulation by the three dimensional finite element method[J].International Journal of Machine Tools and Manufacture, 1990,30: 569−577.

[31] YEA Y, KO Y, KIMA N, LEE J. Prediction of spread, pressure distribution and roll force in ring rolling process using rigid-plastic finite element method[J]. Journal of Materials Processing Technology, 2003, 140: 478−486.

[32] MOON H K, LEE M C, JOUN M S. Predicting polygonal-shaped defects during hot ring rolling using a rigid-viscoplastic finite element method[J]. International Journal of Mechanical Sciences, 2008, 50: 306−314.

[33] HIRT G, KOPP R, HOFMANN O, FRANZKE M, BARTON G.Implementing a high accuracy multi-mesh method for incremental bulk metal forming[J]. Annals of the CIRP, 2007, 56:313−316.

[34] DAVEY K, WARD M J. An ALE approach for finite element ring-rolling simulation of profiled rings[J]. Journal of Materials Processing Technology, 2003, 139: 559−566.

[35] DAVEY K, WARD M J. The practicalities of ring rolling simulation for profiled rings[J]. Journal of Materials Processing Technology, 2002, 125: 619−625.

[36] ALLWOOD J M, KOPP R, MICHELS D, MUSIC O, ÖZTOP M,STANISTREET T F, TEKKAYA A E, TIEDEMMAN I. The technical and commercial potential of an incremental ring rolling process[J]. CIRP Annals: Manufacturing Technology, 2005, 54:233−236.

[37] GROCHE P, FRITSCHE D, TEKKAYA E A, ALLWOOD J M,HIRT G, NEUGEBAUER R. Incremental bulk metal forming[J].CIRP Annals: Manufacturing Technology, 2007, 56: 635−656.

[38] ABAQUS Inc. ABAQUS example problems manual[EB/OL].[2003-02-02]. http://wm: 2080/v6.4/books/exa/default. htm.

[39] PAUSKAR P M, SAWAMIPHAKDI K, JIN D Q. Static implicit vs dynamic explicit finite element analysis for ring rolling process modeling[C]//NUMIFORM 2004. Ohio, 412−417.

[40] HAREWOOD F J, MCHUGH P E. Comparison of the implicit and explicit finite element methods using crystal plasticity[J].Comp Mater Sci, 2007, 39: 481−494.

[41] 王泽武. 航空发动机环形锻件成形制造过程有限元仿真[J].航空制造技术, 2009, 20: 68−71.WANG Ze-wu. Finite element simulation on the deforming process of aero-engine annular blanks[J]. Aviation Manufacturing Technology, 2009, 20: 68−71.

[42] 袁海伦, 王泽武, 曾 青, 王 乘. 异形截面环件虚拟轧制及其工艺优化[J]. 塑性工程学报, 2006, 13(6): 15−18.YUAN Hai-lun, WANG Ze-wu, ZENG Qing, WANG Cheng.Virtual ring rolling and the process optimization of profile ring[J]. Journal of Plasticity Engineering, 2006, 13(6): 15−18.

[43] 兰 箭, 左治江, 韩星会, 赵玉民，华 林. 内台阶锥形环件辗扩锻件设计方法研究[J]. 塑性工程学报, 2006, 13(2): 51−55.LAN Jian, ZUO Zhi-jiang, HAN Xing-hui, ZHAO Yu-min, HUA Lin. Research on design method of conical ring with inner steps for rolling process[J]. Journal of Plasticity Engineering, 2006,13(2): 51−55.

[44] 韩星会, 华 林, 兰 箭, 左治江. 内台阶锥形环件轧制三维有限元模拟和工艺优化设计[J]. 中国机械工程, 2007, 18(16):1979−1983.HAN Xing-hui, HUA Lin, LAN Jian, ZUO Zhi-jiang.Three-dimensional finite element simulation and optimal design of ring rolling of conical ring with inner steps[J]. Chinese Mechanical Engineering, 2007, 18(16): 1979−1983.

[45] 钱东升, 华 林, 左治江, 袁银良. 环件轧制三维有限元模拟中质量缩放方法的应用[J]. 塑性工程学报, 2005, 12(5): 86−91.QIAN Dong-sheng, HUA Lin, ZUO Zhi-jiang, YUAN Yin-liang.Application of mass scaling in simulation of ring rolling by three-dimensional finite element method[J]. Journal of Plasticity Engineering, 2005, 12(5): 86−91.

[46] WANG M, YANG H, SUN Z C, GUO L G. Dynamic explicit FE modeling of hot ring rolling process[J]. Transactions of Nonferrous Metals Society of China, 2006, 16(6): 1274−1280.

[47] 潘利波. 环件径轴向轧制变形规律与 CAPP系统研究[D]. 武汉: 武汉理工大学, 2007: 65−90.PAN Li-bo. On deformation laws and CAPP system for radial-axial ring rolling[D]. Wuhan: Wuhan University of Technology, 2007: 65−90.

[48] 万自永. 难变形材料环件轧制过程的三维有限元数值模拟[D].西安: 西北工业大学, 2007: 41−58.WAN Zi-yong. Three-dimensional finite element simulation of ring rolling for difficult-to-deformation material[D]. Xi’an:Northwestern Polytechnical University, 2007: 41−58.

[49] GUO L G, YANG H. Key technologies for 3D-FEM modeling of radial-axial ring rolling process[J]. Materials Science Forum,2008, 575/578: 367−372.

[50] SCHIKORRA M, DONATI L, TOMESANI L. Microstructure analysis of aluminum extrusion: Prediction of microstructure on AA6060 alloys[J]. Journal of Materials Processing Technology,2008, 201: 156−162.

[51] XU S G, CAO Q X. Numerical simulation of the microstructure in the ring rolling of hot steel[J]. Journal of Material Processing Technology, 1994, 43: 221−235.

[52] 欧新哲. 金属环件热辗扩宏微观变形三维热力耦合有限元分析[D]. 西安: 西北工业大学, 2007: 35−50.OU Xin-zhe. Coupled thermo-mechanical 3D-FEM simulation of macro-micro-scale deformation during metal hot ring rolling[D]. Xi’an: Northwestern Polytechnical University, 2007:35−50.

[53] 王 敏, 杨 合, 郭良刚, 孙志超. 基于3D-FEM的大型钛环热辗扩成形微观组织演变仿真[J]. 塑性工程学报, 2008, 15(6):76−80.WANG Min, YANG He, GUO Liang-gang, SUN Zhi-chao.Simulation of microstructure evolution during hot rolling of large rings of titanium alloy based on 3D-FEM[J]. Journal of Plasticity Engineering, 2008, 15(6): 76−80.

[54] HU Z M, BROOKS J W, DEAN T A. Experimental and theoretical analysis of deformation and microstructural evolution in the hot-die forging of titanium alloy aerofoil sections[J].Journal of Materials Processing Technology, 1999, 88: 251−265.

Research development of finite element modeling and simulation of hot ring rolling

WANG Min1,2, YANG He2, GUO Liang-gang2
(1. Department of Materials Science and Engineering,Hubei University of Automotive Technology, Shiyan 442002, China;2. State Key Laboratory of Solidification Processing, School of Materials Science and Engineering,Northwestern Polytechnical University, Xi’an 710072, China)

Hot ring rolling is a highly nonlinear problem under coupled effects of multi-fields and multi-factors, which is characterized by three-dimensional incremental deformation, unsteady state and asymmetry. The research and development of the technology using finite element (FE) modeling and simulation is of significance for manufacturing seamless ring-shaped components with high quality, low cost and short cycle. The current international level, remained problems and development trend of macro-scale and micro-scale FE modeling and simulation of hot ring rolling were reviewed, and the following prospects of important directions were presented as follows: adaptive modeling method and key technologies for the overall process of hot radial-axial rolling of large profiled rings; seamless integration of macro-scale and micro-scale FE modeling for hot ring rolling; the processes such as ring rolling, and relevant FE algorithm, constitutive integration algorithm and microstructure evolution simulation method; hot ring rolling simulation accounting for deformation, heat transfer and major failure modes of dies.

hot ring rolling; microstructure; modeling; simulation; finite element

TG335.19

A

1004-0609(2011)07-1647-09

国家自然科学基金重点项目(50935007)；国家自然科学基金面上项目(50805120)；国家重大科技专项(2009ZX04014-074-03)

2010-04-12；

2010-12-21

王 敏，博士；电话：0719-8238783；E-mail：sprit418@mail.nwpu.edu.cn

(编辑 陈卫萍)