新建正激变换器运行理论

2011-11-24孙定浩叶东东

空间控制技术与应用 2011年3期

关键词：磁芯等效电路磁化

孙定浩，张扬，叶东东

(北京控制工程研究所，北京100190)

将上式以及V=2E代入式(11)得P2′的纵坐标

新建正激变换器运行理论

孙定浩，张扬，叶东东

(北京控制工程研究所，北京100190)

用两种与传统不同的电路模型表征正激变换器.其一用LC串联谐振实现磁复位功能(这一模型中没有磁复位绕组，并确认开关管存在与其并联的电容).其二主要用磁复位绕组实现磁复位功能(这一模型中有磁复位绕组，但也确认开关管存在与其并联的电容).用相平面分析法分析这些模型，得到了正激变换器运行时电路和磁路特征参量的解析表达式.本文的分析和解析结果以及后续对这两种正激变换器的全面分析被称为“新建正激变换器运行理论”.

正激变换器；相平面分析；电路

正激变换器是直流变换器中最早出现的电路拓扑之一，其运行理论广见于直流变换器专著[1-4]中.就我们所见，其所用的电路模型均作了两个重要假设：

1)忽略开关管旁路电容，即不考虑开关管寄生电容以及各种缓冲、钳位电路在开关管两端产生的并联等效电容对变换器运行的影响.

2)采用磁芯复位绕组或电压钳位等专门措施实现变压器磁芯复位，即在一个周期结束时使磁芯的B值返回到这个周期开始的B值.

在这两个假设条件下，得到许多结论，其中最重要的是，正激变换器的磁芯是单向磁化的；当磁芯复位绕组匝数与初级绕组匝数相同，正激变换器的占空比必须小于0.5.

我们注意到，在功率MOS(其D-S间寄生电容均几百皮法以上)广泛用来作正激变换器开关管，以及现行正激变换器的运行频率均高达几百千赫兹的情况下，以上假定(1)已不允许；另一方面，这种情况下的正激变换器可以利用开关管断开时变压器初级绕组电感L与开关管并联等效电容C产生的LC串联谐振来实现磁芯复位，于是以上假设(2)失去普遍意义，它只在一些情况下是必要的.因此在以上两个假定下所得的结论只在某些特殊情况下成立，不具普遍性.

本文新建正激变换器运行理论的思路是，首先讨论这种变换器中没有磁芯复位绕组，确认开关管并联等效电容C存在的情况.充分讨论这种利用LC串联谐振实现磁芯复位时电路和磁芯运行的许多特征，其中包括开关管最高运行电压的解析表达式.这个表达式表明了对于一个给定的设计问题是否可以利用LC串联谐振实现磁芯复位以及如何改变参数(包括L、C以及占空比D和运行周期 T)以实现这种可能性.考虑到实际问题的许多限制，尚有无法用这种方法使磁芯复位的情况，我们接着在以上电路拓扑中引入磁芯复位绕组，作为另一种正激变换器电路模型讨论.这样就得到两种模型的解析结果，以此构成新建的正激变换器运行理论.

现基于相平面分析法[5-8]，讨论利用LC串联谐振实现磁芯复位的正激变换器(下称“无磁复位绕组正激变换器”).相平面的纵坐标为变压器初级绕组中等效的磁化电流 im，横坐标为开关 K两端电压，相平面被划分为四个区域.分别讨论开关在“接通(Ton)”和“断开(Toff)”两种状态时，这种正激变换器处于每个区域中任意一点的相迹.然后按Ton→Toff→Ton→…的运行顺序，绘制运行相迹图.得到了这种正激变换器运行时相迹“发散”和“收敛”的条件，稳态运行时相迹环的特征参数与正激变换器基本物理参数之间的关系.接着分析有磁复位绕组的正激变换器的运行过程，并讨论了C→0的 “极限”情况.

E—一次电源输入电压；

Vo—二次电源输出电压；

K—采用PWM集成电路控制的开关；

V—开关K两端电压；

im—变压器初级绕组中“等效”的磁化电流；

im′—im在变压器次级绕组或磁复位绕组中的折合电流；

L—变压器初级绕组电感；

C—与开关K并联的电容；

D1—整流二极管；

D2—续流二极管；

D3—磁复位绕组二极管；

is—流过滤波电感的电流；

is′— is在变压器初级绕组的折合电流；

T—正激变换器运行周期；

D—稳态运行占空比；

Ni—变压器初级绕组匝数；

No—变压器次级绕组匝数；

Nd—变压器去磁绕组匝数.

注：本文所有元器件均采用理想模型.

1 无磁复位绕组正激变换器的等效电路和相迹

图1(a)为开关K导通时的等效电路，此时D1导通，其相迹图如图2(a)所示.设开关K导通起始时，相点在相平面上任意一点 P0(V(0)(0))，它将跳变到状态(0(0))，即经 Δt→0到达 im轴上=(0)处.此后在轴上的运行方程为

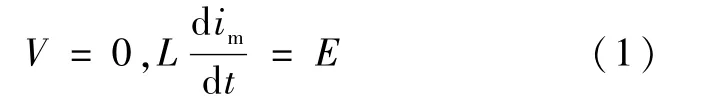
式中，t=0时im=im(0).上式的解为

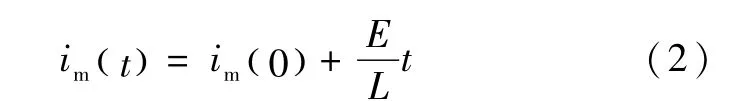
在这个过程中流过变压器初级绕组的电流im和is′经开关K返回一次电源.

图1(b)为开关K断开，相点在 im＞0，0＜V＜E的等效电路，此时D1依然导通.因此im和is′经电容C返回一次电源.设 is′＞＞im(Ton)，则电容 C两端电压V以极快速率上升到一次电源电压E.在实际情况中，这段时间通常可以忽略，故相应的im增量也可忽略.因此，相迹如图2(b)中所示用一组与 V平行的直线近似.

图1(c)为开关 K断开时，相点在 im＞0，V＞E的等效电路，此时 D1断开，D2导通.此时图1(c)中变压器左侧电路等效于一次电源E接 LC串联.

设开关K导通时间长度为Ton，相点在im轴上，由im(0)向上移到

图1 无磁复位绕组正激变换器在所处(V，i m)相平面中不同区域的等效电路

图1(d)为开关K断开时，相点在 im＜0，V＞E的等效电路.此时 D1仍维持断开状态，D2导通.左侧电路仍等效于一次电源E接LC串联，但电流im反向.

图1(e)为开关 K断开时，相点在 im＜0，0≤V＜E的等效电路，此时 D1导通，D2断开.is′和 im经电容C返回一次电源，设 is′＞＞im，则电容 C两端的电压V仍以极快速率上升到E，相应的im增量亦可忽略.其相迹用一组与V轴平行的直线近似，方向指向直线EP4，如图2(b)所示.

图1(f)为开关 K断开时，相点在 im＜0，直线V=E上的等效电路，此时初级绕组感应电压为零.D1和D2均导通，次级绕组此时等效于短路绕组，它将im从初级绕组中转移到次级绕组中，并以此短路状态保持着磁芯的储能.此时初级绕组中实际电流为零，等效磁化电流im保持不变.

现讨论图1(c)、(d)运行的相迹，其动态方程为

将上式改写成

设t=0，相点在图2(b)的直线EF上P2点，即

式(5)的通解为

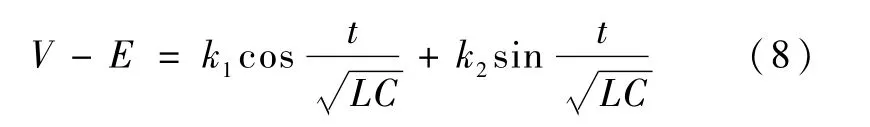
其中k1、k2为待定系数.

将式(6)和(7)代入式(8)可以得到

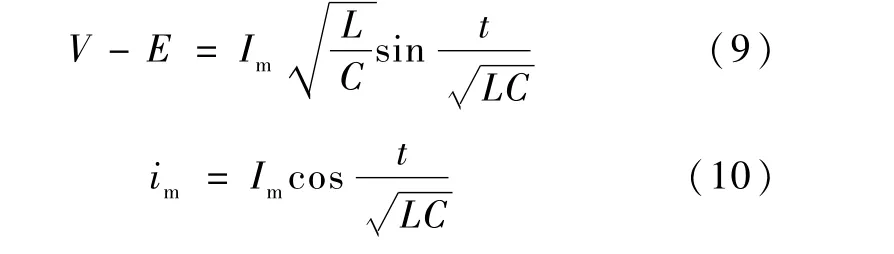
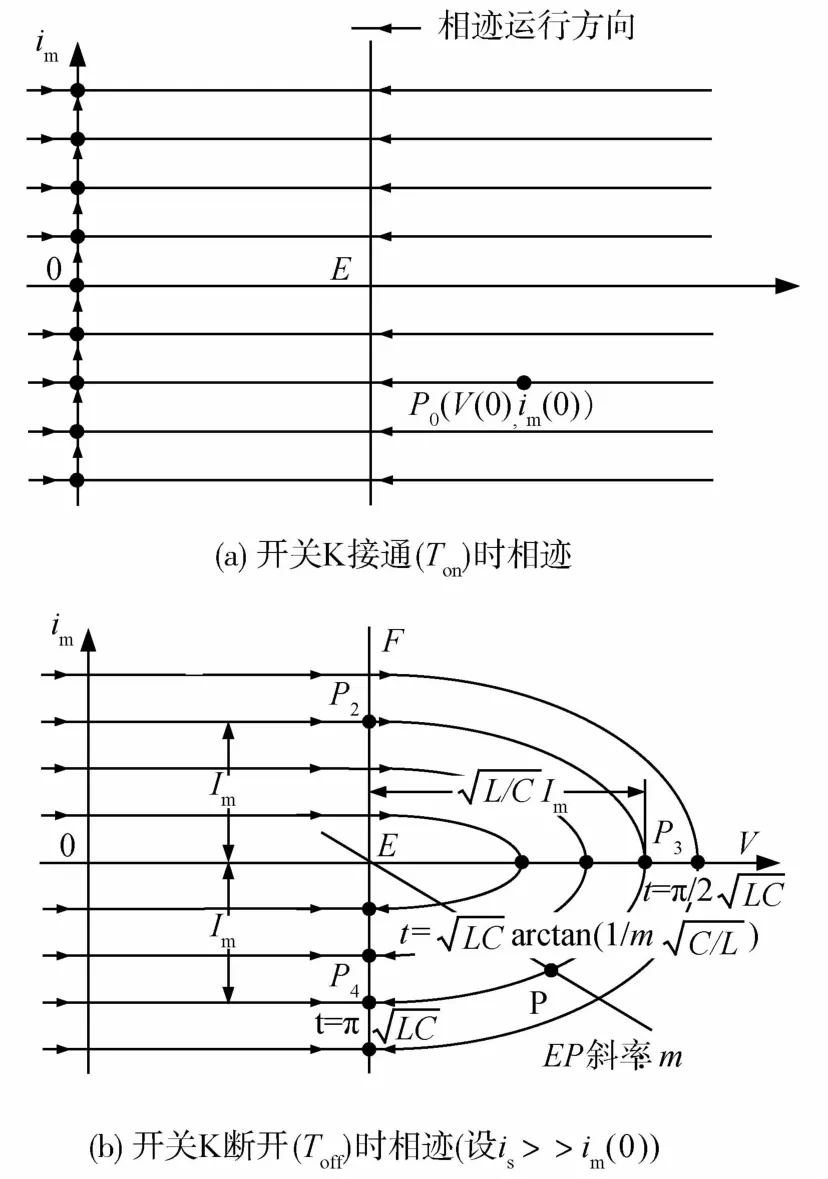
图2 变换器在(V，i m)相平面中的相迹图

由式(9)和(10)可以得到相平面(V，im)中相迹的方程

现求相迹从P2点到达过E点斜率为m的直线EP所经的时间.

直线EP的方程为

将式(9)、(10)代入式(12)得

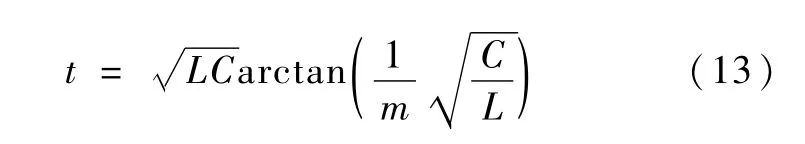
式(13)与Im无关，与 m有关.这即证明从EP2轴上任一点经相同时间到达直线EP上.由式(13)可知，到达直线EP3的时间是 π到达直线EP4的时间是π

2 运行相迹的发散和收敛

设无磁复位绕组正激变换器的运行周期为T，占空比为 D，则 Ton为 DT，相应的 Toff为(1-D)T.

设起点在 P0(0，0)，正激变换器按 Ton→Toff→Ton…顺序运行.现根据图2相迹图绘制正激变换器运行相迹.图3(a)是当 (1-D) T＜π时的运行相迹，此时直线EP斜率 m＞0.相迹从 P0开始经 Ton到达 P1而后 Toff，P1则跳到 P2，再经椭圆线P2P3到达 P3.此时 Toff结束.开关 K重新接通，相迹从P3跳到P4开始第二次Ton.由图可见，这第二周期的起点P4位于前一周期起点P0之上.如此再做运行相迹便知，以后的相迹环将保持在im＞0区域，逐步上升，最后在一个im较高的区域内形成一个稳定的闭环，这个过程我们称为“相迹发散”.在这个过程中，变压器磁芯可能饱和，是设计这类变换器时应该避免发生的情况.时的运行相迹，此时直线 EP斜率 m＜0.相点从 P0开始沿P0P1P2P3运行.下一周期开始跳到P4点，其im值为负.再做运行相迹便知，以后的相迹在im轴方向，上不能高于P1，下不能低于P4.这种im幅值限定在一定范围的过程称为“相迹收敛”.它保证磁芯B值只在一定区域内运行.

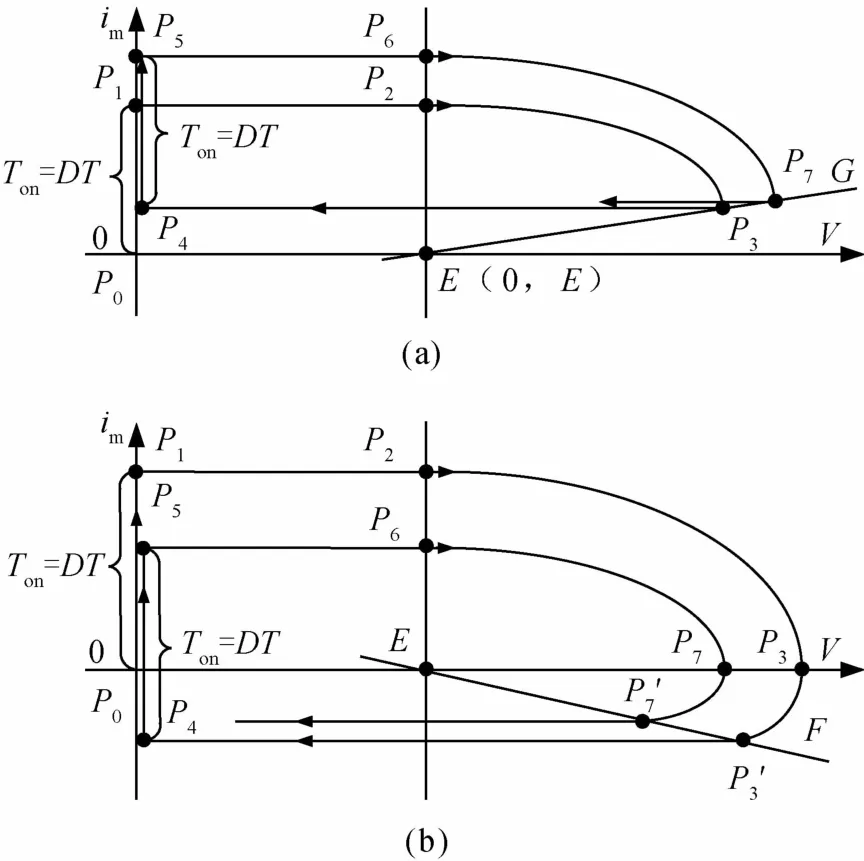
图3 运行相迹的发散(a)和收敛(b)

以上讨论可知，判定正激变换器运行过程相迹收敛的准则是

图3(b)是当

3 稳态相迹环(当π＞(1-D) T＞π)

正激变换器(理想模型)稳态运行时的占空比为

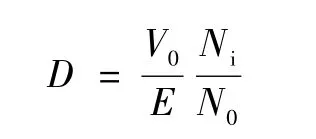
P2和P这两点在纵坐标方向的距离应等于DT过程中纵坐标的增量，由此可建立方程

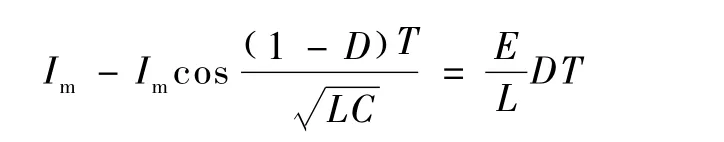
由上式得

将式(16)代入式(15)

将式(16)和 im=0代入式(11)得 P3的 V值，即正激变换器运行的最高电压

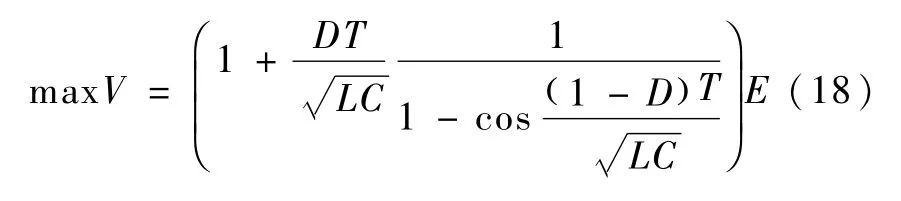
至此，稳态相迹环的特征参数(Im、I和 max V)均由正激变换器基本参数(E、T、D、L和 C)表达.此时 V～t和 im～t的波形如图4(b)、(c)所示.

4 最优稳态相迹环(当(1-D)T＞π)

从图2相迹可知，当时间将到达并停留在P2的对称点P4，由此便知，变压器T的磁芯被“对称磁化”.将这一特征引入公式(3)得

将式(19)和 im=0代入式(11)得 P3的 V值，即此时正激变换器的最高电压

图5(a)示出此时的稳态相迹环.图5(b)为当输入电压E减小为E′时的稳态相迹环，此时正激变换器占空比D相应增大至D′，满足等式EDT=E′D′T.

图4 π(1-D)T＞π/2时稳定运行环(a)和V～t波形(b)

图5(a)的V～t和 im～t波形如图5(c)和(d)所示，波形中出现“平台”.设计者通常希望max V≤2E，由上式可知，当 DT/21时，满足这一要求；当1时，不满足.此时正激变换器应采取其他措施，如变压器中增设磁复位绕组等.

现在我们讨论电源电压可在 E～E/2之间变化，限定max V≤2E时，如何确定 E/2时的占空比.设电源电压为E时，取令正激变换器运行在对称磁化工况.当电源电压为E/2时，正激变换器为保证输出电压V0稳定，；令变换器仍处于对称磁化工况，则应满足条件 T-取，故E/2时的占空比：

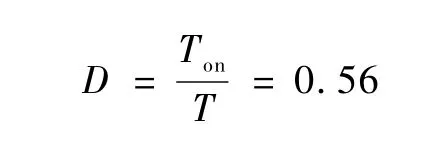
满足maxV≤2E.可以证明，满足这一条件的最短周期近似为，此时占空比为0.67.

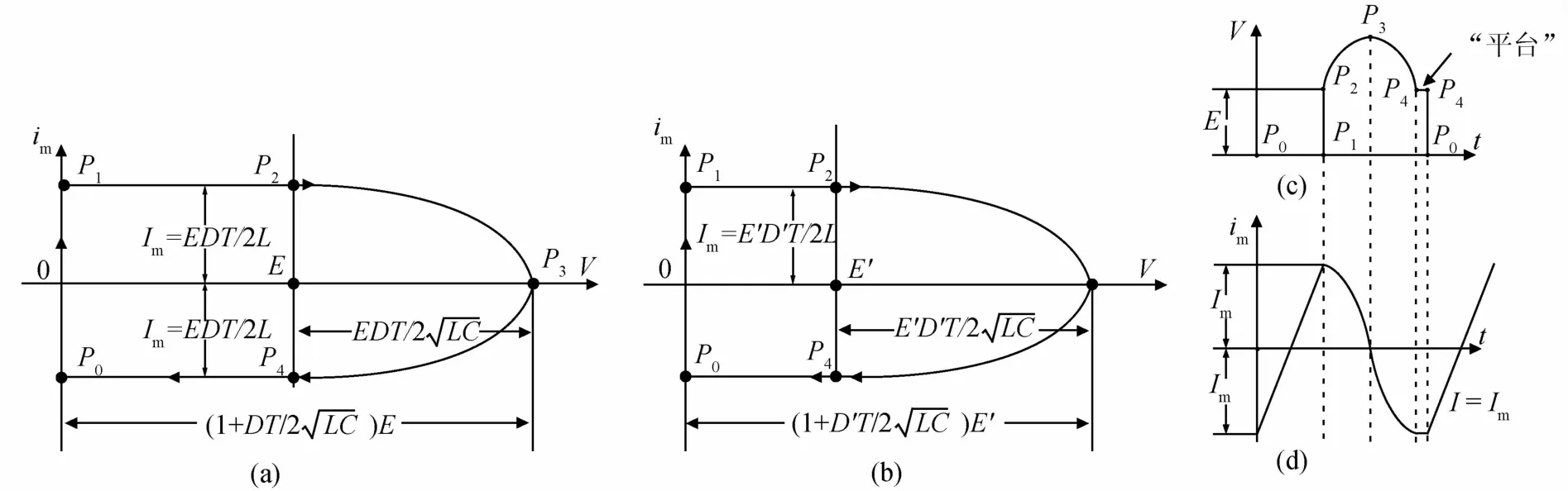
图5 (1-D)T＞π时稳定运行环(a)和V～t波形(b)

现说明出现图5(c)所示“平台”时正激变换器运行的优点.在一个周期内，即图5中从 P0开始再返回到P0止，唯有P4到P0是能量消耗过程：电容C在P4点的能量CE2/2在开关K接通时消耗在开关K中.由图2可知，P4点是LC串联谐振“去磁”能达到的最低点(V=E)，因此“平台”的出现标志着当前电容功耗最低.另一方面，当 “平台”出现则表明磁芯被对称磁化，磁通密度的幅值最低，磁芯运行损失最小.

5 有磁复位绕组时等效电路和相迹

图6示出有磁复位绕组的正激变换器，当Nd=Ni，能实现 max V=2E.

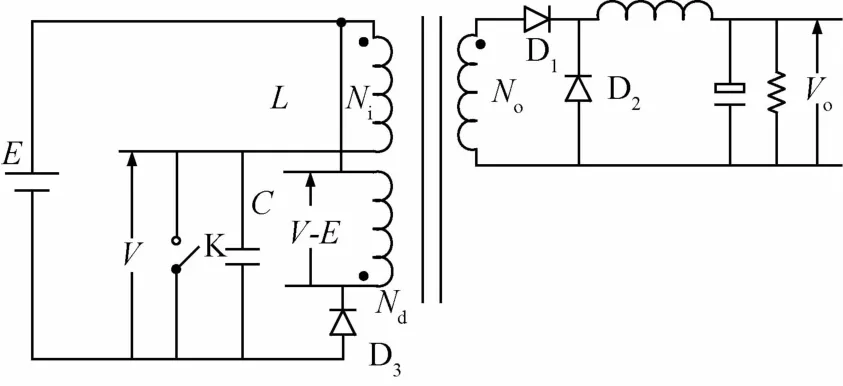
图6 有磁复位绕组的正激变换器

其中，im(0)是当V=2E的起始时刻im的值.

由于磁复位绕组不能穿过im＜0的电流，也不能在V＜2E时流过im＞0的电流，因此，在不是V=2E，im＞0的情况，变换器的运行过程与LC串联谐

图7示出这种变换器在 Toff状态，V=2E时，初级绕组磁化电流im改由磁复位绕组通过的情况：此时D1断，D2和D3通，im转移到磁复位绕组，按下列方程下降为零：振磁复位情况完全一样.由此得图8所示的相迹图.

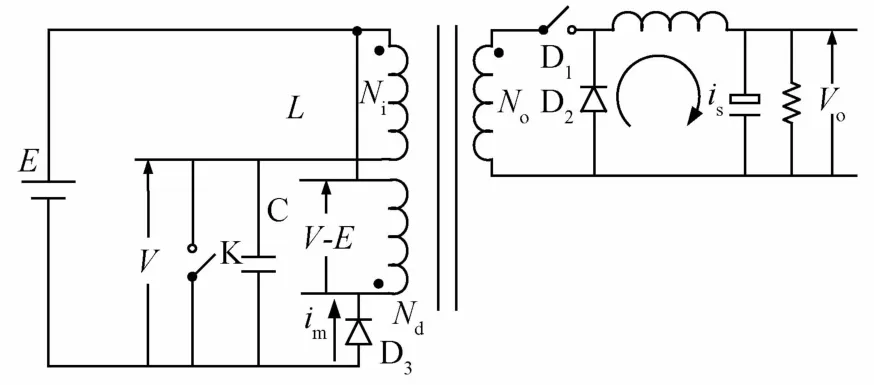
图7 当 V=2E，i m＞0时图6的等效电路

根据图2(a)和图8(a)，图8(b)构造了一类通常发生的稳态运行的相迹环.

将V=2E，im=0代入式(11)所得的Im即P4点的纵坐标

这是有磁复位绕组时的一个重要特征：反向磁化电流的I值与占空比D和T无关.将式(22)的 I作为im(0)代入式(3)的im(Ton)，即图9中的Im由上式得直线EP2′的斜率

将上式以及V=2E代入式(11)得P2′的纵坐标

将式(25)的 m值代入式(13)得 P2P2′经历的时间.式(24)代入(21)得 P2′P3经历的时间.P3P4经历时间是 π/2.容易证明，从 P2到 P3的时间大于π/2.因此要实现图9所示的相迹环，所需的Toff时间比图5所示相迹环更长一些.至此，相迹环上各点的坐标及其间经历的时间均由正激变换器的基本物理变参数(E、T、D、L和C)表达，相平面分析的基本部分完成.

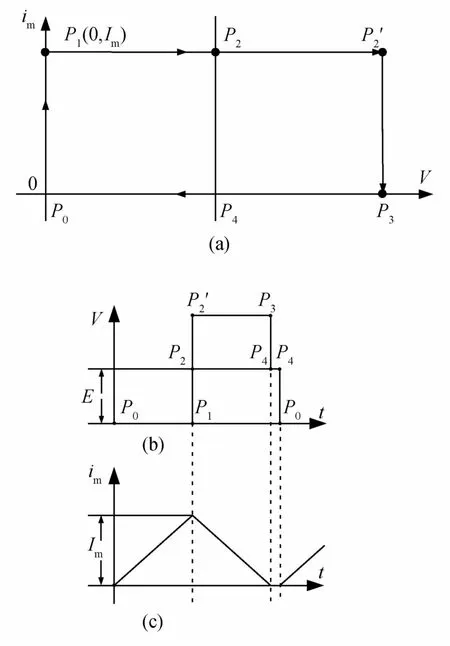
图9 C→0时的相迹环

6 有磁复位绕组时的极限情况

由式(22)可见，当 C→0，则 I→0.由式(23)Im=DTE/L.这时图8演变为图9，im≥0，磁芯被“单向磁化”.因此许多文献所述的“正激变换器磁芯是单向磁化”，并认定这是正激变换器的一大缺点的观点，只在C→0时或＜π/2时是正确的.

7 最优稳态相迹环试验

我们实际开发了用LC串联谐振实现磁复位的正激变换器，利用其电路拓扑简单，可实现对称磁化的特点.具体参数如下：变压器初级绕组电感约为165μH，并联电容约为1600pF，正激变换器运行周期约为3.3μs，稳态运行占空比约为40%，电源电压26.4V.将以上数值代入式(20)得与图10所示的实测结果一致.

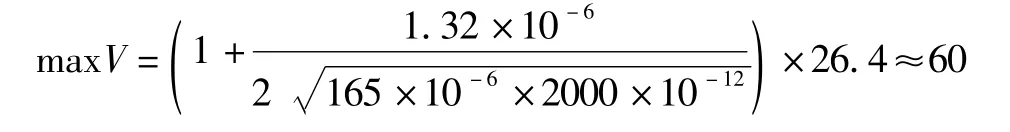
图10 正激变换器开关两端电压的实测波形

8 结束语

作者将根据本文所得的基本结果，在后续的文章中对无磁复位绕组和有磁复位绕组的正激变换器进行全面分析，以充实这一运行理论.

[1] 蔡宣三，龚绍文.高频功率电子学[M].北京：科学出版社，1993[2] 张占松，蔡宣三.开关电源的原理与设计[M].北京：电子工业出版社，2000

[3] McLyman CW T.变压器与电感器设计手册[M].北京：中国电力工业出版社，2004

[4] Lloyd H D.Magnetics design for switching power supp lies[M].Texas Instruments Incorporated，2001

[5] 绪方胜彦.现代控制理论[M].北京：科学出版社，1978

[6] 孙定浩，朱德懋，廖炯生.直流变换器的最大磁化电流理论[J].自动化学报，1979，5(1)： 63-74

[7] 孙定浩.一类最佳调节器的综合[C].信息与控制，1980，9(1)：66-73

[8] 孙定浩.推挽变换器的运行环理论[C].中国电源学会第九届全国电源技术年会，天津，1991

Newly Established Operational Theory of Forward Converters

SUN Dinghao， ZHANG Yang， YE Dongdong
(Beijing Institute of Control Engineering， Beijing 100190， China)

Forward converters are characterized by two models different from the traditional model.One of them is that the magnetic reset function is realized by using LC series resonance.In thismodel there is no magnetic reset winding，a capacitor paralleled with the switching device exists.The other is that the magnetic reset function ismainly realized by using the resetwinding.In thismodel there is themagnetic recycle winding，the capacitor paralleled with the switching device exists too both models are analyzed.By means of the phase plane analysismethod，a lot of analytical expressions of parameters of both electric circuits and magnetic circuits when forward converters are operating.These analyses and results here and followed papers are called “newly established operational theory of forward converters”.

forward converter； phase plane analysis；circuit