线性定常系统点位控制时的非线性控制器设计
2011-04-17关轶峰李铁寿郭建新
关轶峰,李铁寿,郭建新
(1.北京控制工程研究所,北京 100190;2.空间智能控制技术重点实验室,北京 100190)
点位控制,也称点到点的控制,即要求系统的输出由初始位置机动至目标位置.这种点位控制在航天器控制、机器人控制及其他工业生产中是非常常见的.一般来说,控制器设计者希望系统输出能以较快的速度到达指定位置,并在该位置处尽快稳定下来.国内外学者对此进行了大量的研究工作,如文献[1]给出了模糊逻辑控制律,文献[2]设计了基于神经网络的控制算法.对于工程设计人员而言,通常选用简单的常系数状态反馈控制律.但是由于其系数是定常的,这种控制律很难同时满足快速性与稳定性能之间的要求.
为解决上述矛盾,文献[3]给出一种非线性积分的控制方法,文献[4]也给出一种变控制器系数的方法,这两中方法都没有给出稳定性的证明.文献[5]提出一种非线性微分的控制方法,这种方法只适用于双积分环节.本文在文献[5]基础上,提出一种非线性控制律设计方法,将被控对象扩展至高阶线性定常系统.控制效果得到进一步提高,而且还分析了闭环系统的稳定性,解决了快速性与在目标位置处尽快稳定之间的矛盾.文章最后给出了数学仿真结果,验证了该方法的有效性.
1 非线性控制思想

图1 输出曲线示意图
基于上述思想设计双积分环节的非线性微分控制律[5]
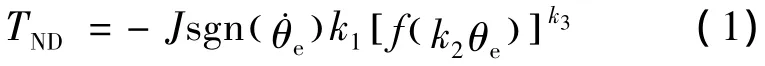

图2 非线性微分控制示意图
非线性微分控制律的根本思想在于,如何得到如图2所示的控制律,并保证系统的稳定性.在式(1)中存在输出速度的符号项sgn(),系统输出可能会出现振颤现象.下面设计的控制律,避免了该问题的出现.
2 高阶线性系统的非线性控制律设计
基于双积分环节的非线性微分控制思想,本节将其方法推广至高阶线性定常系统的点位控制中.
SISO能控线性定常系统

控制律为

其中,状态反馈控制

其中xe=x-xr,xr为期望状态,K为状态反馈矩阵.基于文献[5]中的非线性微分控制设计思想,设计针对系统(2)的非线性控制

其中ye=y-yr,yr为期望输出;f( x)>0(i=1,2,3).非线性控制(5)的设计是在状态反馈控制(4)的基础上,根据输出来调节控制输入,避免系统振荡,达到快速收敛的效果.控制律(5)中的X与状态变量相关,同时兼顾闭环系统的稳定性,其构造形式及稳定性证明,如定理1所示.
定理1.SISO能控线性定常系统(2),基于控制律(3)和(4),存在非线性控制(5),使得由式(2)~(5)组成闭环系统是渐近稳定的.
证明.定理的证明兼有构造性,即如何求得式(5)中的X.不失一般性,设零点为系统的平衡点,即xr=0,xe=x.由式(2)~(5)组成闭环系统

构造正定 Ляпунов 函数 V(x)=xTPx ,则有

构造X=xTPb,则


从上述分析过程总结高阶线性定常系统非线性控制律设计过程:
(1)求取状态反馈矩阵K使A-bK是稳定的;
(2)寻找正定对称矩阵P,使得 ( A-bK)TP+P( A-bK)=Q为负定,可取Q=-I;
(3)由(2)中求得的P构造X=xTPb,得到非线性微分控制律(5)的形式.
几点说明:
(1)非线性微分控制律是在状态反馈控制基础上来改善稳定性能,因此状态反馈的设计对最终的控制效果有一定影响.
(2)Q矩阵选取的不同,控制律的形式将有所不同.文献[5]给出了双积分环节的非线性微分控制律,如果按本文的非线性控制律设计过程也是可以得到的,只是Q矩阵不再是 -I.
3 仿真研究
考虑3阶线性定常系统


其中xe=x-xr,xr=[100]T为期望状态,K=[511]为状态反馈矩阵.
设计非线性微分控制器

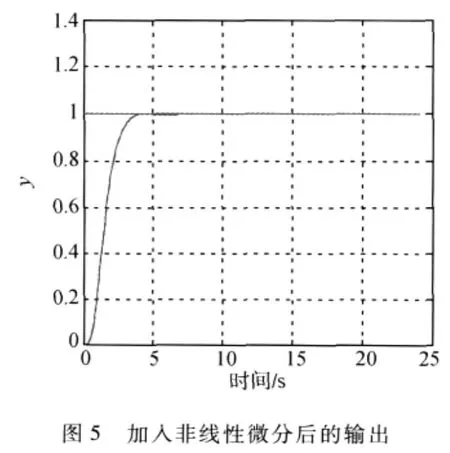
各参数意义见第2节.输出期望值yr=1,k1=10,k2=0.1,k3=1.仿真结果如图3~6所示,图3和4为状态反馈输出及控制输入,图5和6为加入非线性微分后的输出及控制输入.仿真结果显示了非线性微分在改善系统动态性能方面的作用.


4 结论

线性定常系统在点位控制中,常规线性状态反馈控制不能同时实现系统的快速性与良好的稳定性能.本文将文献[5]中提及的非线性微分控制方法推广至高阶线性定常系统的控制,并给出稳定性证明.仿真结果表明了该方法在改善系统动态性能方面的有效性.
[1] Sylvia K R,Flashner H.Stable fuzzy logic design of point-to-point control for mechanical systems[J].Fuzzy Sets and Systems,2000,110(3):389-411
[2] Kottas J.Autonomous neural network controller for adaptive material handling[R].ADA248944,1992
[3] 吴宏鑫.全系数自适应控制理论及其应用[M].北京:国防工业出版社,1994
[4] 牛景汉,颜玉崇.自动控制系统非线性校正[M].北京:机械工业出版社,1992
[5] 关轶峰,李铁寿,王典军.航天器附件大角度快速机动的一种控制方法[J].中国空间科学技术,2004,24(4):1-5
[6] 郑大钟.线性系统理论[M].北京:清华大学出版社,1990
