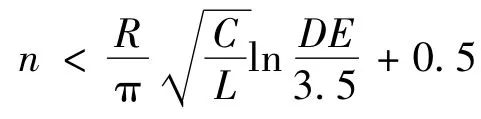一类隔离驱动电路的“剩余驱动”问题
2011-04-17孙定浩
彭 政,孙定浩
(北京控制工程研究所,北京 100190)
隔离驱动电路常应用于直流变换器中,它将PWM电路输出信号与受控MOS管相连,隔离并驱动MOS管,适用于驱动信号与受控器件需要隔离的地方.图1(a)、(b)示出一类典型的隔离驱动电路,文献[1-3]专门对该隔离电路的隔离驱动原理进行分析.本文专注于它在正常运行中当PWM电路收到关闭信号后,这类驱动电路在受控MOS管栅极产生的驱动信号(命名为“剩余驱动”).说明了它对变换器可能造成的危险.文中提出4种改进这类驱动电路以消除这些危险的方法.
1 讨论的问题
图1(a)中用变压器T1将PWM电路与受控MOS管作电气隔离.T1原边的信号通过电磁耦合传输到副边.由于PWM电路输出信号Vo是单向脉冲方波,含有直流分量=DE(单向脉冲的平均值,其中D为占空比,E为PWM电路供电电源电压),故Vo不能直接与 T1的 N1并联,现用电容C隔离,电容C电压左正、右负.Rs用于防止MOS管栅极等效串联电感与栅源间寄生电容产生高频串联谐振.R是栅源间泄漏电阻,目的是提高MOS管抗干扰能力.这样,当PWM电路的输出Vo为高电平(E)时,N1的外加电压为E-=(1-D)E,这个值即Vg高电平的近似值.当Vo为低电平(0)时,C与 N1并联,因此 Vg的低电平的近似值为:-=-DE.值得注意的是Vg的高电平值与占空比D有关,当D大时,Vg高电平值下降,因此这种驱动电路不适合D值变化很大的变换器.

图1 一类典型的隔离驱动电路
图1(b)克服了上述缺陷.当Vo为低电平(0)时,D1将C的电压传递到 C1上,使 VC1= -N2/N1,这样,当Vo高电平时,这个VC1值与由N2传递的感应电压相加,使Vg的正向驱动幅度与占空比无关.值得注意的是,这种驱动电路产生的Vg的低电平为0(图1(a)中Vg的低电平为-DE),因此图1(b)对栅源电容所储电荷的“抽取”能力不及图1(a).

表1 典型隔离驱动电路元器件参数取值范围
表1示出图1电路各元器件参数值的一般可取范围以及本文计算剩余驱动时所用的值(现取值).其中L是T1的初级绕组电感量,暂不考虑磁芯的饱和特性.
设图1(a)(b)已处于正常运行状态,VC=-6V,C存储的能量为3.6μJ.变压器T1磁芯处于对称磁化状态,磁化电流在Ton/2=1μs时刻为0(Ton为Vo的高电平时段),因此磁化电流的最大值为0.018A.磁芯最大储能为,远小于电容C中储能.因此在以后分析中,将正常运行造成的状态近似设定为VC=-6V,im=0.现在要讨论的问题是,在上述状态下,设图1中K接通,PWM电路关闭,即Vo长时间保持为0,图1(a)(b)电路对MOS管产生的Vg的电气特性.
3 剩余驱动的电气特性
设PWM电路在t=0时刻关闭,此时PWM电路的Out端与G端近似短路.由表1知,Rs≤R,在分析剩余驱动时可以忽略.因此,此时的图1(a)的等效电路如图2所示.

图2 图1(a)剩余驱动Vg等效电路
Vg的动态方程是:
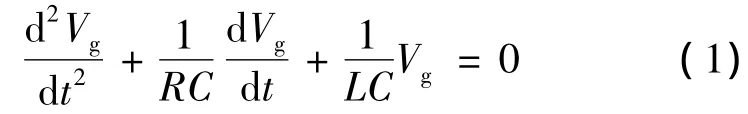
起始条件:

式(1)的特征根为
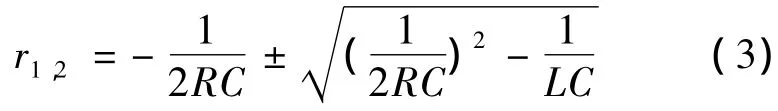

式(1)、(2)的解为
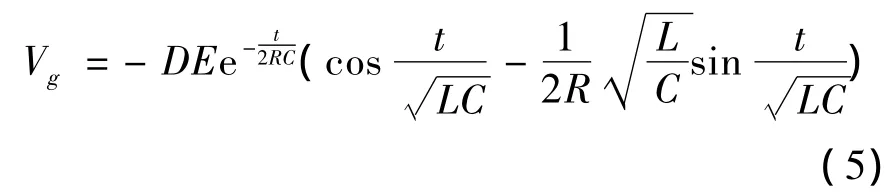
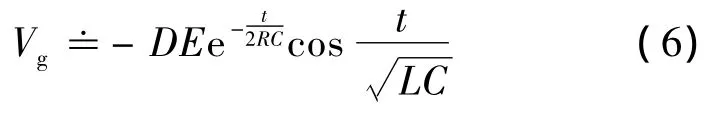
式中指数项的时间常数τ=2RC=4×10-3s,振荡周期图3 示出式(6)描述的剩余驱动.

图3 式(6)描述的剩余驱动
设Q的导通条件是Vg>3.5V,由式(6)可得剩余驱动的电气特性(公式(9)推导见附录):
Vg最大正向驱动幅度:

Q最大导通宽度:

Q总导通次数:

利用电子线路仿真软件Saber,对上述电路进行仿真,其电路图如图4所示,Vg的电压仿真波形如图5~7所示.




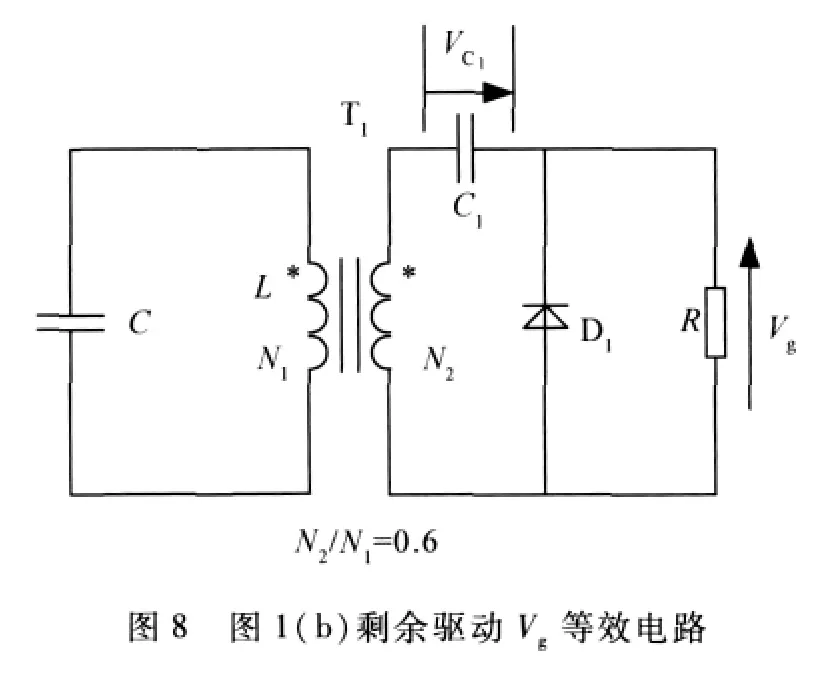
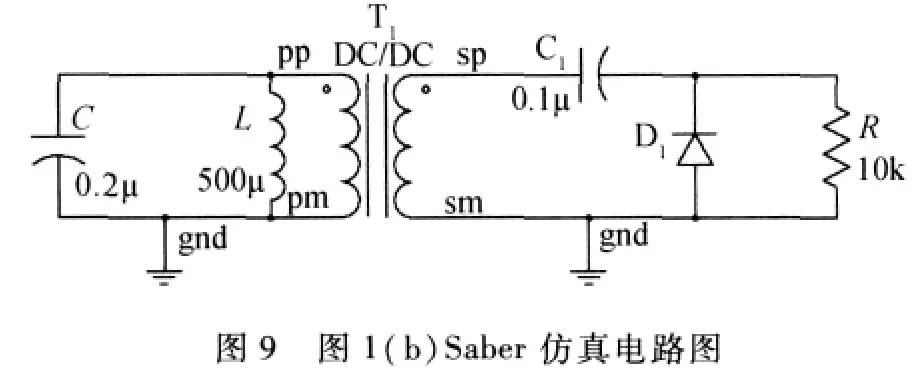
现在定性讨论图1(b)的剩余驱动,其等效电路如图8所示.起始状态VC=-6V,im=0,VC1=3.6V.在图3所示的AB过程中,由于RC1时间常数RC1=0.1 ×10-6×104=1000μs,远大于 AB 过程的15.7μs,所以 D实际处于断开状态.仅从 C1向R放电考虑,A点 VC1=3.6V,B点 VC1_B=在图3的BC过程,可以近似认为Vg是BC曲线乘以0.6与B点上述值相加,最大值为对上述电路进行仿真,其电路图如图9所示,Vg的电压仿真波形如图10、图11所示.由此可见,图1(b)的剩余驱动比图1(a)严重.


4 剩余驱动的危险性
若图1(a)(b)电路用于单端正激变换器(f=200kHz,D=0.4).当 PWM 电路关闭时,由式(8)知Q最大导通宽度为18.9μs,这是正常导通宽度2μs的近10倍,变换器的主变压器有饱和的危险.Q在式(9)所示的多次长时导通时有烧毁的危险.

图12 图1(a)(b)电路用于半桥(或全桥)变换器
图12示出这类驱动电路用于半桥变换器,由一个PWM电路的两个输出端分别激励两个驱动电路.正常运行时,这两个输出端轮流置高电平,产生的驱动信号不会造成Q1和Q2共同导通.但当PWM电路关闭时,这两个驱动电路产生的剩余驱动使Q1和Q2共同导通,变换器电源被Q1和Q2短路.这股大电流有烧毁这两个MOS管的危险.
5 消除(或削弱)剩余驱动的方法
图13示出4种消除剩余驱动的方法.
方法1:图3中Vg起始为负,其变正是经历了这样两步:第一步,C中能量释放到L中,直至C中能量释放完毕,Vg=0;第二步,L中能量释放到C中,在这过程中VC变正,逐渐上升.释放到C中的最大能量就是L中能存储的最大能量.因此,可利用L的磁饱和特性来限制第一步L中能存储的最大能量,来限制第二步Vg能升高的最高电压.前已假设当Vg>3.5V时Q导通,由于下式得第二步C允许的最大储能为:,引用符号is为 L的饱和电流,当他满足下列条件:,即is<0.07A剩余驱动将不会造成Q导通.C起始能量与L饱和能量的差将以大电流脉冲的方式耗散在L的绕组中和磁芯中.

图1 34种消除剩余驱动的方法
对上述电路进行仿真,其电路图如图14所示,假定饱和磁芯采用飞利浦公司3E2A材质,初始磁导率为4500,饱和磁通密度为340mT.由最大存储磁能maxW=1.23μJ可得,磁芯的体积V应满足下列公式:
由上式得:
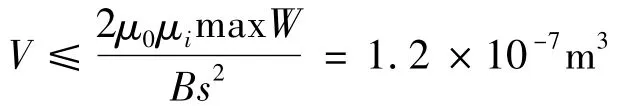
有效磁路面积设为Ae=10×10-6m2,有效磁路长度设为Le=1.0×10-2m.为满足电感量的要求,其绕组匝数N应满足下列方程:
线圈匝数设为9匝.Vg的电压仿真波形如图15所示,由图可见,当变压器饱和时,变压器原边产生大电流,能量耗散在变压器的绕组和磁芯中,由于磁芯存储的能量小于1.23μJ,在Vg变正时,其幅值已经小于3.5V.该方法可以很好地抑制Vg的电压.
方法2:将图1(a)(b)中Rs左移至如图13(b)所示.产生这一思路的物理基础是图3和图8的LC回路中没有消耗能量的电阻,将Rs移至与C串联,既能起前已叙述的抑制高频串联谐振的作用,又使LC回路形成LRsC回路.

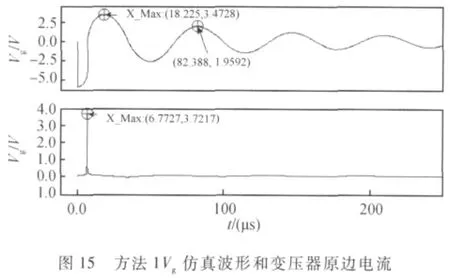

图16的动态方程是:

式中:

起始条件是:

下式依然成立
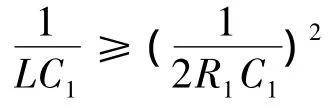
故式(10)~(13)的解为:


注意到式(14)中正弦的系数为0.1,得图16剩余驱动的近似式为:
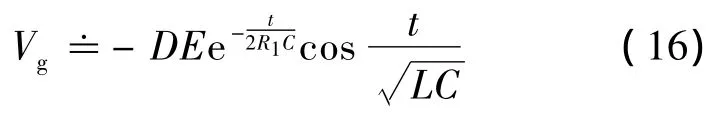
由上式得Vg的电气特性:
Vg最大正向驱动幅度:DEe
对上述电路进行仿真,其电路图如图17所示,Vg的电压仿真波形如图17所示,由图可见,该方法可以很好地抑制Vg的电压.
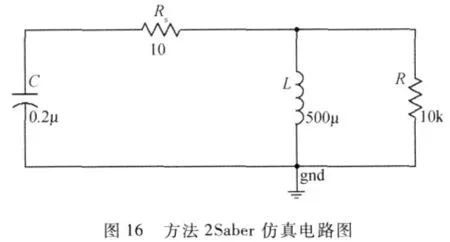

若将 Rs提高为15Ω,则正向驱动幅度约为3.8V,其Vg的仿真波形如图18所示,这对变换器已不造成危险.由此可见图1中Rs左移的作用.

图18 方法2Vg仿真波形
方法3:图13(c)C并联二极管D1,它不影响PWM电路正常运行.但它使C的正向电压钳位在二极管的正向导通压降.
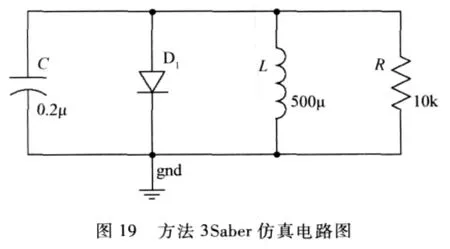
对上述电路进行仿真,其电路图如图19所示,Vg的电压仿真波形如图20所示,由图可见,Vg的电压最大值为0.78V,该方法消除了图1(a)剩余驱动的危险性.

方法4:对图1(b)可采用图13(d)所示方法消除剩余驱动的危险性.二极管D1使C产生的正向驱动电压在Vg的正向驱动电压中仅增加0.6N2/N1=0.36V.Vg正向电压的另一分量由 C1产生(t=0时VC1=3.6V),可适当减小 R,利用图3所示AB过程这段时间衰减至允许值.例如取R=1kΩ,经 AB 这段时间15.7us,VC电压已衰减为
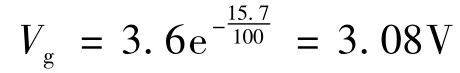
此时,剩余驱动已不能使Q导通.电容C1并联电阻R1也是加速C1正向衰减的可用方法.
对上述电路进行仿真,其电路图如图21所示,其中C1并联电阻R1设为510Ω,Vg的电压仿真波形如图22所示,由图可见,Vg的电压最大值为3.02V,该方法消除了图1(b)剩余驱动的危险性.如果将R1的电阻减小到51Ω,Vg的电压最大值下降到0.74V.


6 结论
本文的讨论具有这样的启示:对包含了储能元件的开关驱动电路,应谨慎评估它在PWM电路关闭后可能存在的“剩余驱动”,严防其对变换器可能产生的潜在危险.本文提出的图13所示的4种消除剩余驱动危险的对策,可单独或综合使用.其中方法1简单,但是磁芯损耗大;方法2简单,但是只能减少剩余驱动危险;方法3较复杂,但是能消除剩余驱动危险.
[1] 丁道宏.电力电子技术[M].北京:航空工业出版社,1999
[2] Bell B.Digital isolators:a space-saving alternative to gate-drive transformersin DC-DC converters[J].HOW2POWER,2010
[3] 王华彪,陈亚宁.IGBT和MOSFET器件的隔离驱动技术[J].电源技术应用,2006,9(5):43-45
附 录
公式(9)推导如下:
设Q的导通条件是Vg>3.5V,根据公式(6)得出:
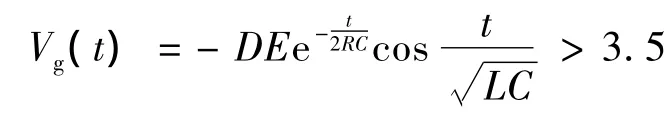
如图23所示,计算Vg(t)的上包络线值,将上式中“t”用振荡周期表示,即:t=(n-

图23 Vg(t)波形
代入上式得:

得到Q的导通次数为: