刚体卫星姿态的有限时间控制*

2011-11-24李贵明刘良栋

空间控制技术与应用 2011年3期

关键词：姿态控制角速度扰动

李贵明，刘良栋

(1.北京控制工程研究所，北京100190；2.空间智能控制技术重点实验室，北京100190)

刚体卫星姿态的有限时间控制*

李贵明1，2，刘良栋1

(1.北京控制工程研究所，北京100190；2.空间智能控制技术重点实验室，北京100190)

针对刚体卫星的姿态控制问题，设计了不存在和存在扰动力矩两种条件下的有限时间状态反馈控制律.对于无扰动力矩情形，基于非线性齐次系统性质，设计了一种便于工程实践性的连续、非奇异的比例微分形式控制算法，保证姿态闭环系统有限时间收敛到零点，而且此算法能直接推广到卫星姿态跟踪问题.对于存在扰动力矩的情形，基于有限时间Lyapunov定理设计的连续、非奇异的控制力矩保证卫星姿态和角速度在有限时间内收敛到原点附近的部域.当外扰力矩为零时，此控制律使闭环系统状态有限时间收敛到平衡点.数学仿真结果说明了提出的控制算法有效.

卫星姿态控制；有限时间稳定；扰动力矩；非奇异

卫星姿态控制是自动控制领域内的一个重要的研究方向.近年来，该领域取得了许多成果，如 PD形式的姿态控制[1]，滑动模态控制[2]，自适应控制[1，3]，基于无源性的欠角速度测量条件下姿态控制器设计[4-5]、四元数观测器设计[6]，扰动抑制问题[7]和姿态同步控制问题[8].

上述的闭环控制系统固然是稳定的，但遗憾的是仅仅取得了渐近稳定性，即闭环系统状态要在时间趋于无穷大时才能收敛到零.比较系统的响应时间可知，有限时间控制律具有更好的动态性能以及良好的鲁棒稳定性和扰动抑制效果[9-10].由于文献[11]中的有时时间控制律的不连续性可能导致颤振问题，Haimo设计了双积分系统的时不变连续状态反馈控制器[12]，但此控制量无上限，而且仅适合此类形式的被控对象[13].因此，文献[13]基于Lyapunov有时时间稳定性定理[14]设计了双积分系统有上限的全局有限时间连续状态反馈控制器.Hong[15]基于有限时间观测器研究了双积分系统的有限时间输出反馈控制问题，而且设计的控制器对于满足一定条件的一类不确定性或外部扰动具有鲁棒性.此外，Hong还解决了一类链状系统的有限时间控制问题[16]，Huang[17]基于文献[18]的研究设计了一类具有不确定性的链状单积分系统的有限时间控制器.

有限时间控制技术应用方面，Hong[19]设计了机械臂系统的PD形式有限时间控制器，Su将其扩展到跟踪情况[20].对于卫星姿态控制问题，文献[21]和[22]均借用滑动模态设计控制器，但很明显，这些控制器因存在误差变量的负次幂而具有奇异性，亟待改善.而且，[22]仅能保证性能收敛在滑模面附近.Ding[23]解决了有扰条件下卫星姿态有限时间调节问题，然而，其设计方法仅适合于对角形式的惯量阵，且控制算法不具有连续性，设计复杂，因此，有必要进一步研究卫星姿态的有限时间控制问题.

为改善前述[21-23]的刚体卫星姿态有限时间控制律不连续、存在奇异性、设计复杂、应用范围严重受限的弊端，本文研究了形式简单、具有连续性和非奇异性的刚体卫星姿态的有限时间控制器设计问题，提出了不存在扰动力矩和存在扰动力矩两种条件下的有限时间状态反馈控制律.针对理想无扰情形，基于非线性齐次系统性质设计的比例微分形式(PD)控制算法，保证了闭环姿态控制系统有限时间收敛到零点.连续、非奇异的有限时间PD控制器一般化了传统PD控制器，当幂指数为1时，有限时间退化为渐近稳定控制器，即说明基于无源性设计的传统PD控制律为有限时间控制算法的特例；针对存在扰动力矩的情形，基于有限时间Lyapunov定理设计的控制力矩保证卫星姿态和角速度在有限时间内收敛到原点附近的邻域.此有限时间控制器不仅具有连续性、非奇异性的特点，而且设计过程简单，适合于更具一般性(惯量矩阵非对角形式)的卫星系统.

1 系统与问题描述

1.1 有限时间稳定定理

首先给出有限时间稳定的相关定义[10].考虑如下的非线性系统

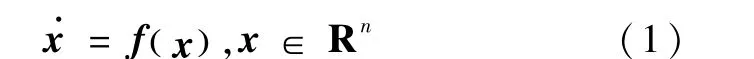
式中，f(x)是连续函数，且f(0)=0.如果系统(1)是Lyapunov稳定的，而且，存在一个时间函数T(x)，使得对于所有的 t≥ T(x)，有 x(t)=0，则称系统(1)是有限时间稳定的；如果具有全局性，则称全局有限时间稳定.

为便于后续分析，这里引入齐次函数的定义.对于连续函数 V(x)和 ( r1，…，rn)∈ Rn，ri＞0，如果对于任意的ε＞0，存在标量k，满足

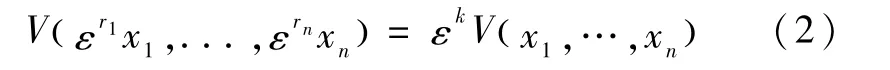
则称系统(1)关于 ( r1，…，rn)具有齐次度k.

引理1[10].如果系统(1)具有负的齐次度，即k＜0，并且其原点具有渐近稳定性，那么系统(1)的原点是有限时间稳定的.

引理2[15].对于系统=f(x)+(x)，f(x)关于( r1，…，rn)具有负的齐次度 k，同时(0)=0.假设x=0为=f(x)的渐近稳定平衡点，同时

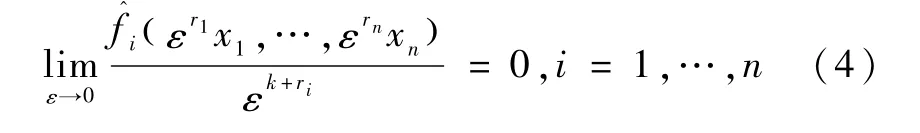
对于任意x≠0成立，那么x=0为此系统的一个局部有限时间平衡点.

引理3[14].考虑系统(1)，如果存在一个定义在含原点的开集amp;上的连续正定函数V，且存在实数k＞0和 α∈ ( 0，1)，使得+k≤0 ，则系统(1)的原点是有限时间稳定的，而且调节时间的一个估计值为

引理4[17-18].对任意实数x、y，以及正实数c和d，存在如下关系

令b=p/q≤1，其中p和q都是正奇数，那么

对于0＜a≤1，存在

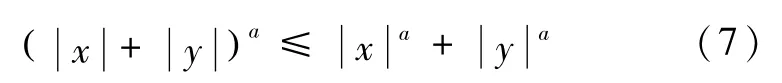
1.2 卫星姿态运动

本文采用修正罗德里格斯参数[5，24](MRP)描述刚体卫星相对于惯性坐标系I的姿态.定义卫星姿态为，那么基于MRP的卫星姿态运动学方程为

表示 σ的反对称矩阵.为解决 MPR在±2π处的奇异性问题，文献[25-26]阐述了原始集σ与相应的映射集σs相结合的方法，即定义映射集 σs=-σ/(σT)σ，当时将σ映射到σs上，故而对于任意变化的姿态角，使σ或σs处于单位圆内.需要指出的是，σ和σs描述相同的卫星物理姿态，而且σs同样满足运动学方程(8)，即=Gσ( )sω.因此，仅通过研究即可实现MRP的全局非奇异性.

刚体卫星在其本体坐标系B下的姿态动力学方程为

定义期望的卫星姿态指令为 σd，对应的坐标系为D，记卫星相对于姿态指令的姿态误差为，则有

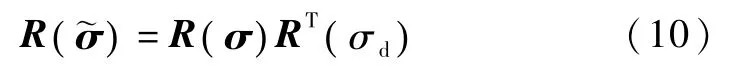
式中，R(·)为方向余弦矩阵.定义期望的卫星角速度为ωd，记卫星相对于角速度指令的误差=ω-R()ωd，则卫星姿态误差运动学方程为

相应的姿态误差动力学方程为

本文的控制问题描述为：在不存在外扰力矩情况下设计卫星姿态连续、非奇异的有限时间控制律，保证卫星姿态和角速度在有限时间内收敛到原点；当存在外扰力矩时，设计连续、非奇异的有限时间卫星姿态控制律，保证姿态和角速度在有限时间内收敛到原点邻域.

2 无扰动作用时的有限时间控制器设计

运动学方程(8)可写为

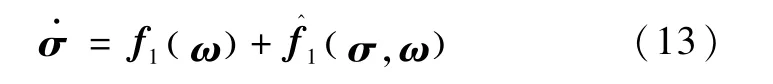
设计PD形式的控制力矩

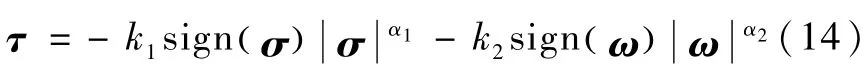
式中，0 ＜α1＜1，α2=2α1/1+α( )

1，k1、k2为增益，sign(·)为符号函数，的运算规则为

式(14)代入式(9)，得闭环系统动力学方程

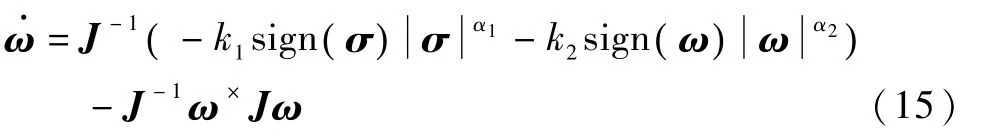
即

性质1.系统(17)

是有限时间稳定的.

证明.取备选Lyapunov函数

那么

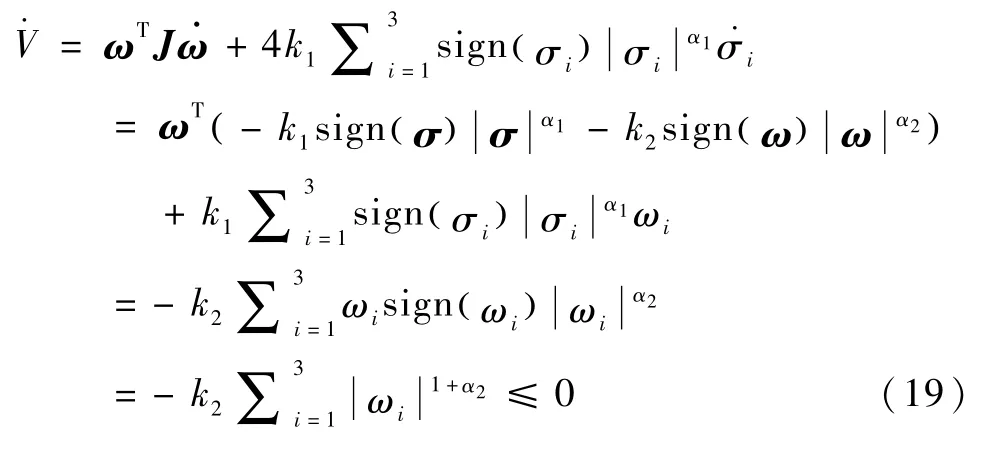
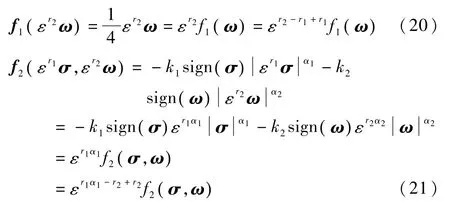
式中， r2α2=r1α1.取 r1α1-r2=r2-r1，那么对于r2=1则有，且.因此，系统(17)具有负的齐次度 k，根据引理1，系统(17)的平衡点 σT，ω(T)T=0具有有限时间稳定性.证毕.

对于任意的 σT，ω

(T)T≠0，考虑到

同理有

又由于

则根据引理2， σT，ω(T)T=0是卫星姿态控制系统(8)和(9)的有限时间平衡点.上述的分析得到本文第一个结论.

定理1.针对无扰动力矩作用的卫星姿态控制系统(8)和(9)，设计的连续、非奇异 PD形式有限时间控制器(14)，保证了姿控系统的所有信号有界，而且闭环系统的平衡点具有有限时间稳定性.

注1.控制律(14)具有连续、非奇异的特点，而且形式简单，不受被控对象特点限制，因此，式(14)是无扰动力矩作用时最具工程实践性的有限时间控制器.

注2.当参数α1=1时，式(14)特殊化为传统形式的PD控制器τ=-k1σ-k2ω，可见，渐近稳定控制律可视为有限时间控制律在T→∞时的特例.但由于我们并未找到直接的Lyapunov函数，即上述的证明过程不同于传统PD控制下系统稳定性证明，因此，仅通过上面的分析还不能严格地从理论上说明有限时间稳定的全局性，而且不能对存在外部扰动力矩的情况进行分析.当然，如果扰动力矩满足

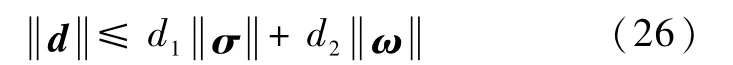
式中，d1和d2为正实数.那么，基于上述分析过程仍然可以得到闭环系统的有限时间稳定性.

注3.设计的PD形式的控制算法容易推广到姿态跟踪问题.即

定理2.对任意给定的时变姿态指令σd，控制力矩保证姿控系统所有信号有界，并且，卫星姿态能在有限时间 T内跟踪 σd，即当 t≥ T时，

为分析更具一般性的扰动力矩作用下卫星姿态系统特性，引入下一节的内容.

3 存在扰动力矩时的有限时间控制器设计

当外扰力矩d≠0时，我们基于一类非线性系统[18]和[17]提出的设计方法构造 Lyapunov函数，并设计控制力矩，保证卫星姿态在有限时间内收敛到原点邻域；对于其特例d=0，可知卫星姿态在有限时间内收敛到原点.为便于分析问题，我们首先假设d=0，然后扩展到d≠0的情况.

基于上述变量设计控制力矩形如

式中，m＞0为待设计的控制增益.将控制力矩(28)代入姿态控制系统，得到闭环系统运动特性

定理3.卫星姿态闭环系统(29)的所有信号有界，而且，姿态角σ和角速度ω在有限时间内收敛于原点；当控制律(28)中的σ和ω为误差信号时，可以实现卫星姿态角对任意时变参考指令σd()t的有限时间跟踪.

证明.对于，有

定义常数r()t=σTσ，则有r()t≥0，故上式可写成

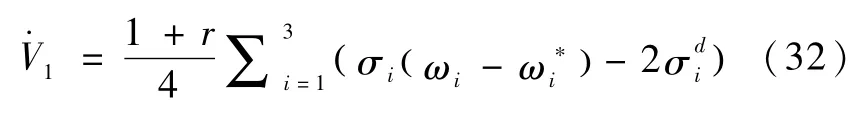
定义 ζ1=σ1，那么

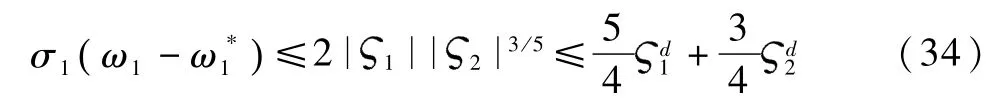
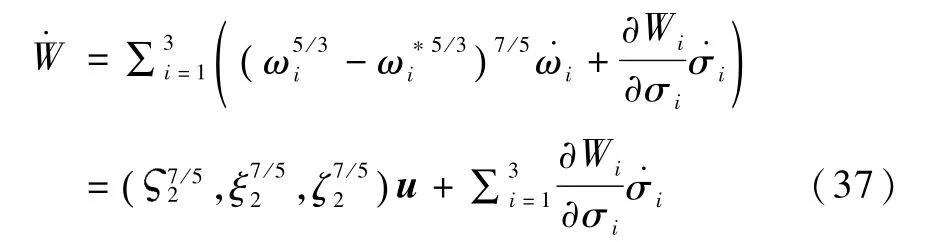
取备选Lyapunov函数为V=bV1+W，b＞0，那么

性质2.对于 i=1，…6，存在实数 ci＞0，c=c1，…，c( )

6，定义向量则有

由于

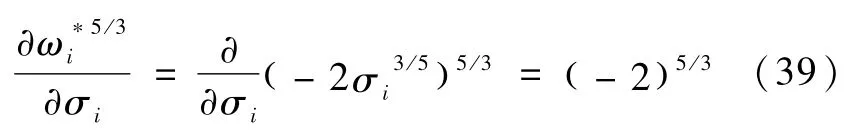
以及定积分中值定理

那么可得

式中，k=14/5·(2).

考虑运动学特性(8)，以及约束 σ ＜1，可知上式中的第一项

那么

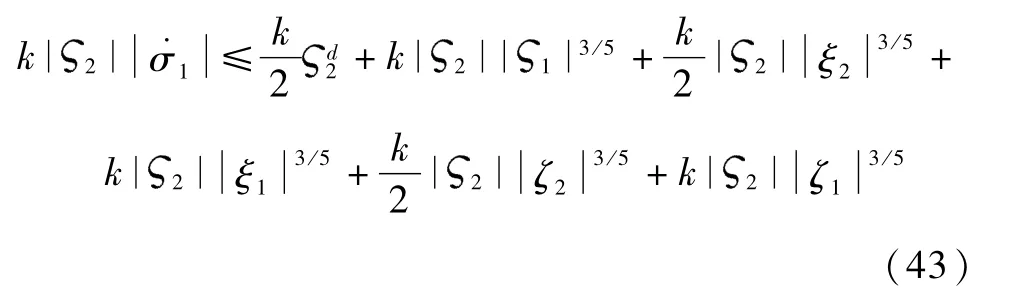
利用引理4，可知同理分析式(41)中的后两项.因此，性质2成立.以一组保守的参数估计进行控制器设计，取

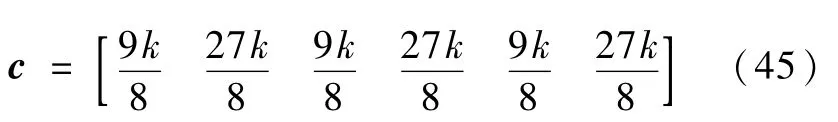
那么式(38)可以写成

同时，对于V=bV1+W，由引理4可知

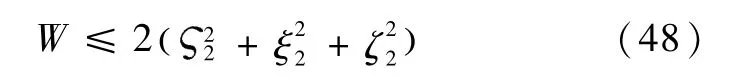
则显然有

取参数α=4/5，根据引理4有

d≤ l，l＞0，则式(47)改写为

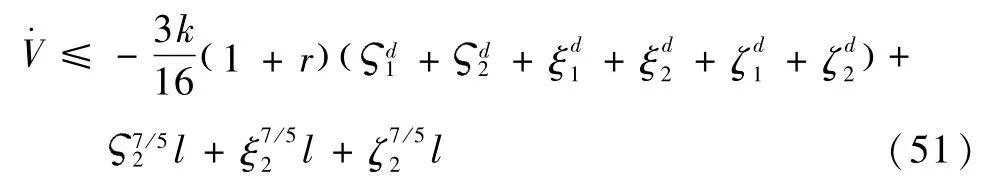
下面研究存在上限的外部干扰力矩d时，系统特性.假设 J-1上式描述了有限时间意义下的最终有界性问题，文献[22]称之为实际有限时间稳定.显然，存在0＜β≤1，使得

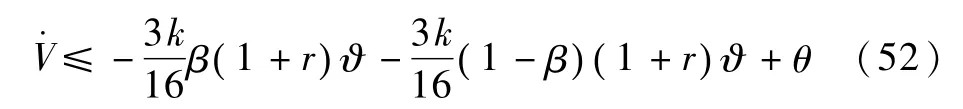
下面借鉴文献[9]和[23]的分析，估计姿态角σ和角速度ω的收敛区域.()ω∈Ω，那么根据

同理确定ω2和ω3的收敛区域，因此有ω∈Δ，Δ为

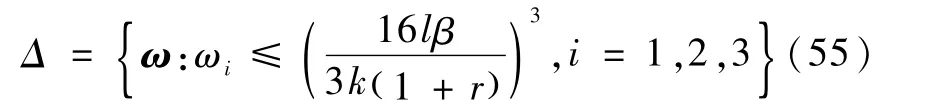
注意到0≤r()t＜1，故令r()t=0，即可得系统状态收敛区域 Γ和 Δ的保守估计，进而得到下述性质.

定理4.当卫星姿态系统中存在有上界约束的外扰力矩时，控制力矩(28)能保证姿态闭环系统稳定，而且，姿态角σ和角速度ω在有限时间内收敛到原定附近的邻域内，即当时，有σ()t∈ Γ，ω()t∈ Δ.

注4.上述的证明说明，文献[17]的约束条件(其公式3.1)过于严格.也就是说，不确定项的约束条件可以不受限于上三角形式，即可以将基于反步法的有限时间控制技术推广到更具一般性的一类非线性系统.

注5.由于 r()t=σTσ，因此控制器(28)中参数具有时变特性，不便于系统实现.可以通过直接取r=1进行控制律设计，上述的证明过程仍然成立.本文直接采用文献[17]中的指数次方，实际上，通过改变Lyapunov函数及相关变量定义中的指数次方，可以调节控制律(28)中的幂指数.同渐近稳定控制律一样，控制律(28)同样可以通过调节控制参数增益的方式来缩小收敛区域，但可能存在控制量饱和问题.文献[23]认为，有限时间控制律的优势在于，能在保证控制不饱和的条件下，通过改变幂指数来减小系统状态的收敛区域.尽管如此，控制律(28)饱和问题仍值得进一步研究.

4 数值实例

取α1=0.5，k1=6，k2=10，则控制力矩(14)作用下的卫星姿态和角速度随时间变化如图1和图2所示.

图1 PD形式有限时间控制器作用下的卫星姿态

图2 PD形式有限时间控制器作用下的卫星角速度

取式(28)中m=50，约束饱和力矩为10N·m，则无扰动力矩时卫星姿态如图3所示.设扰动力矩为d(t)=8sin( 2πt)·[1.0，1.2，1.0]TN·m，则此时力矩(28)作用下的卫星姿态、角速度如图4和图5所示.

图3 无扰动力矩时控制律(28)作用下的卫星姿态

图4 存在扰动力矩时控制律(28)作用下的卫星姿态

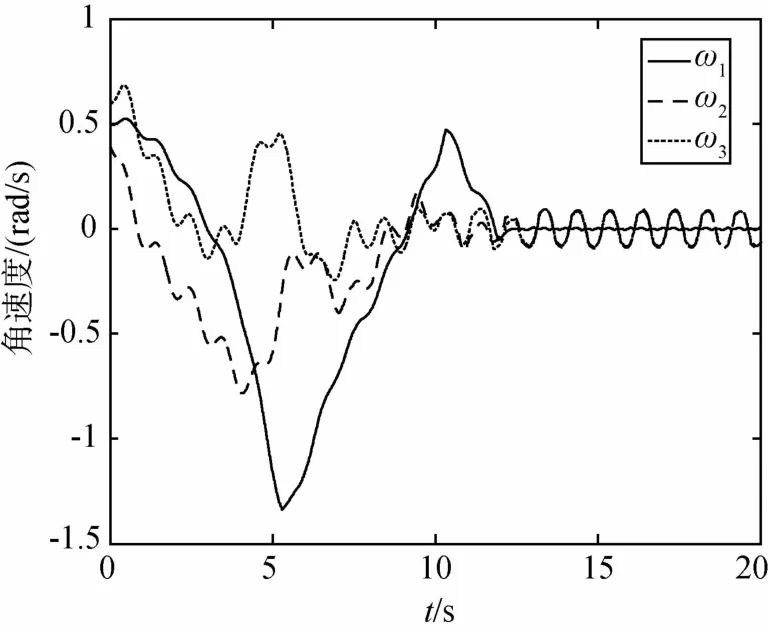
图5 存在扰动力矩时控制律(28)作用下的卫星角速度

6 结论

本文研究了不存在和存在扰动力矩两种条件下，卫星姿态的有限时间状态反馈控制律设计问题.对于无扰动力矩情形，设计了便于工程实践性的连续、非奇异的比例微分(PD)形式控制算法，保证了姿态闭环系统有限时间收敛到零点；对于存在扰动力矩的情形，基于有限时间Lyapunov定理设计的连续、非奇异的控制力矩能够保证卫星姿态和角速度在有限时间内收敛到原点附近的邻域.然而，PD控制器形式下的有限时间Lyapunov函数还有待于寻求，其有限时间收敛的全局性还有待证明；基于构造法设计的控制律存在着相对严重的饱和问题，也亟待解决.

[1] Wen J T，Kreutz-Delgado K.The attitude control problem[J].IEEE Transactions on Automatic Control，1991，36(10)：1148-1162

[2] Chen Y P，Lo S C.Siliding-mode controller design for spacecraft attitude tracking maneuvers[J].IEEE Transactions on Aerospacecraft and Electronic Systems，1993，29(4)：1328-1333

[3] Ahmed J，Coppola V T.Adaptive asymptotic tracking of spacecraft attitude motion with inertialmatrix identification[J].Journal of Guidance， Control， and Dynamics，1998，21(5)：684-691

[4] Lizarralde F，Wen J T.Attitude control without angular velocity measurement：a passivity approach[J].IEEE Transactions on Automatic Control， 1996， 41(3)： 468-472

[5] Tsiotras P.Further passivity results for the attitude control problem[J].IEEE Transactions on Automatic Control， 1998， 43(11)： 1597-1600

[6] Tayebi A.Unit quaternion-based output feedback for the attitude tracking problem[J].IEEE Transactions on Automatic Control， 2008， 53(6)： 1516-1520

[7] Cheng Z Y，Huang J.Attitude Tracking and Disturbance Rejection of Rigid Spacecraft by Adaptive Control[J].IEEE Transactions on Automatic Control， 2009，54(3)：600-605

[8] Lawton JR，Bread RW.Synchronized multiple spacecraft rotations[J].Automatica，2002，38(8)：1359-1364

[9] Bhat SP，Bernstein D S.Finite-time stability of continuous autonomous systems[J].SIAM Journal of Control Optimal， 2000， 38(3)： 751-766

[10] Bhat S P，Bernstein D S.Finite-time stability of homogeneous systems[C].American Control Conference，New Mexico， USA， June，1997，2513-2514

[11] Ryan E P.Finite-time stabilization of uncertain nonlinear planar systems[J].Dynamics and Control， 1991， 1(1)：83-94

[12] Haimo V T.Finite time controllers[J].SIAM Journal of Control and Optimal， 1986， 24(7)： 760-770

[13] Bhat S P，Bernstein D S.Continuous finite-time stabilization of the translational and rotational double integrators[J].IEEE Transactions on Automatic Control，1998，43(5)：678-682

[14] Bhat S P，Bernstein D S.Lyapunov analysis of finitetime differential equations[C].In Proceeding of the A-merican Control Conference， 1995， Seattle WA， June，1831-1832

[15] Hong Y G， Huang J， Xu Y S.On an output feedback finite-time stabilization problem[J].IEEE Transactions on Automatic Control， 2001， 46(2)： 305-309

[16] Hong Y G.Finite time stabilization and stabilizability of a class of controllable systems[J].Systemsamp;Control Letters， 2002， 46(4)： 231-236

[17] Huang X Q，Lin W，Yang B.Global finite-time stabilization of a class of uncertain nonlinear systems[J].Automatica，2005，41(5)：881-888

[18] Qian J C，Lin W.A continuous feedback approach to global strong stabilization of nonlinear systems[J].IEEE Transactions on Automatic Control， 2001， 46(7)：1061-1079

[19] Hong Y G，Huang J.Finite time control of robotmanipulators[J].Systemsamp;Control Letters， 2002， 46(4)：243-253

[20] Su Y X.Global continuous finite-time tracking of robot manipulators[J].International Journal of Robust and Nonlinear Control， 2009， (19)： 1871-1885

[21] Jin E D，Sun ZW.Robust controllers design with finite time convergence for rigid spacecraft attitude tracking control[J].Aerospace Science and Technology， 2008，12(4)：324-330

[22] Zhu Z，Xia Y Q，Fu M Y.Attitude stabilization of rigid spacecraft with finite-time convergence[J].International Journal of Robust and Nonlinear Control，in press

[23] Ding SH，Li.SH.Stabilization of the attitude of a rigid spacecraft with external disturbances using finite-time control techniques[J].Aerospace Science and Technology，2009，13(4-5)：256-265

[24] Shuster M D.A survey of attitude representations[J].The Journal of Astronautical Sciences， 1993， 41(4)：493-517

[25] Schaub H，Junkins J L.Stereographic orientation parameters for attitude dynamics：a generalization of the rodrigues parameters[J].Journal of the Astronautical Sciences， 1996， 44(1)： 1-20

[26] 吕建婷.三轴稳定卫星姿态控制算法研究[D].哈尔滨：哈尔滨工业大学，2007

Finite Time Stabilization Method for the Rigid Spacecraft A ttitude Control

LIGuiming1，2， LIU Liangdong1
(1.Beijing Institute of Control Engineering， Beijing 100190，China；2.Science and and Technology on Space Intelligent Control Laboratory， Beijing 100190，China)

For the rigid spacecraft attitude control problem， amethod for designing the finite time controllers is proposed in this paper controllers are analyzed in the absence of disturbance and in the presence of disturbance.For the first case，based on the property of the nonlinear homogeneous system，a continuous and non-singular proportional-derivative(PD)controller is proposed to achieve the finite time convergence of the closed-loop attitude control system，and can be extended to the spacecraft attitude tracking problem.For the second case，we design a new continuous and non-singular controller is design on the basis of Lyapunov finite time theorem，such that the spacecraft attitude and angular velocity converge to a small neighborhood of the equilibrium point.If the disturbance vanishes，all the states will converge to the origin eventually.Last，numerical simulation is conducted to demonstrate the effectiveness of our proposed controller.

spacecraft attitude control； finite time control； disturbances torque；non-singular