一类Poisson分布的数学模型

范洪福

（上海理工大学理学院，上海 200093）

一类Poisson分布的数学模型

范洪福

（上海理工大学理学院，上海 200093）

详细地建立了一种服从Poisson分布的随机变量的数学模型，并作了推广.［关键词］随机变量；Poisson分布；二项分布；相互独立

1 引 言

多年为本科学生讲授《概率论与数理统计》课程，我们积累了一些教学经验.此课程具有丰富的实际背景，应用广泛.在教学中，应当让理论密切联系实际问题，尽量多介绍一些概率模型，分析随机现象，让学生深刻理解有关概念和方法，了解本课程丰富的背景，融会贯通，学以致用.

在概率论中，Poisson分布是一类极其重要的分布，背景特别丰富.这里，我们来建立一类服从Poisson分布的随机变量的数学模型.在课堂教学中，我们曾经多次介绍过此类模型，引起了学生们浓厚的兴趣，从而增强了学习《概率论与数理统计》课程的兴趣，教学效果颇佳.

2 数学模型

我们学校所处的上海市军工路是一条交通主干道中环线，交通繁忙，位于军工路516号的学校大门口每天来往的汽车众多.我们来考察一天内经过本校门口的汽车次数的分布情况.

用随机变量X表示“一天内经过本校门口的汽车次数”.将一天24小时等分成m个时段，每个时段为5秒，每辆车在一个时段内至多经过本校门口一次.再用随机变量Xi表示“第i个时段内经过本校门口的汽车次数”，i＝1，2，…，m，则

且X1，X2，…，Xm近似相互独立.

先考虑Xi的分布.假设有可能经过本校门口的汽车总数为N辆，在这N辆车中，离本校远近分布不同，有的离本校很近，有的较近，有的较远，有的很远.在一个时段内，它们经过本校门口的概率不同.因此，按照距离远近，将全中国分解成n个区域，并设在第j个区域内，共有tj辆车在一个时段内有可能经过本校门口，则有

现提出两个假设条件：

（a）每辆车是否经过本校门口相互独立；

（b）对于属于第j个区域内的tj辆车，在一个时段（假设为第i个时段）内每辆车经过本校门口（记为事件Aij）的概率相等，记P（Aij）＝pij.

由于现在燃油、燃气费昂贵，如果汽车没有事情不会经过本校门口，条件（a）近似成立.由于已将全国区域进行划分，处于同一区域内的汽车离本校远近相当，它们经过本校门口的概率大致相同，条件（b）成立.

现用随机变量Yij表示“在第i个时段内属于第j个区域内的tj辆车中经过本校门口的汽车次数”，j＝1，2，…，n，则有

由条件（a），Yi1，Yi2，…，Yin近似相互独立.

现在首先考虑Yij的分布.

对于属于第j个区域内的tj辆车而言，在5秒内每辆车要么经过本校门口（事件Aij），要么不经过本校门口（事件￣Aij），而且相互独立，故此为tj重Bernoulli试验，事件Aij发生的次数

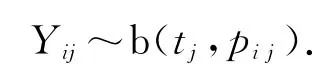
显然，这里的tj很大，tj≥10000；pij很小，pij＜0.1.根据［1］中Poisson定理，近似地有

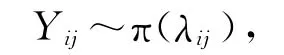
这里λij＝tj·pij.由于Yi1，Yi2，…，Yin相互独立，根据［1］中98页介绍的Poisson分布的可加性，有

由于X1，X2，…，Xm相互独立，再次利用Poisson分布的可加性，有

3 模型推广

以上数学模型可以推广到多种随机现象，从而可知Poisson分布的普遍性.

A.考察一所大学一年内发生的学生违纪处分次数Y.

若把“学生”比拟为“汽车”，“受到违纪处分”比拟为“经过本校门口”，则可以类似地把一年时间等分成m个时段；把全校学生按照违纪概率的大小划分成n个等级.经过类似的讨论、分析，可以说明随机变量Y也服从Poisson分布.

B.考察一家经营机动车辆强制保险业务的保险公司一个月内理赔的次数Z.

若把“机动车”比拟为“汽车”，“发生需要理赔的交通事故”比拟为“经过本校门口”，则可以类似地把一个月时间分成m个时段；把购买该保险公司车辆强制保险的机动车按照发生需要理赔的交通事故的概率的大小划分成n个等级.经过类似的讨论、分析，可以说明随机变量Z也服从Poisson分布.

［1］ 盛骤，等.概率论与数理统计［M］.2版.北京：高等教育出版社，1989.

［2］ Milton J S，Mcteer P M，Corbet J J.Introduction to statistics［M］.Mc Graw-Hill Companies，1997.

A Kind of Mathematical Model of Poisson Distribution

FAN Hong-fu

（College of Science，University of Shanghai for Science ＆Technology，Shanghai 200093，China）

A mathematical model of Poisson distribution is constructed in detail，then it is generalized.

random variable；Poisson distribution；binomial distribution；mutually independent

O29

C

1672-1454（2011）04-0150-02

2008-10-20；

2009-05-18

上海市教委重点课程建设课题《数学物理方程》（2010年-2011年）资助项目