Stewart定理的一个推论及其应用

●

(彭阳县第三中学 宁夏彭阳 756500)

Stewart定理的一个推论及其应用

●王伯龙

(彭阳县第三中学 宁夏彭阳 756500)

1Stewart定理及其推论

Stewart定理已知△ABC及其底边BC所在的直线上一点O(不同于点B,C)，则

|AB|2·|OC|+|AC|2·|BO|-|AO|2·|BC|=

|BC|·|BO|·|OC|.

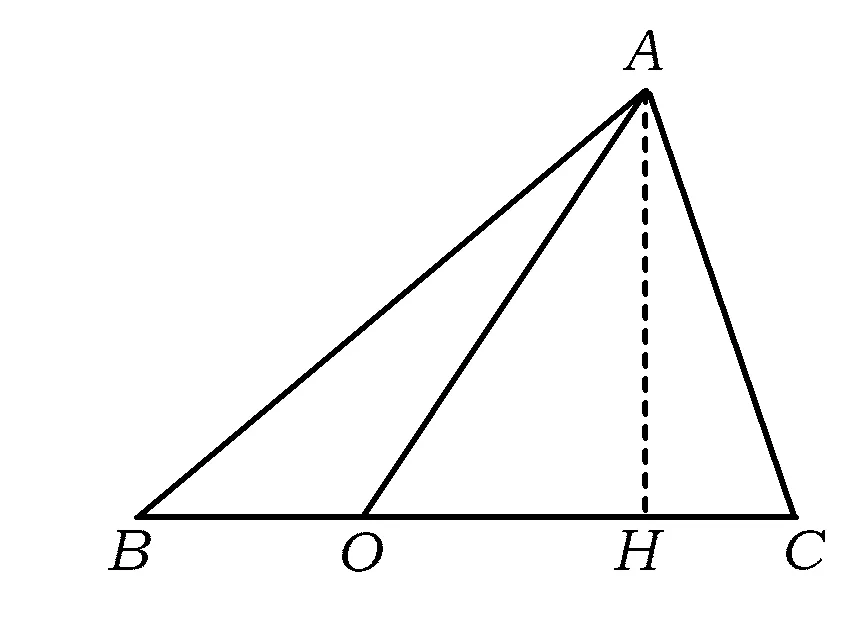
图1

证明如图1，作△ABC底边BC上的高线AH.在△ACO中，由余弦定理得

|AC|2=|AO|2+|OC|2-2|AO|·|OC|·cos∠AOC.

在Rt△AOH中，有

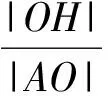
从而 |AC|2=|AO|2+|OC|2-2|OC|·|OH|.

同理，在△ABO中,有

|AB|2=|AO|2+|BO|2+2|BO|·|OH|.

以|BO|和|OC|分别乘上面2个式子，并相加得

|AB|2·|OC|+|AC|2·|BO|=

|AO|2(|BO|+|OC|)+|OC|2·|BO|+

|BO|2·|OC|=

|AO|2·|BC|+|BC|·|BO|·|OC|,

移项得

|AB|2·|OC|+|AC|2·|BO|-|AO|2·|BC|=

|BC|·|BO|·|OC|.

特别地，当点O是底边BC的中点时，易得下面的推论.

推论点O是△ABC底边BC的中点，则

|AB|2+|AC|2=2|AO|2+2|BO|2.

2推论的移植

由推论的结构特征，容易联想到将其移植到椭圆、双曲线中又会有怎样的结论呢？笔者经过探索得到了下面有趣的结论.

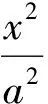
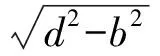
(2)∠F1AF2为锐角⟺dgt;c,且d≠a；∠F1AF2为钝角⟺dlt;c；∠F1AF2为直角⟺d=c.

图2

证明(1)如图2，由题设条件和推论得

(1)

其中c为椭圆的半焦距.又由椭圆的定义知

联立式(1)，式(2)得

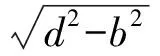
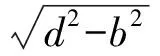
r1r2=a2+b2-d2.

∠F1AF2为锐角⟺dgt;c,且d≠a；

同理可证

∠F1AF2为钝角⟺dlt;c；

∠F1AF2为直角⟺d=c.

(3)在△F1AF2中，由余弦定理得

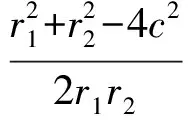
从而

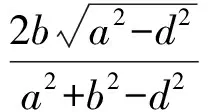
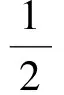
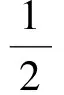
故性质1成立.

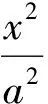
(2)∠F1AF2为锐角⟺dgt;c；∠F1AF2为钝角⟺dlt;c且d≠a；∠F1AF2为直角⟺d=c.

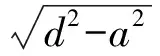
证明过程同性质1，限于篇幅本文略.

3性质的应用

推论及2个性质的应用很广泛，本文列举几例说明之.

(2000年全国数学高考试题)

(1)

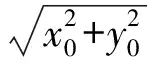
(2)

将式(1)变形代入式(2)化简得

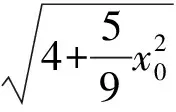
由性质1得

∠F1AF2为钝角⟺dlt;c.

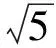
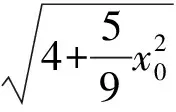
即

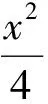
(2010年江西省数学高考试题)

(3)

由性质2知

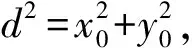
r2=2x0,

(4)

由式(3)，式(4)得

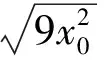
因为x0gt;0，所以

x0=2.

( )

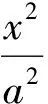
(2007年全国数学高考试题)

解由性质2得∠F1AF2=90°,从而

又由|AF1|=3|AF2|，得

解得

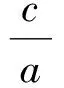
例4设F1,F2分别是椭圆x2+4y2=4的左、右焦点.

(2)略.

(2007年四川省数学高考试题)

解(1)因为

r1r2·cos∠F1AF2,

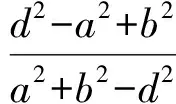
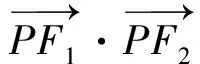
可见，用性质1和性质2求解与椭圆、双曲线焦点有关的问题还是较简便的，教学中只要潜心钻研、探索，就会有所收获.

[1] 朱德祥.初等几何研究[M].北京:高等教育出版社，1991.