一道易错概率题的课堂探究案例

●

(慈溪中学 浙江慈溪 315300)

一道易错概率题的课堂探究案例

●孙波英

(慈溪中学 浙江慈溪 315300)

在平时的例题教学中,经常会遇到这样的情景：看似正确的方法却得到错误的结果．其实,这种“偶然”通常隐藏着深层次的原因．在教学中,若能因势利导，鼓励学生发现问题、积极探究，则会取得意想不到的效果，使例题教学中蕴含的宝贵资源得到更有效的利用和挖掘．

下面记录了笔者在高三第一轮概率复习课上的一个片段及反思．有这么一道例题：

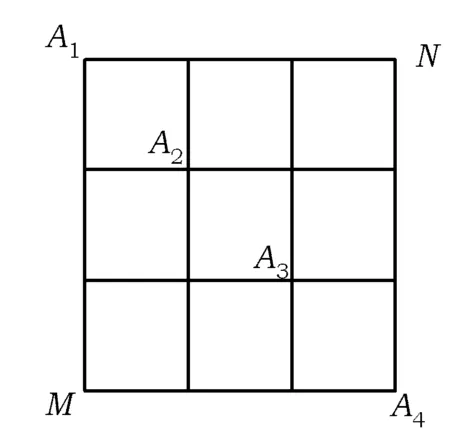
图1

例1如图1，在某城市中，M，N两地之间有整齐的方格形道路网，其中A1，A2，A3，A4是道路网中位于一条对角线上的4个交汇处．今在道路网M，N处的两人分别要到N，M处，他们分别随机选择一条沿街的最短路径，以相同的速度同时出发，直到到达N，M处为止．求甲、乙两人在A2处相遇的概率．

1课堂实录

按照惯例，题目给出后，先让学生思考几分钟，然后回答．

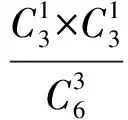
T：2种方法得到了2个截然不同的答案，到底谁错了呢？

S1：老师，我错了．

T：为什么？

S1：因为我没有让甲、乙把路走完，只考虑到相遇为止.其实他们是要走完的，因为条件中说“直到到达N，M处为止”．

下面有很多学生在点头，表示犯了同样的错误．

T：审题一定要仔细，审题可是解题的第一环节，以后不能这么粗心……

笔者话还没讲完，又有一位同学要求发言．

S3：我是让甲、乙相遇后继续走直到到达N，M处为止的，但是答案和S1是一样的．

T：说来听听．

S3：将它看成高尔顿板模型．记事件A：“甲从M出发，走6步经过A2到达N”,记事件B：“甲走3步从M到达A2”，记事件C：“甲继续走3步从A2到达N”．因为甲在每个路口都有往上和往右2种选择(A1N与A4N边上的路口只有一种选择)，所以和S1一样，从A2出发走3步.因为只能往上或往右，所以只能到达N，于是P(C)=1，故

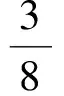
此时教室里寂静无声，大家都陷入了沉思．这种情况教师在课前没有考虑，一下子无法给出答案.权衡利弊后决定按照一贯的做法，降低难度后再将问题抛给学生．

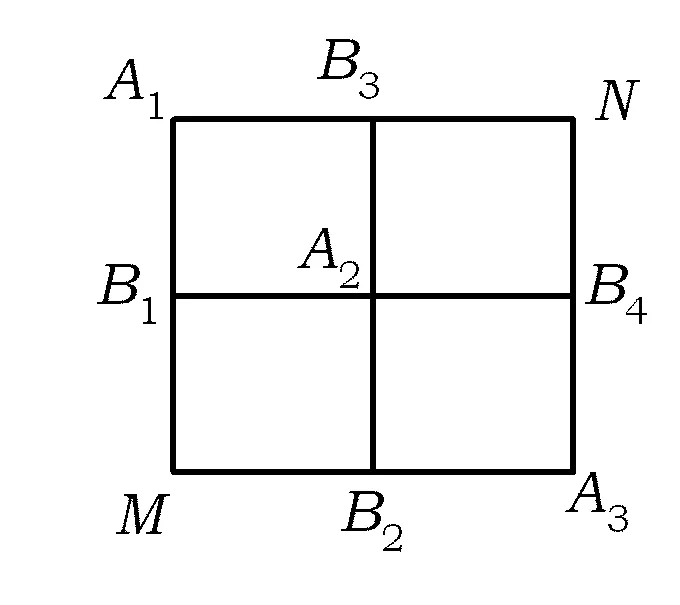
图2

T：当一下子无法看清原问题时，常用的办法是降低原题的难度，把它简化成2×2的方格怎么样？其他条件与原题相同，求甲从M出发经过A2到达N的概率．

大家都低头演算起来，几分钟后有学生举手.

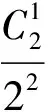
T：那么到底谁对呢？

S4：S2对！

T：为什么？

S4：因为甲从M到N共有以下6条路可走：

M—B1—A1—B3—N，M—B1—A2—B3—N;

M—B1—A2—B4—N;M—B2—A2—B3—N;

M—B2—A2—B4—N;M—B2—A3—B4—N．

其中有4条是经过A2的.因为条件中说“他们分别随机选择一条沿街的最短路径”，所以这6条路对于甲来说是等可能的.由古典概型的计算公式可得

因此S2是对的．

T：那么S3又错在哪里呢？

S4：按照S3的做法，甲所走的6条路径是不等可能的：

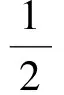
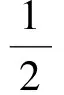
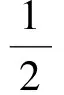
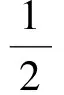
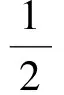
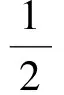
全体学生：哦，原来如此！

T：错解到底错在哪里？不是“有没有走完”的问题，而是“什么是等可能的”的问题．因为甲随机选择的是6条路，所以走每条路是等可能的，那么每个路口的选择是不等可能的.如果每次路口的选择是等可能的，那么走每条路就不等可能了．我们一定要很好的理解题设条件“他们分别随机选择一条沿街的最短路径”，才能找到它的概率模型，从而使问题迎刃而解．

2几点反思

2.1 重视审题能力的培养

审题是解题的第一环节，准确理解题意是正确解题的关键．学生在看到“他们分别随机选择一条沿街的最短路径”时，理解为甲在每个路口只有向上和向右2种选择(边A1N与A4N边上的路口只有一种选择)，而且只要有2种选择，这2种是等可能的，这才借用高尔顿板模型来解题，将“随机选择一条最短路径”与“他们分别随机从点M，N走到N，M，不走回头路”等同起来，这是造成错解的根本原因．

审题不单单是一种习惯，更是一种能力，绝不是考试前强调一下就能解决的问题,需要我们在例题教学中慢慢培养．教师除了要帮助学生构建数学知识体系，渗透数学思想方法，更应该教会学生如何审题．

教师在出示题目后，让学生有自主阅读的时间、鉴别信息真伪的空间、组合信息的平台和自主决定解题思路的机会，也让学生有“试误”的机会和勇气，并指导学生归纳总结，形成审题的规律和基本方法．

2.2 重视“错误资源”的有效利用

如何处理学生发生的错误越来越被人们所重视．对于学生发生的错误熟视无睹，只拿出正确的答案告诉学生就了事的做法定会遭到批判．然而仅仅指出学生的错误，不深入分析错误产生的根源同样也是不可取的．S1在看到S2的解法后，马上发现自己错了，错误的原因是没有让甲、乙把路走完．当时如果没有S3站起来，也许真的会将错因归结为审题不仔细，这个问题就这样过去了．

在例题教学中，通过学生的错误，分析探究错误产生的根源，引导学生不断反思，改善认知结构中不完善的地方，促使学生对已完成的思维过程进行周密且有批判性的再思考．