六类类比在数学解题中的应用

●

(杨贤江中学 浙江慈溪 315300)

六类类比在数学解题中的应用

●胡徐波张示达

(杨贤江中学 浙江慈溪 315300)

著名数学家波利亚曾指出：“类比是某种类型的相似性，是一种更确定的和更概念性的相似”.类比是从已经解决的问题和已经获得的知识出发，提出新问题和作出新发现的一个重要源泉，是一种较高层次的信息迁移，它是由特殊到特殊的推理．

类比推理的前提是2类对象之间具有某些可以清楚定义的类似特征、明确的类比关系，因此运用类比的关键是确定类比对象.而确定类比对象的基本原则是根据当前问题的需要，选择适当的类比对象．不能让类比仅仅停留在叙述方法或结构形式等外层表象上，还需要对数学结论的运算变形、思想方法、思维策略、推理过程等寻求内在关联，开展多角度、全方位的类比探析活动．由于类比推理的逻辑根据是不充分的，带有或然性，具有猜测性，不能作为一种严格的数学方法，因此还须经过严格的逻辑论证，才能确认其猜测结论的正确性．本文由问题出发，从定义生成类比、属性关系类比、降维减元类比、结构形式类比、思想方法类比、无限有限类比等6个不同角度，针对如何进行类比推理，作些分类探究解析的有益尝试，培养学生运用类比进行合情推理的能力．

1定义生成类比

问题1若定义集合A与B的运算：A⊗B={x|x∈A或x∈B,且x∉A∩B},试写出(A⊗B)⊗A成立的等式．

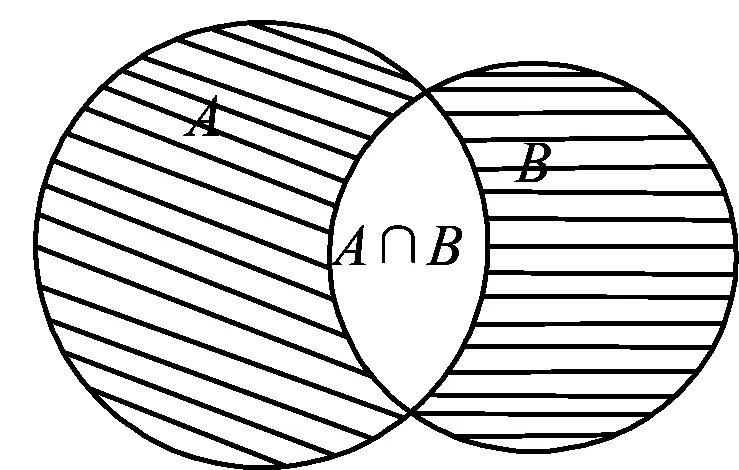
图1

探究这是一道抽象的集合问题，利用已有的集合知识，借助韦恩图，通过类比问题进行探索，可发现一些含有新定义集合运算关系的等式．若记A⊗B=C，如图1中阴影部分所示，则类比得

C⊗A={x|x∈C或x∈A,且x∉C∩A}=B,

因此

(A⊗B)⊗A=B．

问题2试指出三角形在空间的类比.

探究(1)由数目最少的简单分界元素所围成的几何图形来说:在平面上，2条直线不能围成一个有限的封闭图形，然而3条直线可以围成一个三角形；在空间里,3个平面不能围成一个有限的封闭几何体，然而4个平面可以围成一个四面体．因此，四面体可以看成三角形在空间中的类比．例如,由三角形的3条内角平分线相交于一点是三角形内切圆的圆心，即生成内心.可类比猜测：四面体的6个内二面角的平分面也相交于一点，而且这就是四面体内切球的球心，不妨也称之为生成内心(如图2).

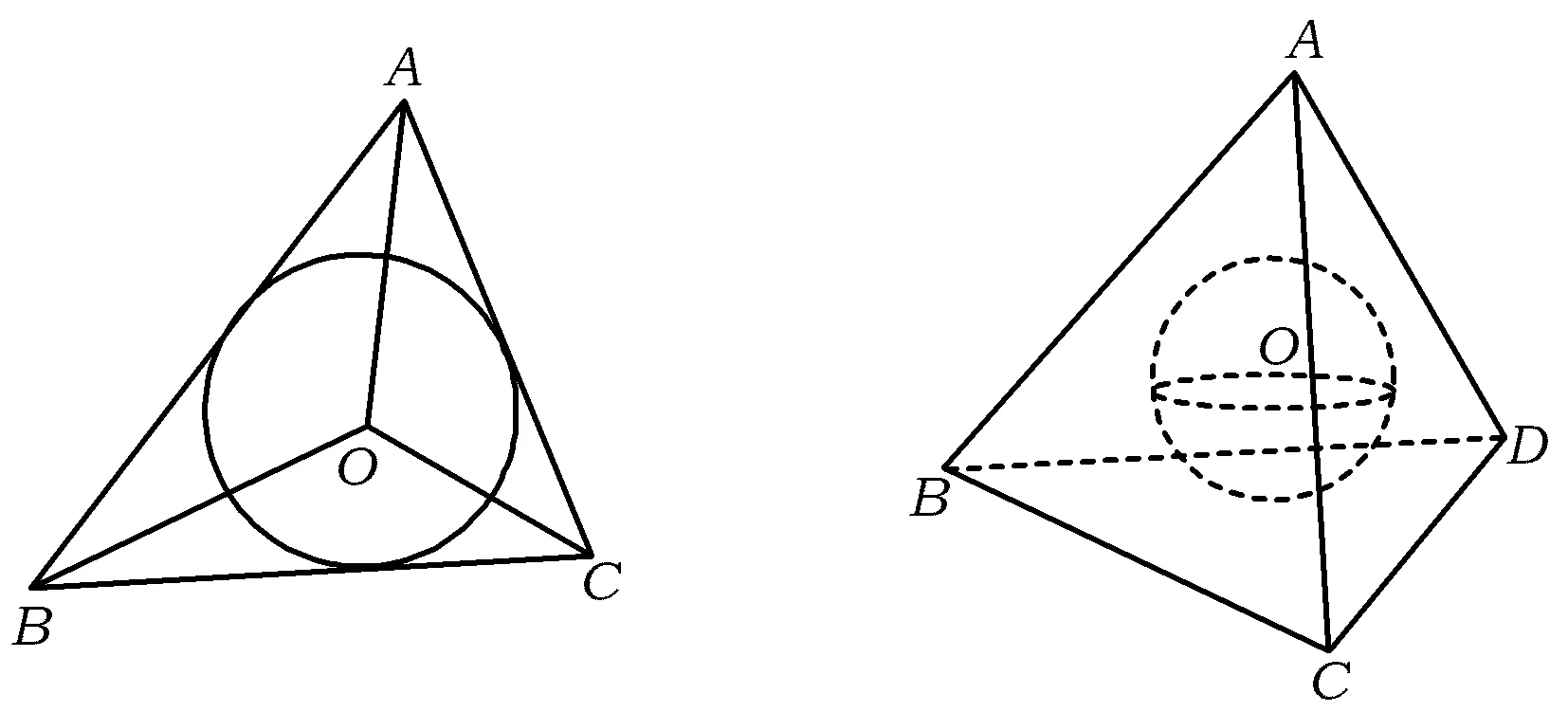
图2

(2)从直接生成的角度考虑:棱锥可以看成三角形在空间的类比，如果三角形可以看成将线段(所在直线)外的一点与线段上的各点用线段相连所生成的平面图形，那么棱锥就可以看成将多边形(所在平面)外的一点与多边形上各点用线段相连所生成的空间图形(如图3)．

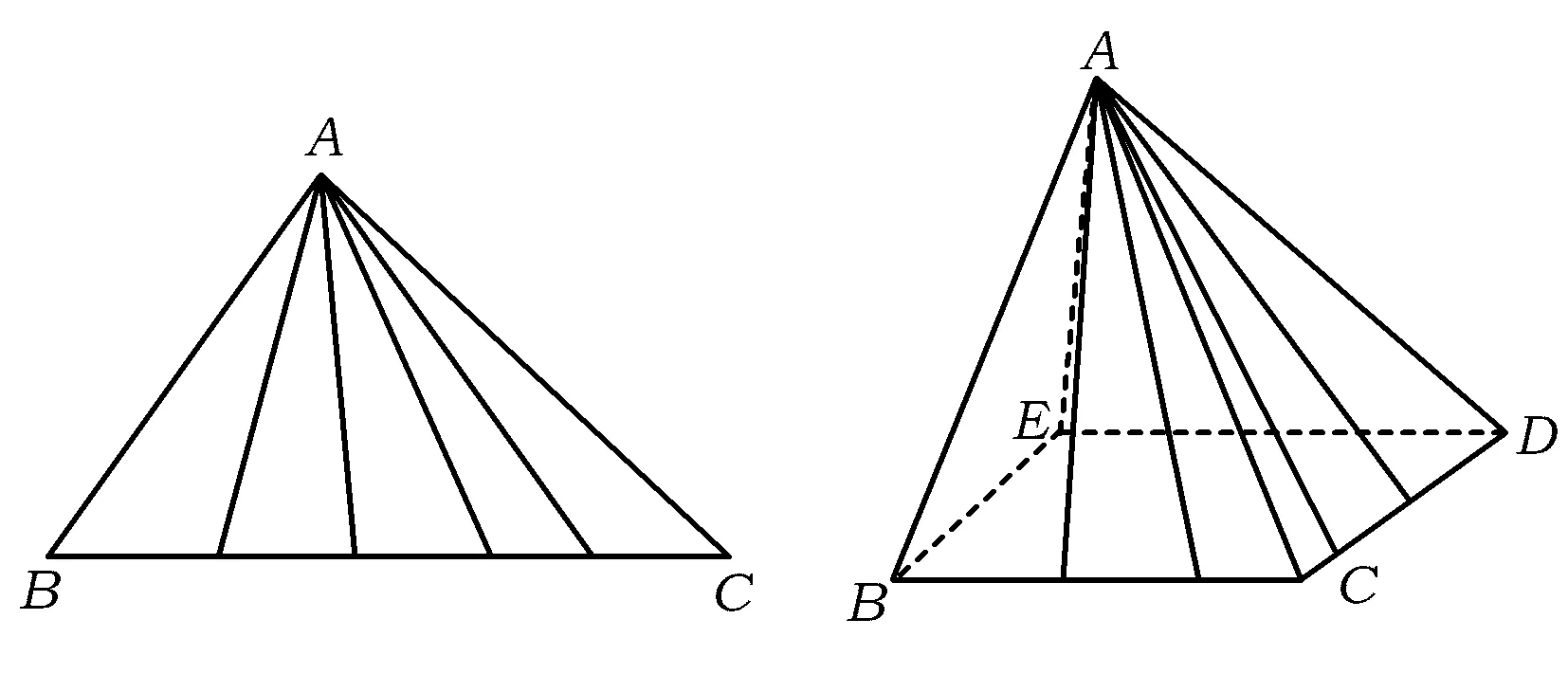
图3

2属性关系类比

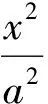
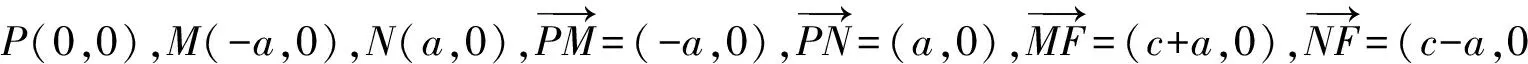
其中c2-a2=b2,于是

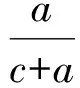
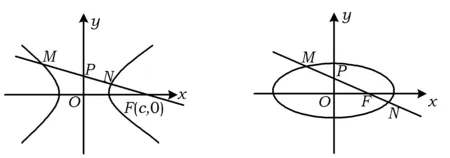
图4 图5

由于椭圆与双曲线有很多类似的属性关系，因此可类比双曲线的这一结论以及获得的这个定值的特殊方法，寻找其中变与不变的规律．同理，对于椭圆也可得

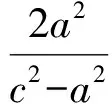
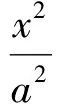
设此直线方程为y=k(x-c)(斜率k存在)，则点P(0,-kc)．设点M(x1,y1),N(x2,y2)，得

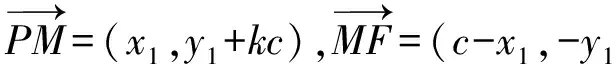
解得

同理可得

于是

(1)

(a2k2+b2)x2-2a2k2cx+a2k2c2-a2b2=0.

当Δgt;0时，由韦达定理得

代入式(1)得

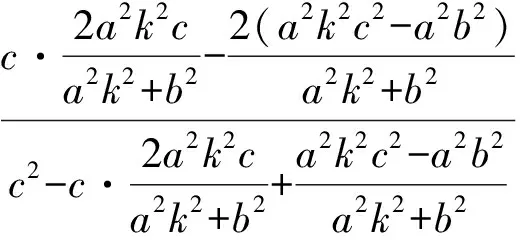
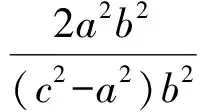
结论得证．

3降维减元类比

问题4如图6,在四面体ABCD内部有一点O，使得AO，BO，CO，DO与四面体的4个面BCD，CDA，DAB，ABC分别交于点A1,B1,C1,D1，且满足

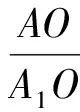
试求k的可能取值．

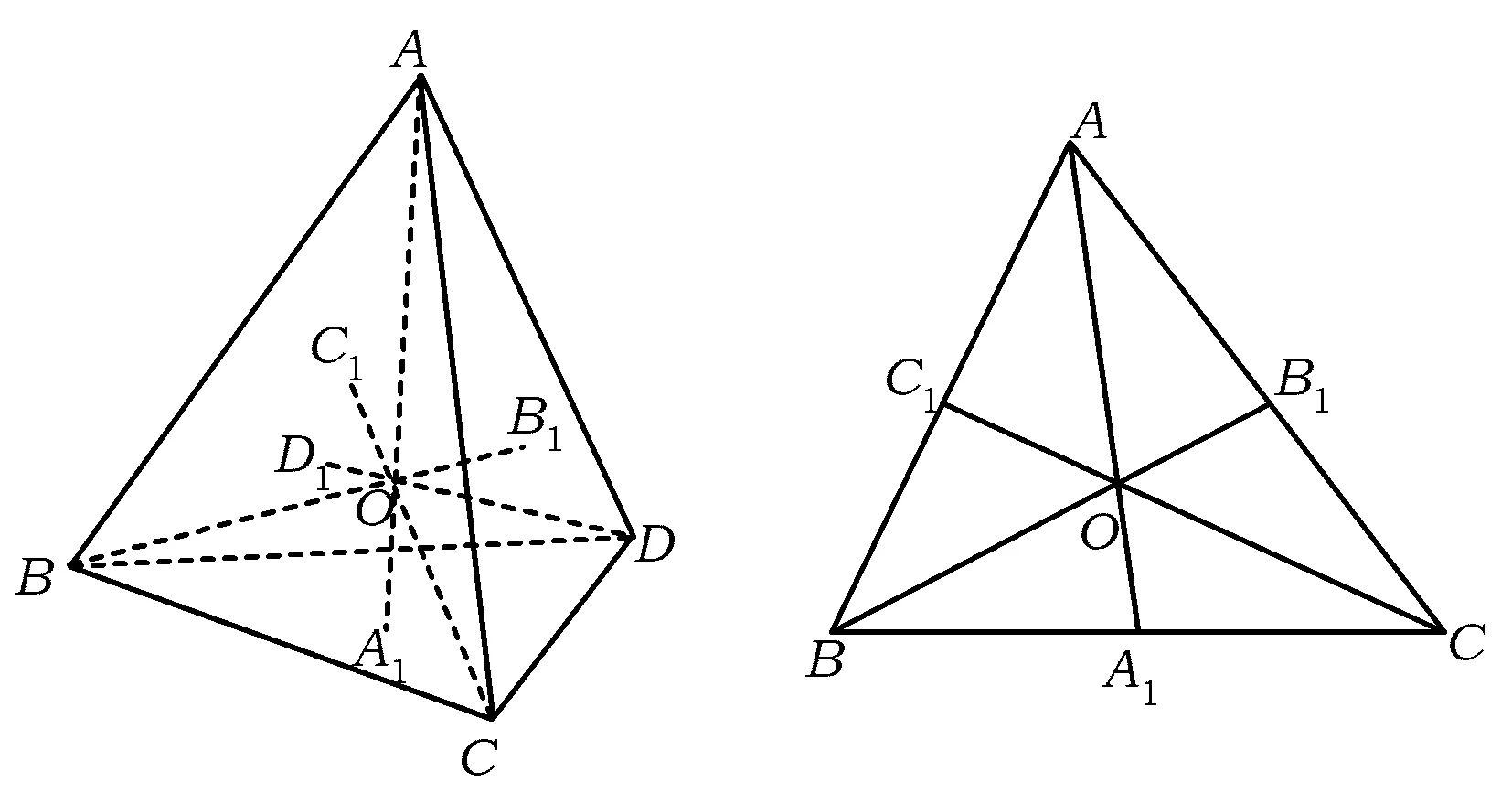
图6 图7

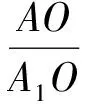
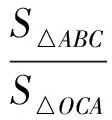
于是 3S△ABC=(k+1)(S△OBC+S△OCA+S△OAB),

解得

3=k+1，

故

k=2．

根据上述利用面积关系求解思路推理的启发，在空间四面体中，可转化为利用体积关系进行类比推理．在四面体中，因为同底四面体的体积比为对应的高之比，等于相似比，所以

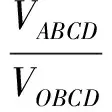
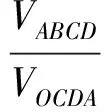
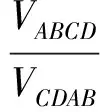
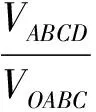
于是

4VABCD=(k+1)(VOBCD+VOCDA+VCDAB+VOABC)，

得

4=k+1，

故

k=3．

4结构形式类比

问题5任给7个实数xk(k=1,2,3,…,7),能否求证其中有2个实数xi，xj,满足不等式

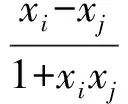
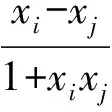
5思想方法类比

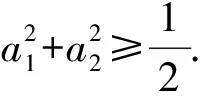
证明构造函数f(x)=(x-a1)2+(x-a2)2．因为对一切x∈R，恒有f(x)≥0，即

对一切x∈R恒成立,所以

从而

现若a1,a2,…,an∈R，a1+a2+…+an=1，请写出上述结论的推广，并加以证明．

探究由于函数与不等式有着深刻的内在联系，因此研究不等式通常需用函数的性质作为工具．已知这个不等式的证法是构造函数，利用二次函数的性质并结合判别式，实现函数与不等式的转化思想.现在只是从二元(a1,a2)推广到n元(a1,a2,…,an)的情形，因此结论的推广和证明完全可以类比上述构造二次函数，与不等式转化的思想方法获得解决．

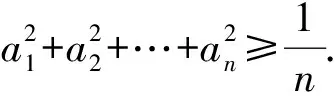
证明构造函数

f(x)=(x-a1)2+(x-a2)2+…+(x-an)2=

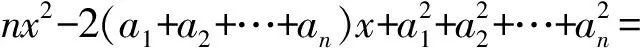
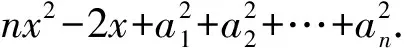
因为对一切x∈R，恒有f(x)≥0，所以

从而

6无限有限类比

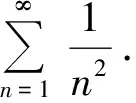
探究在不能运用极限方法求无限和时，可以通过无限和与有限和进行类比，寻找求解思路.设2n次代数方程

a0-a1x2+a2x4-…+(-1)nanx2n=0

(2)

有2n个不同的根c1,-c1,c2,-c2,…,cn,-cn，则

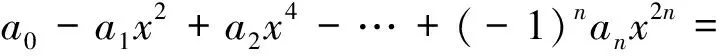
(3)

已知函数sinx的展开式

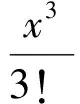
且方程sinx=0有无穷多个根为0,±π,±2π,±3π，…，它们也是无穷次方程

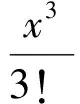
的根，则方程

(4)

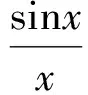
所以

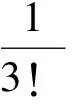
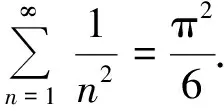
由于这一结论建立在无限与有限类比之上，因此它只是一个大胆的猜想，为了验证这一猜想的可靠性，可以运用复数的棣莫佛定理给予严格证明(限于篇幅，证明从略)．

总之，形神兼备的类比，其基本模式是：若对象A具有属性a，b，c，d，且对象B具有属性a，b，c，猜想：对象B具有属性d.类比推理的过程是从特殊到特殊、由此及彼的,具有猜测和发现创造结论、探究和提供思路、指引方向的巨大作用.教师引导学生自主类比，防止以表掩质的“乱比”，应突显学生的主体地位，让学生在直觉感知的基础上，自觉地形成探究问题的意识，充分锻炼发散性思维和发现创造性思维的能力，开拓新领域，逐步完善和构建合理有效的数学认知结构，真切地感悟形同神似的神奇类比．

[1] 波利亚.数学与猜想[M].北京:科学出版社，1984．

[2] 郑毓信.数学方法论[M].南宁:广西教育出版社，1996．