关于交流电机中“二相对称”概念的分析

江春冬，贾海朋，杜太行，安 东

(河北工业大学，天津300130)

0 引 言

交流旋转电机实现机电能量转换的介质是由旋转磁动势在气隙中产生的旋转磁场。三相电机由于绕组间的磁链彼此互相耦合，使得三相电机的动态数学模型复杂，它是一个高阶、非线性、强耦合的多变量系统，控制困难，使用不方便。为了使用电机的动态数学模型，就需要对数学模型进行化简，化简的基本方法就是坐标变换。

坐标变换只是从数学上对电机模型进行简化，不能改变电机的本质。简化时就要保证变化前后旋转磁动势是不变的，也就是等效的。这样，如何用简单的方法产生等效的旋转磁动势成了化简时要考虑的问题。分析三相交流电机磁动势时我们得到过这样的一个结论，即m(m≥2)相对称绕组中通入m相对称电流后，形成的基波合成磁动势是旋转磁动势。m相可以是二相、三相、四相……，其中以二相最为简单。

三相对称绕组是匝数相同、空间互差120°的绕组;三相对称电流是幅值相同、时间上互差120°的电流。四相及以上的对称绕组是匝数相同、空间互差360°/m角度的绕组，对称电流是幅值相同、时间上互差360°/m角度的电流。“二相对称”如果按照前面定义，应该互差180°，可二相对称绕组和二相对称电流分别在空间和时间上相差90°，为什么是这样的呢?

1 三相基波合成旋转磁动势分析

为了分析交流电机中“二相对称”所差角度问题，我们先将三相基波合成旋转磁动势的分析理论列写如下。三相对称电流的表达式:

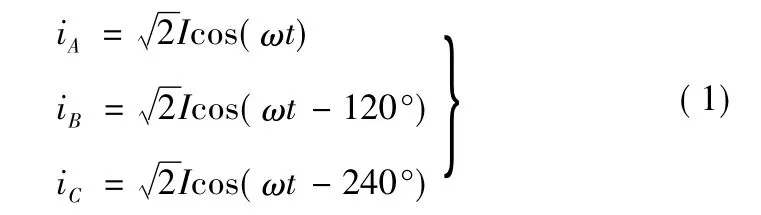
式中:I为电流有效值;ω为电流的角频率，ω=2πf1;f1为电流的频率。

在了解单相对称绕组通入单相交流电后产生脉振磁动势性质的基础上，选择A相绕组的轴线为空间坐标的原点，正相序方向为空间坐标x的正方向，同时选择A相电流达到最大值时为时间的起点，如式(1)，则A、B、C三相对称绕组通入三相对称交流电后，三个相产生的基波磁动势的表达式:

式中:Fφ1为各个单相脉振磁动势基波的幅值;τ为极距;为空间距离原点的电角度。

利用三角函数积化和差的公式将式(2)中的每一个式子进行展开，有:

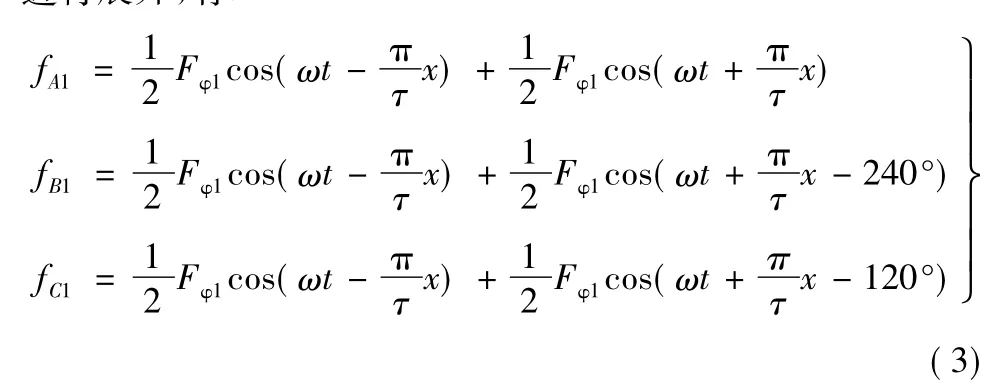
将fA1、fB1、fC1相加，式子右侧第二项的代数和由于对称而为零，则三个绕组的基波合成磁动势:

2 二相基波合成旋转磁动势分析

用同样的理论可以分析二相对称绕组通入二相对称交流电时产生的基波合成磁动势，此时，“二相对称”的概念就会清楚，角度上是互差180°呢还是互差90°?

(1)互差90°的二相基波合成磁动势分析

此时，二相对称的交流电流表示成:

将这样的电流通入到匝数相同、空间角度互差90°的绕组中，得到二个相的基波磁动势的表达式:

对式(6)中的两式相加，并进行和差化积，有:

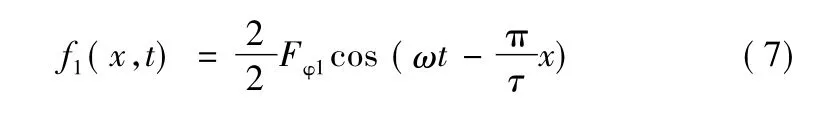
(2)互差180°的二相基波合成磁动势分析

此时，式(5)变成:

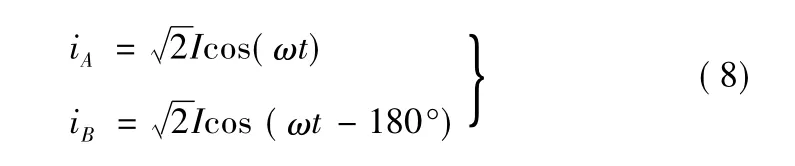
同样的，式(6)变成:

不用分解，将式(9)中的fA1和fB1相加，有:

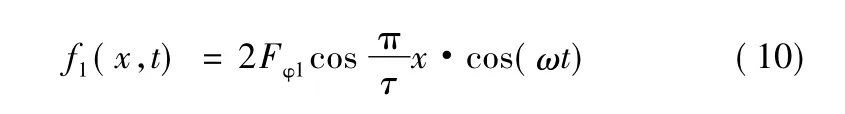
式(10)表示的基波合成磁动势为一个驻波，不是我们期望的行波，也就是旋转磁动势。

(3)二相合成基波旋转磁动势互差角度的物理解释

上述情况也可以从物理上来解释。如果二相对称绕组在空间互差的角度为180°，从感性上理解可认为这是绕在同一铁心上的二套紧密耦合的绕组，此时二套绕组的耦合系数为1。而且由于二套绕组匝数相同，这更象一台变比为1的变压器。在这样的二套绕组中再通入时间上互差180°的二相对称电流，任意瞬间，iA=-iB，合成磁动势F=NAiA-NBiB=2NAiA。这表明，各点处基波合成磁动势为随时间变化按电流变化规律而变化，这恰恰符合驻波的特点。

3 结 语

(1)若想产生期望的旋转磁动势，二相对称绕组需要是匝数相同、空间互差90°的绕组;二相对称电流需要是幅值相同、时间上互差90°的电流。这也正是三相异步电动机动态数学模型化简的基础。

(2)从空间或时间上互差的角度方面来看，二相对称和四相对称都是互差90°。但二相和四相相数不同，若绕组的匝数相同，交流电流的幅值相同，那么二相产生的基波合成旋转磁动势的幅值为Fφ1，四相的为2Fφ1。