直线电机振动抑制的载波移相策略研究

吴振兴 王逸林 王志伟 冀相

摘 要：PWM驱动电机系统中，在功率元件开关状态下会产生高频振动。针对变频驱动双三相直线电机会导致高频振动噪声的问题，提出使用载波移相技术降低噪声。首先根据电机高频振动与磁动势之间的关系，推导了互移30°的双三相直线电机磁动势的计算公式，经过分析得出结论：通过调节载波移相角改变电机两绕组电流中的高频谐波的角度差，能够有效地抵消电机合成磁动势的高频分量，降低了电机的径向电磁力和高频振动噪声，且载波移相角选取90°时整体抑制效果最好，并在MATLAB/Simulink环境下进行了仿真验证。最后基于RT-LAB软件搭建了全系统半实物实时仿真实验平台，对本文提出的控制策略及相关的分析进行了实验验证。

关键词：高频振动噪声;载波移相;直线电机;磁动势;实时仿真

DOI：10.15938/j.emc.2019.12.000

中图分类号：TM 359.4，TM 464文献标志碼：A文章编号：1007-449X（2019）12-0000-00

Abstract：In the PWM drive motor system， high frequency vibration occurs when the power element switches. Aiming at the problem of high frequency vibration and noise caused by frequency conversion driving multiphase linear motor， a carrier phase shifting technique is proposed to reduce noise. According to the relationship between the motor vibration and the magnetomotive force， the formula for calculating the MMF of a dual shift 30°multiphase linear motor is deduced. The conclusion is that the amplitude of the high frequency component of the motor synthesis magnetomotive force is effectively counteracted by adjusting the carrier shifted angle and the optimal phaseshifting angle is 90 degrees， which is carried out in the MATLAB/Simulink environment. The realtime simulation platform is built based on RTLAB software， the control strategy proposed in this paper and the related analysis and calculation is verified by experiments.

Keywords：high frequency vibration noise; carrier phase shifted; linear motor; magnetomotive force（MMF）; realtime simulation

0 引 言

现代电力驱动中，振动噪声越来越引起关注，在系统中电机振动必然会造成其输出质量的下降，对环境噪声有一定的影响及污染，而且高频的振动噪声对人体的影响更强烈[1-2]。降低电机振动噪声能保证人们正常健康的工作环境，特别在特殊情况下，如需求隐蔽航行的舰艇上，降低电机驱动时的高频振动噪声能有效保证其隐蔽性和安全性。

PWM逆变器供电时，定子绕组电流中必然含开关频率及其倍频边频带处的谐波分量[3-5]。文献[6]和[7]则分析了，由PWM引起的转矩脉动是电机振动和噪声的主要来源。这些高频谐波电流产生高频磁动势，导致电机高频振动噪声的产生。如果降低这些高频谐波电流，高频磁动势分量也会随之降低，从而降低由PWM 供电引入的高频振动噪声。

文献[3]中提出，通过调整2台逆变器载波之间相位角度，使得2台逆变器输出电流中相应边频带谐波相位角变化，削弱气隙磁动势中的对应频率谐波，达到降低电机高频振动目的。实际中为了抵消部分谐波等因素，双三相电机的2个绕组间空间上常采用互差30度的设计，即逆变器的参考波也需相应互差30°（下文称互移30°双三相直线电机），因此有必要针对载波移相调制技术进一步研究。

本文针对互移30°直线电机的高频振动噪声问题，推导了电机磁动势公式，分析了载波移相角的最优选取方案，并通过实验及仿真进行了验证90°为最优载波移相角。

1 电机高频振动与谐波磁动势的关系

在PWM逆变器供电电机系统中，逆变器开关器件的开通关断过程都会引发电机的振动噪声。文献[1]和[8]分析了PWM逆变器供电的电机电磁激振力及其振动噪声理论模型，提出感应电机的径向电磁力决定了电机的振动特性。

由表1可知，由于本文研究的直线电机系统中第二组逆变器（对应2Y绕组）的调制波滞后30°，与文献[3]中常规的载波移相技术得到的结论不同。常规的并联载波移相技术（即对于2组负载的调制波没有互差30°的系统）中，载波移相角为180°时，叠加电流能达到奇次倍（1、3、5等阶次）载波频率处完全抑制的效果，而载波移相角为90°只能达到2倍载波频段的谐波完全抑制的效果，对比下，一般都使用效果更好的移相角180°为系统的最优移相角。但对于本文研究的该电机系统中，载波移相角为180°时对各点没有抑制效果，且载波移相角为90°、270°等角度时的谐波抑制只能做到对应某几个谐波点的抑制，同时单从上表中还无法得知各载波移相角对整体谐波的抑制效果，还需要进行进一步深入分析和计算。

通过上图，可以发现，无论调制比多大，90°的谐波平方和都是最小的（由于移相角为90°和270°的对谐波抑制的整体效果一致，本章下文结论性叙述中均采用90°移相角）。故总体抑制效果都是最好的，且调制比越小，衰减抑制效果越明显。因此，可以判定90°为该系统的最佳移相角。

3 仿真分析

根据互移30°双三相直线电机系统模型进行载波移相调制技术的验证。直线电机部分使用M语言的S函数进行建模：输入量为2组角度互差30°的三相初级绕组电压、一组输入为0的三相次级绕组电压以及位置和速度信号，状态方程为同步旋转坐标系（dq坐标系）下磁链方程，输出量为2组初级绕组电流和一组次级绕组电流，以及力和能量。这里采集分析所用的2组A相电流就是从直线电机的S函数输出所得的两组初级绕组A相电流得到。

系统仿真参数：仿真步长设置为Ts=5 μs，模拟超级电容输出直流电压E=500 V，基波频率为10 Hz，开关频率设置4 kHz。调制比ma设置为1进行分析。仿真结果如图2～图6所示。

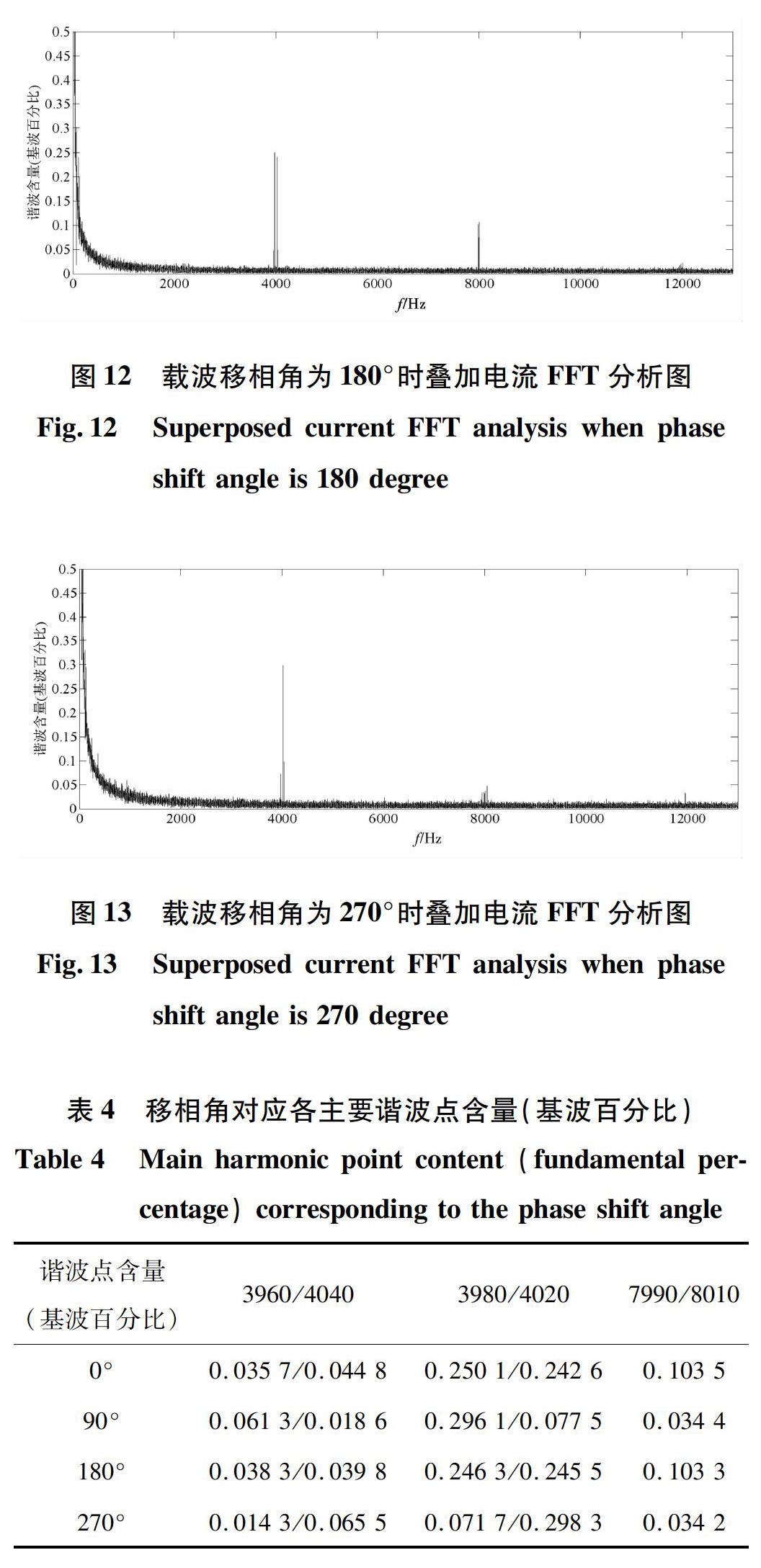
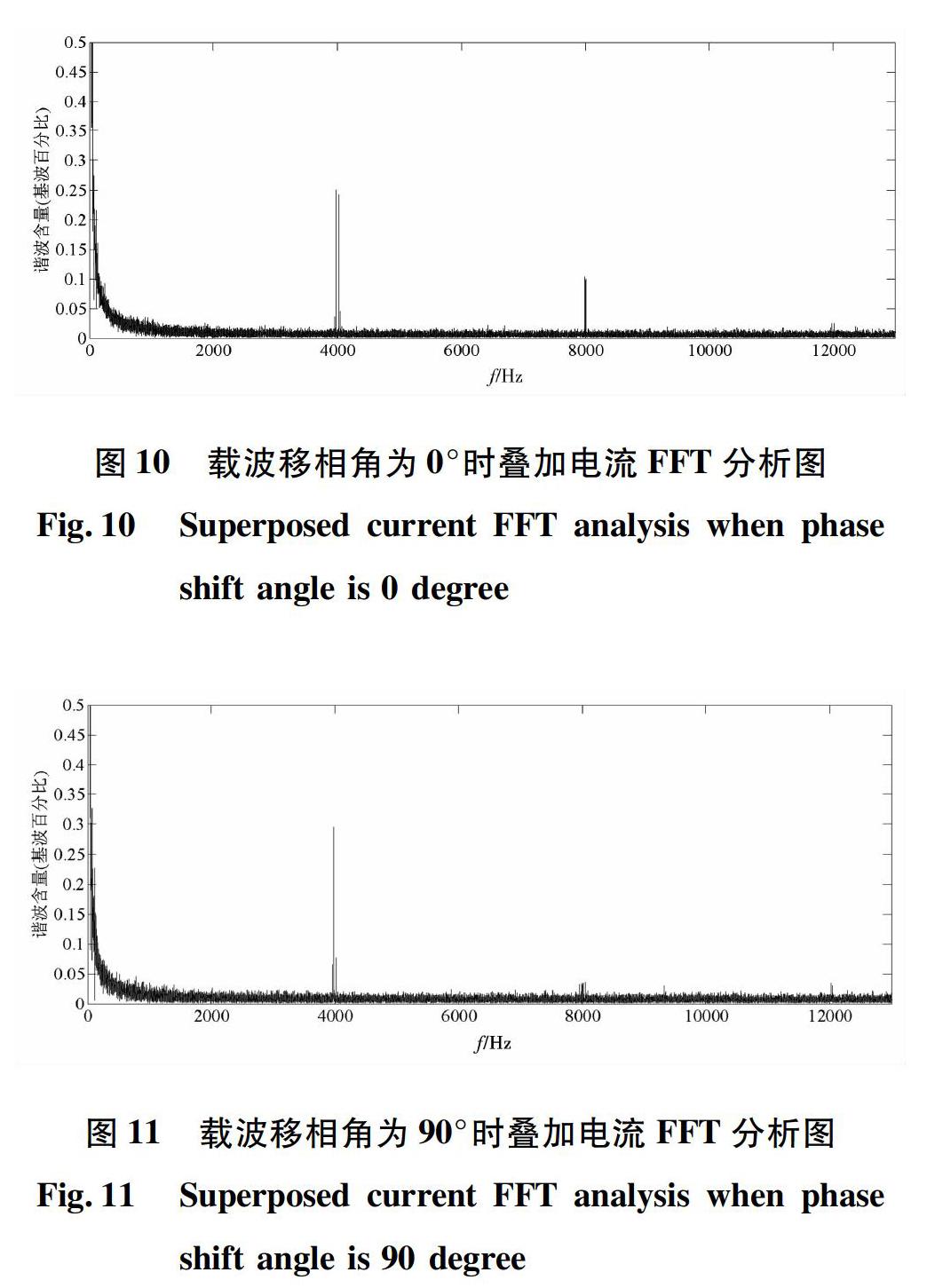
当载波移相角不同时，叠加电流的波形差异较小，为行文简洁，故直接给出FFT图。

考虑到载波移相对3倍及以上开关频率处谐波影响并不大，而且其谐波含量也较小，忽略不计，考虑到高频振动量级K∝∑I2kn，可以捕捉1～2倍开关频率处的主要谐波点进行平方和分析。

由表2数据可得，仿真数据分析：载波移相角选取为90°/270°时，对8 kHz处各点谐波基本抑制，抑制效果达到（1-0.025/0.096）=74%;载波移相角选取为90°时，对4 020和4 040 Hz谐波点基本抑制，抑制效果分别为（1-0.093/0.315）=71%和（1-0.003/0.010）=70%，载波移相角选取为270°时，对3 980和3 960 Hz谐波点基本抑制，抑制效果为分别为（1-0.094/0.315）=71%和（1-0.003/0.010）=70%，且载波移相角取180°时各点谐波基本无抑制作用。

又由表2可以算得，每个移相角对应的各谐波点含量的平方和如下表所示。

通过图表可以发现，载波移相角为180°时，谐波衰减抑制效果与0°时差别不大，载波移相角为90°时谐波抑制效果较好（由于90°/270°总体效果基本一致，下文叙述中均以90°为例）。经过上述判断，可以得到结论：载波移相角取90°时，不仅单个谐波点的抑制效果好，考虑到总振级效果（谐波含量平方和），90°得到的数值也更低，故此互移30°直线电机系统的降低振动噪声总振级的最优载波移相角为90°。

4 实验验证

实时仿真测试系统由图7所示，主要包括RTLAB实时仿真测试平台、底层控制器、控制器上位机组成，其中RTLAB实时仿真测试平台主要包括实时仿真上位机、OP5600仿真机及接口板。

按照图7的结构配置好本文所需的硬件设备，配置完成如图8所示。其中，从左至右介绍，左1（电脑）为逆变器控制器上位机，左2（显示器）为上位机软件调试显示设备，左3（3个控制盒）为数据IO转换器及相关设备，左4为逆变器控制器，右3为接口板卡箱，右2为OP5600仿真机及示波器，右1为实时仿真系统上位机。

移相角依次取为0°、90°、180°和270°，可以得到不同移相角下的2组定子A相叠加电流的示波器波形，并进行相关数据分析得到FFT分析图。

考虑到载波移相角不同时，叠加电流的波形看不出差别，为了行文简洁，不再给出其他载波移相角时的叠加电流波形。直接给出FFT分析图，如图10至图13所示。

使用FFT分析图提取出各主要谐波点含量，数据如下表4所示。

由表3数据可得，实验数据分析：载波移相角选取为90°/270°时，对8kHz处各点谐波基本抑制，对7 990和8 010 Hz谐波点的抑制效果达到（1-0.034 4/0.103 5）=68%;载波移相角选取为90°时，对4 020和4 040 Hz谐波点基本抑制，抑制效果分别为（1-0.077 5/0.242 6）=69%和（1-0.0186/0.044 8）=60%，载波移相角选取为270°时，对3 980和3 960 Hz谐波点基本抑制，抑制效果为分别为（1-0.071 7/0.250 1）=72%和（1-0.014 3/0.035 7）=60%。且载波移相角取180°时各点谐波基本无抑制作用。与仿真分析结论基本一致。

又由表4的数据可以算得，每个移相角对应的各谐波点含量的平方和如下表所示：

由表5可知，载波移相角为180°时，谐波衰减抑制效果与0°时差别不大，载波移相角为90°时，效果较好，抑制效果达到衰减（0.146 1-0.100 2）/0.146 1=31%。經过上述判断，可以得到结论：90°不仅单个谐波点的抑制效果好，考虑到总振级（谐波含量平方和）的比较，90°得到的数值也更低，故90°应为此互移30°直线电机系统减振降噪的最优载波移相角。

5 结 论

并联逆变器供电的电机系统中，由PWM调制会产生的高频谐波电流以及带来的电机高频振动，而通过载波移相策略，能抑制电机电流的高频谐波分量，从而降低了电机的合成谐波磁动势。通过理论推导和实验验证得到，在双三相互移30°的直线电机系统中，载波移相角选取90°时，能最有效地降低系统的高频谐波分量，从而降低电机的高频振动噪声。

参 考 文 献：

[1] Besnerais J L， Lanfranchi V， Hecquet M， et al. Prediction of audible magnetic noise radiated by adjustablespeed drive induction machines[J].IEEE Transactions on Industry Applications， 2010， 46（4）：1367.

[2] 顾立天. 永磁同步电机变频调速系统低噪声PWM技术研究[D]. 沈阳：沈阳工业大学， 2014.

[3] 袁飞雄， 黄声华， 郝清亮. 采用载波移相技术永磁电机高频振动抑制研究[J]. 电机与控制学报， 2014， 18（7）：12.

YUAN Feixiong， HUANG Shenghua， HE Qingliang. Vibration reduction control using carrier phase shifted for permanent magnet synchronous motor fed by bual PWM inverters[J]. Electric Machines and Control， 2014， 18（7）：12.

[4] 徐超， 高格， 刘辉，等. 载波移相逆变器并联系统环流分析与抑制[J]. 电力电子技术， 2014， 48（1）：74.

XU Chao，GAO Ge， LIU Hui，et al.Analysis and restrain of circulating current in carrier phaseshifted parallel inverters[J].Power Electronics， 2014， 48（1）：74.

[5] 王志. 基于三相四桥臂逆变器驱动的电机控制系统EMC研究[D].武汉：华中科技大学， 2008.

[6] Kimball J W， Zawodniok M. Reducing commonmode voltage in threephase sinetriangle PWM with interleaved carriers[J]. IEEE Transactions on Power Electronics， 2011， 26（8）：2229.

[7] LIANG W， WANG J， LUK C K， et al. Analytical modeling of current harmonic components in PMSM drive with voltagesource inverter by SVPWM technique[J]. IEEE Transactions on Energy Conversion， 2014， 29（3）：673.

[8] Hashemi N， Lisner R， Holmes D G. Acoustic noise reduction for an inverterfed threephase induction motor[C]// Industry Applications Conference， 2004. Ias Meeting. Conference Record of the. IEEE Xplore， 2004：2030-2035 vol.3.

[9] TRZYNADLOWSKI A M .Active attenuation of electromagnetic noise in an inverterfed automotive electric drive system[J]. IEEE Transactions on Power Electronics， 2006， 21（3）：693.

[10] TimárP. L. Noise and vibration of electrical machines[M]. Distribution for the U.S.A. and Canada， Elsevier Science Pub. Co， 1989.

（編辑：张 楠）