异步电动机的SVM－DTC控制

蒋建虎，姬宣德

(洛阳理工学院，河南洛阳471023)

0 引 言

直接转矩控制是异步电动机高性能的控制方法。文献［1］提出基本直接转矩控制(BASICDTC)的方案，但转矩脉动与磁链脉动一直制约着直接转矩控制系统的性能。文献［2］采用精细开关选择表减轻了转矩脉动和磁链脉动，但没有从根本上解决问题。本文采用空间电压矢量调制与直接转矩控制相结合(SVM-DTC)的方法，以减小转矩和磁链脉动，利用全阶磁链观测器观测定子磁链以提高观测精度，并提出一种单自由度极点配置方法实现磁链观测器的极点配置。仿真结果表明，系统不但实现了转矩和磁链的定量控制，降低了转矩脉动和磁链脉动，提高了定子磁链的观测精度，而且同时使得逆变器开关周期恒定，更易于数字化实现。

1 SVM－DTC基本原理

基本直接转矩控制的控制思想是:在保持定子磁链幅值恒定的情况下，一个控制周期内依据磁链和转矩误差的正或者负，通过查表的方式选择八个定子电压矢量中的一个来控制磁链和转矩增加或者减小的趋势。由于逆变器产生电压空间矢量的有限个数使得转矩和磁链不能同时得到最佳调节，基于这一控制策略的转矩脉动和磁链脉动必然较大。直接转矩控制对磁链和转矩的控制是一种“定性”的方法。为使转矩和磁链得到合理的调节控制，PWM逆变器就必须能够产生任意需要的电压空间矢量。与传统直接转矩控制不同，SVM-DTC对磁链和转矩的控制是一种“定量”的方法，在空间矢量模式下，具有逆变器开关周期恒定、减小转矩和磁链控制脉动的优点。SVM-DTC运用SVM生成变换器所需的参考电压矢量，这个参考电压矢量同时包含转矩控制与磁链控制的信息。

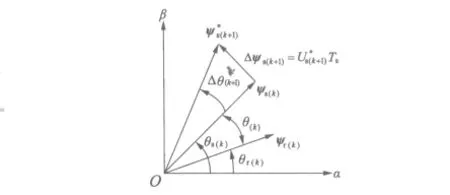
如图1所示，磁链矢量在复平面上逆时针旋转，θr为转子磁链与横轴α的夹角，θs为定子磁链与横轴α的夹角，θ(k)为第k拍定子磁链与转子磁链的夹角，即转矩角，代表着第k拍转矩的大小;ψs(k)为第k拍的定子磁链矢量为第k+1拍的控制目标定子磁链矢量，Δψs(k+1)为第k+1拍要求增加的定子磁链增量，这个增量由第k+1拍控制周期Ts的参考电压矢量来完成。显然的径向分量代表了磁链控制的需求，的切向分量代表了转矩控制的需求。因此，由图可以得到第k+1拍参考电压空间矢量的计算式:

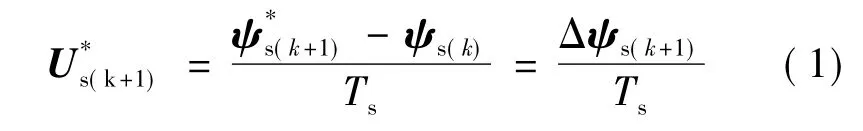
为精确起见，应考虑到定子电阻压降，在两相静止坐标系中，参考电压空间矢量:

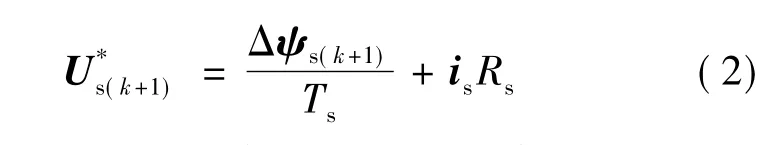
SVM-DTC利用转矩和磁链的偏差通过两个PI调节器，分别生成电压空间矢量的切向分量和径向分量，然后由SVM生成逆变器的开关信号，使得转矩和磁链脉动大大减少。与基本直接转矩控制不同，SVM-DTC不是用查表的方式来实现电压空间矢量的选择，而是根据切向分量和径向分量的要求实时生成任意幅值和任意方向的矢量，克服了基本直接转矩控制策略在一个控制周期中只发出有限幅值和有限方向的电压空间矢量。异步电动机SVM-DTC控制系统框图如图2所示。

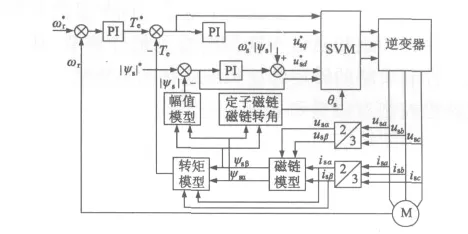
图2 异步电动机SVM-DTC控制系统框图

2 全阶磁链观测器

在两相静止参考系下，异步电动机可以用下列状态方程描述:

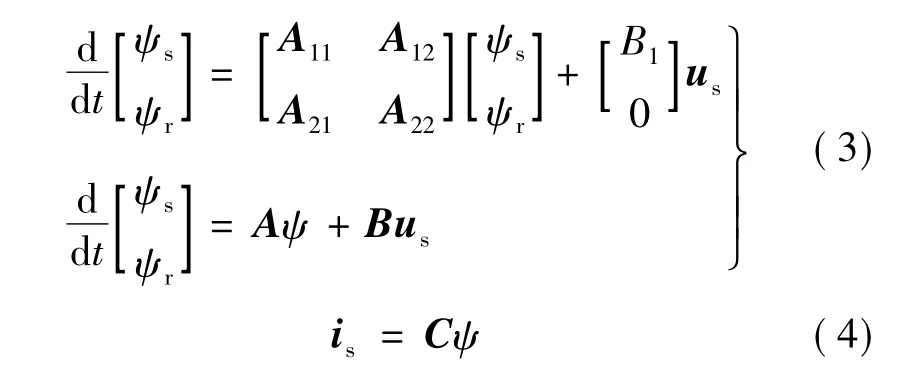
估计定子磁链和转子磁链的状态观测器可以通过下列方程描述:

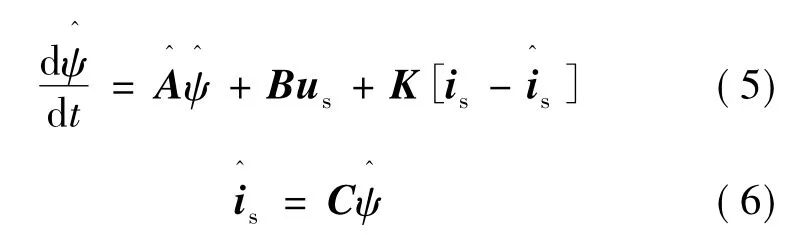
上述表达式中，“^”代表观测器的估计值。K是观测器增益矩阵。观测增益矩阵K可以表示为如下矩阵形式［6］:

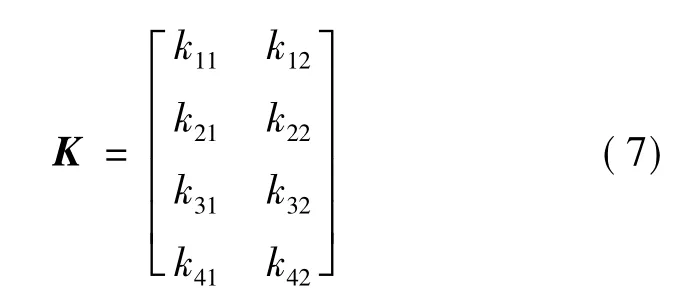
3 状态观测器极点配置方法

利用式(5)减去式(3)得到观测器误差方程:

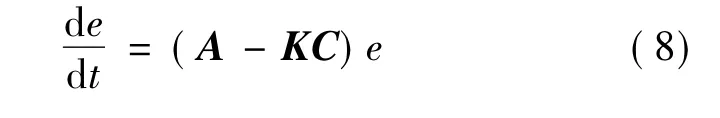
由式(8)可知，系统误差e的收敛速度取决于系统矩阵A-KC的极点位置［7-8］。如果所选矩阵A-KC的特征值使得误差向量的动态特性渐进稳定且足够快，则任意误差向量都将以足够快的速度收敛于零(原点)。误差向量e的收敛速度取决于系统矩阵A-KC的极点位置，通过增益矩阵K可以配置观测器需要的任意极点位置。

式(7)的增益矩阵K有八个位置参数，极点配置极为复杂，文献［9］把其参数缩减为四个，文献［10］进一步缩减为两个参数，增益矩阵K变为:

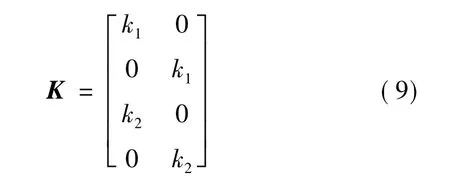
式(9)虽然解决了受电机参数和速度影响的限制，但是两个参数的自由度还是使极点配置极为不方便。为了方便快捷有效地配置观测器极点，本文提出一种新型配置方法，令式(9)中的参数绝对值相等，即:

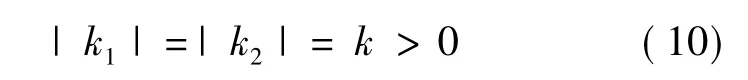
这样参数只有四种可能:k1=k，k2=-k;k1=k，k2=k;k1=-k，k2=k;k1=-k，k2=-k。利用MATLAB绘出当k在0至1之间的十个数值(递增量为0.1)时观测器的极点轨迹，速度从零变化到基速，如图3所示。

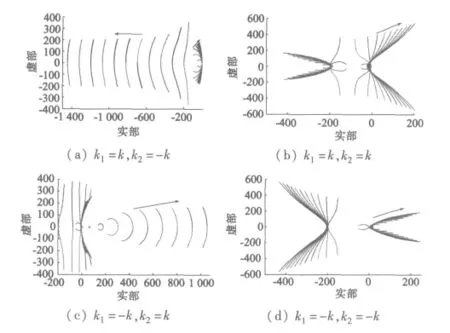
图3 四种情况下观测器极点的变化轨迹

由图中极点变化轨迹可知，随着k的增加，后三种情况中的一对极点实部变为正值，系统不稳定。增益矩阵K可以改变如下:

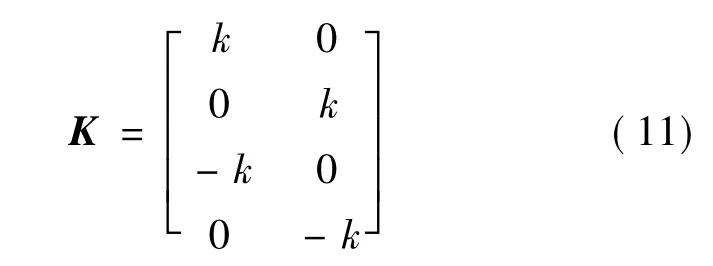
这样，增益矩阵只有一个参数，在新型配置方法情况下，极点配置更为方便快捷有效。

从图3可以看出，观测器的极点是共轭复极点，其对应分量是衰减振荡的。极点值的实部决定观测器的快速性，虚部与实部之比决定观测器的稳定性。从图4可以看出，当k从1增加到11(增量为1)时，左一对极点的实部随之增加，观测器收敛速度加快，而稳定性变差。为了同时满足观测器快速性和稳定性的要求，观测器极点实部的绝对值不能太大;右一对极点随之接近虚轴，实部仍然为负，保证了观测器稳定。

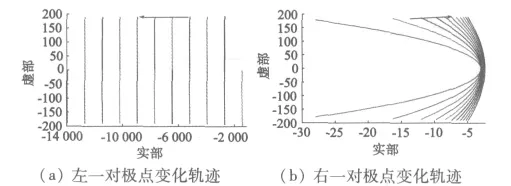
图4 k为正整数时观测器极点变化轨迹

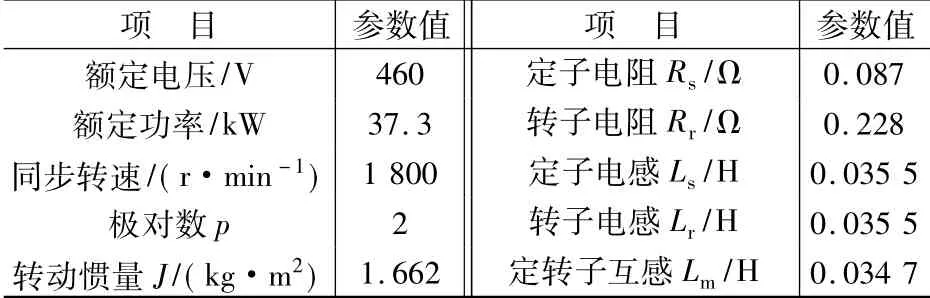
表1 异步电动机参数

4 仿真结果及分析

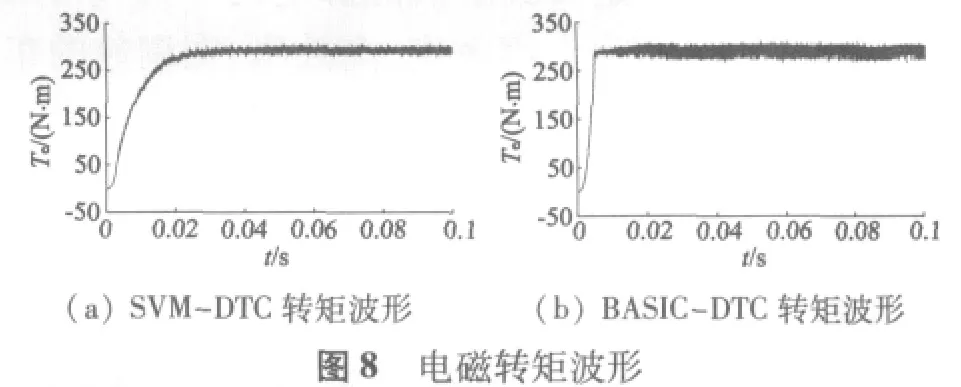
本文分别采用BASIC-DTC和SVM-DTC两种方案对异步电动机系统进行仿真，并作出相应的比较，两种方案均采用相同的电机参数，如表1所示。仿真结果如图5～图8所示。

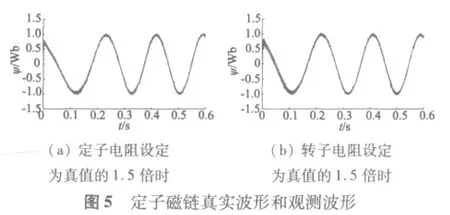
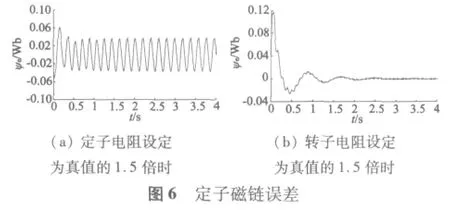
从图5(a)和图6(a)可以看出，在定子电阻参数变化情况下，定子观测磁链能够快速跟踪真实磁链，虽然幅值跟踪有误差(小于0.04)，但跟踪相位相同，这一点对于直接转矩控制系统尤为重要;从图5(b)和图6(b)可以看出，在转子电阻参数变化情况下，观测器也能实现磁链跟踪，而且稳态跟踪误差几乎为零，由此看出转子电阻参数变化对定子磁链稳态值几乎没有影响;由此看出，在单自由度极点配置方法下，全阶磁链观测器对定、转子参数变化具有很强的鲁棒性。从图7、图8可以看出，与BASICDTC方案相比，SVM-DTC方案电流波形更接近正弦波，转矩脉动减小，并使逆变器开关周期恒定，更易于数字化实现。

［1］ Depenbrock M.Direct self-control(DSC)of inverter-fed induction machine［J］.IEEE Trans.on Power Electronics，1988，3(4):420-429.

［2］ Casadei D，Serra G，Tani A.Implementation of adirect torque control algorithm for induction motors based on discrete space vector modulation［J］.IEEE Trans.on Industry Applications，2000，15(4):769-777.

［3］ Song Wen-xian，Yao Gan，Zhou Wen.Pole Arrangment Method of Full-OrderState Observer for Asynchronous Motor［J］.Motion Control and Apllication，2008，35(9):6-10.

［4］ Marchesoni M，Segarich P，Soressi E.A simple approach to flux and speed observation in induction motor drives.IEEE Trans.Industrial Electronics，1997，4(4):528-535.

［5］ Kojabadi H M，Chang L.Comparative study of pole placement method in adaptive flux observers［J］.Control Engineering Practice，2005，13(6):749-757.

［6］ 郑泽东，李永东，王琛琛.异步电机全阶自适应磁链观测和速度辨识研究［J］.电气传动，2006，36(7):7-10.

［7］ 奚国华，高宏洋，许为.定子磁链全阶观测器增益矩阵的确定方法［J］.中南大学学报，2008，39(4):793-798.

［8］ 黄文新，李勇，胡育文.用空间电压矢量调制异步电动机的直接转矩控制［J］，南京航空航天大学学报，2007，39(1):127-132.

［9］ 郎宝华，刘卫国，周熙炜.基于参考磁链空间电压矢量调制策略的PMSM-DTC系统［J］.电气传动，2007，37(7):21-25.

［10］ 张继勇，李新兵，束长宝.基于空间矢量无速度传感器感应电机的直接转矩控制［J］.机械电子工程，2005，22(3):22-25.