范德蒙行列式的应用探讨

张 毅

(长江大学信息与数学学院, 湖北 荆州 434023)

范德蒙行列式的应用探讨

张 毅

(长江大学信息与数学学院, 湖北 荆州 434023)

范德蒙行列式是《线性代数》的重要内容和研究工具，在许多方面有着广泛的应用。主要讨论了范德蒙行列式在证明问题中的应用。

范德蒙行列式；泰勒公式；克莱姆法则

在《线性代数》中，著名的范德蒙行列式[1]描述如下：

范德蒙行列式构造很独特、形式非常的优美，在线性代数理论的研究和应用中都非常重要。下面，笔者通过几个实例来说明范德蒙行列式在证明问题中的应用。

例1设x>y>z>0，试证明:

分析要证明题中的行列式的值小于0，而行列式是3阶的，所以自然会想到直接展开计算，但这样做会遇到多变量的高次多项式的因式分解问题，做起来比较繁琐，而这个3阶行列式的第1，2列的元素已具备范德蒙行列式的元素取值特点，故笔者考虑用范德蒙行列式的结论。

证明记：

故：

由已知x>y>z>0，有(y-x)<0,(z-x)<0,(z-y)<0，所以有f(x,y,z)<0。

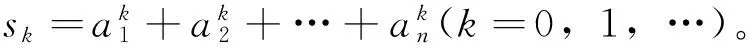
证明

因此：

例3证明：对平面上n个点(ai,bi)(1≤i≤n)(a1,a2,…,an互不相等)，必存在唯一的一个次数不超过的n-1的多项式f(x)通过该n个点(ai,bi)(1≤i≤n)，即f(ai)=bi(1≤i≤n)。

分析要证明n个等式成立，也就是要证明n个方程组成的方程组有解，很自然地会想到克莱姆法则，再根据系数行列式的特点，故考虑用范德蒙行列式的结论。

证明设f(x)=c1xn-1+c2xn-2+…+cn-1x+cn，要使f(ai)=bi(1≤i≤n)，即满足关于c1,…,cn的线性方程组：

而该方程组的系数行列式为范德蒙行列式：

当a1,a2,…,an互不相等时该行列式不为0，由Cramer定理知方程组有唯一解，即对平面上的n个点(ai,bi)(1≤i≤n)(a1,a2,…,an互不相等)，必存在唯一的一个次数不超过的n-1的多项式f(x)通过该n个点。

例4设f(x)在区间I上n阶可导(n≥2)，若对∀x∈I，|f(x)|≤M0,|f(n)(x)|≤Mn(M0,Mn为正常数)，证明:存在n-1个正常数M1，M2,…，Mn-1，使对∀x∈I，有|f(k)(x)|≤Mk(k=1，2，…，n-1)。

分析题中出现n阶导数，很自然地会想到泰勒公式[2]，要证明存在n-1个正常数，会想到建立方程组。

证明设a1,a2,…,an-1∈I，且ai≠0,ai≠aj(i≠j)，由泰勒公式，对于i=1，2，…，n-1，有：

由此得：

因此：

(1)

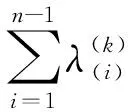
由此推得∀x∈I，∀k=1，2，…，n-1，有：

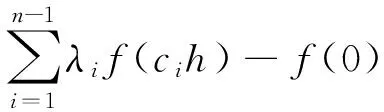
分析根据题意，按照高阶无穷小的定义，结合泰勒公式和克莱姆法则来证明此题。

证明由题设条件，可得f(cih)(i=1，2，…，n+1)在x=0处带有皮亚诺型余项的马克劳林展开式:

这是以λ1，λ2…,λn+1为未知数的线性方程组，其系数行列式为：

[1]北京大学数学系几何与代数教研室代数小组.高等代数[M].北京：高等教育出版社，1988.

[2]华东师范大学.数学分析[M].北京：高等教育出版社,2001.

[3]吴良森,毛羽辉.数学分析习题精解：多变量部分[M].北京：科学出版社，2005.

[编辑] 洪云飞

10.3969/j.issn.1673-1409.2011.08.004

O151.2

A

1673-1409(2011)08-0010-03