RC文氏桥振荡器稳幅环节的仿真研究

邹学玉

(长江大学电子信息学院， 湖北 荆州 434023)

RC文氏桥振荡器稳幅环节的仿真研究

邹学玉

(长江大学电子信息学院， 湖北 荆州 434023)

非对称RC文氏桥振荡器的稳幅环节直接影响到在整个频率调节范围内能否起振、并且能否获得较好的正弦波。采用电路稳定性分析方法，通过研究非理想条件下电路振荡条件，导出了理想条件下振荡电路的振荡频率和起振与平衡条件，设计了相应的稳幅环节，并采用Multisim对稳幅环节的设计进行仿真试验，仿真结果表明该计算方法是可行的，可以为非对称RC文氏桥振荡电路的设计提供参考。

文氏桥振荡器；振荡频率；起振条件；稳幅电路

在低频正弦波信号发生器电路中，文氏桥正弦波振荡电路结构简单，只要稳幅措施得当即可输出频率和幅度较为稳定的正弦波，由于其频率调节范围范围较大，并且具有桥式结构，从而在测量、自动控制、电子技术等领域有着广泛的应用[1]。RC文氏桥正弦波信号振荡电路通常划分为放大、选频、稳幅等基本环节[2]。在分析振荡电路的振荡频率、起振条件时均基于放大器为理想放大器，并且RC串并联网络中的R、C是严格对称相等的。在采用双联电位器频率调节时起振与平衡条件较为容易实现，但在实际应用中，当调节R改变频率使R逐渐变小时，电路振荡条件往往受电路参数非理想化因素影响而破坏，从而导致振荡器停振。尽管一些学者对RC文氏桥振荡电路展开了不同程度的研究，但基本上

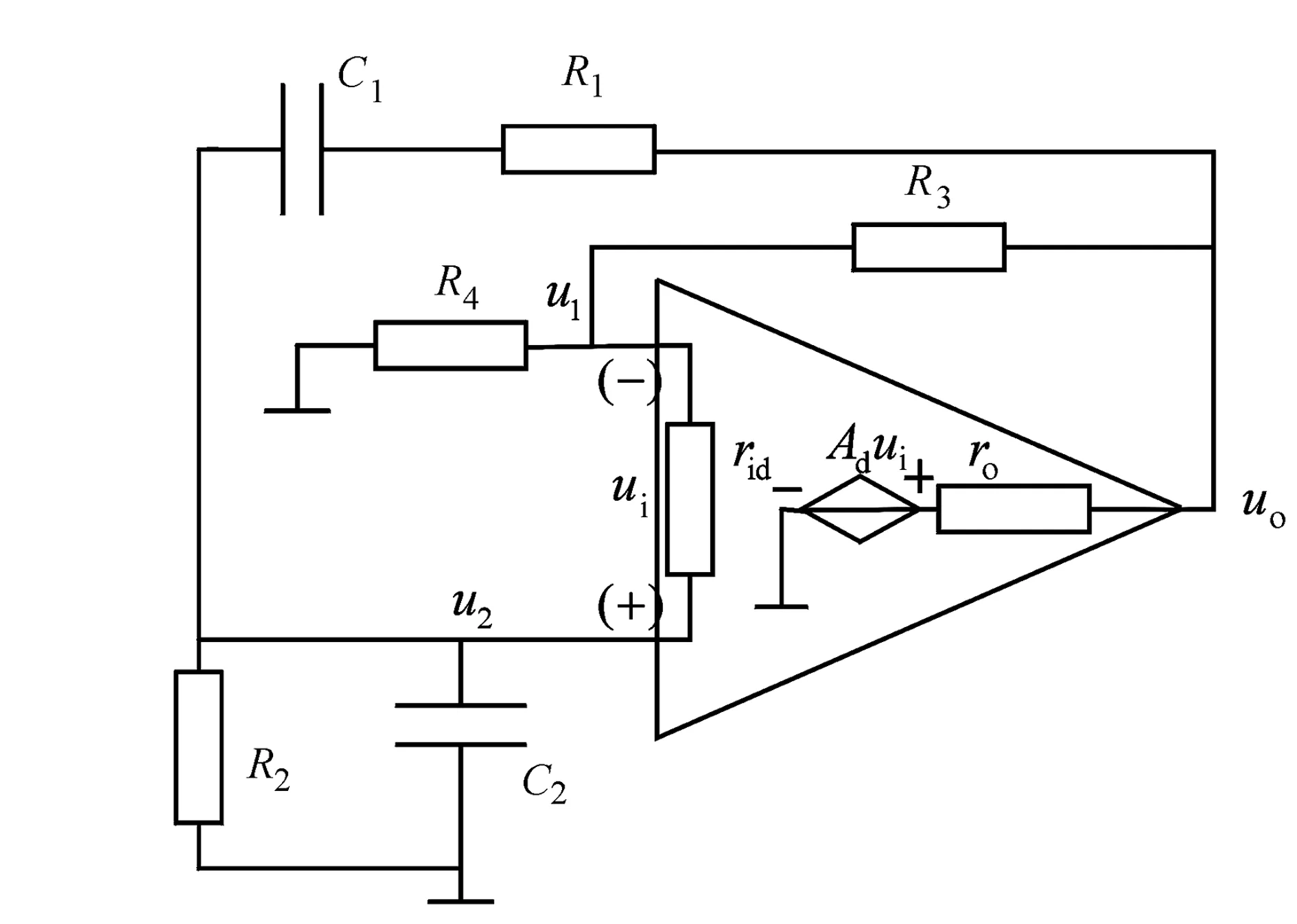
图1 RC文氏桥振荡电路等效电路图

是基于对称性结构条件下的振荡条件的研究[3-5]。为此，笔者将非对称的RC文氏桥振荡电路采用电路的基本分析方法进行分析研究，设计非对称RC文氏桥的稳幅环节，并采用Multisim对其进行仿真验证。

1 振荡条件分析

若考虑运算放大器的差模增益为Ad、输入电阻为rid、输出电阻为ro，则RC非对称文氏桥振荡电路等效电路图如图1所示。由文献[6]可知，当rid→∞和Ad→∞，则该振荡电路的起振平衡条件为：

(1)

振荡频率为：

(2)

由式(2)可以看出，当运放的rid→∞、Ad→∞时，运放的输出电阻ro对起振条件和振荡频率没有影响，并且若用R1调节振荡频率ω0，当R1减小时，为使得ω0与R1有单调递增关系，式(2)中R1的取值必须满足：

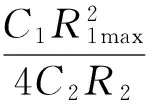
(3)

式中，R1max为可变电位器R1的最大值。

2 稳幅环节的设计与相关分析

稳幅环节的设计思路是在参数C1、C2、R2、R3、R4恒定的条件下，减小因频率调节(调节R1)对反馈系数的影响，这样使得自动增益控制稳幅环节易于实现，即令：

C2/C1≫1R1/R2<1

(4)

设通过R1调节频率时的变化量为dR1，若采用R3调节增益，其变化量为dR3，则对式(1)微分可得：

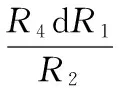
(5)

根据式(3)取：

(6)

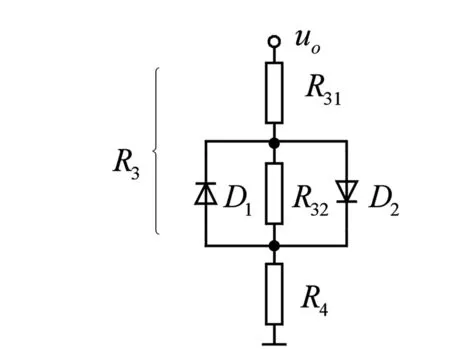
图2 稳幅环节电路

由式(4)、(5)可知有R3≫R4。利用二极管构成的稳幅环节如图2所示，其中R3由R31、R32和二极管D1、D2构成，并且设D1、D2正向导通的等效电阻为rD1、rD2(rD1=rD2=rD)，则R3可表示为：

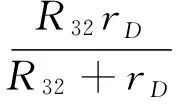
(7)

式中，rD=UD/ID，UD、ID分别为正弦波信号加载在D1、D2上有效值电压和电流。

当调节频率变小、增益不变的条件下，输出幅度减小，由此将引起D1、D2上有效值电压和电流减小，由此引起rD增加，则有：

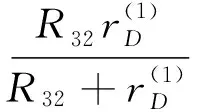
(8)

(9)

且有：

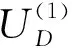
(10)

(11)

在频率最大时，使输出正弦波不失真幅度达到最大，以此确定稳幅环节中元器件参数R31、R32、R4并且保持不变，增大R1使频率减小，输出正弦波不失真幅度也将减小，若过小则将导致停止振荡。

3 仿真结果与分析

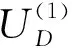
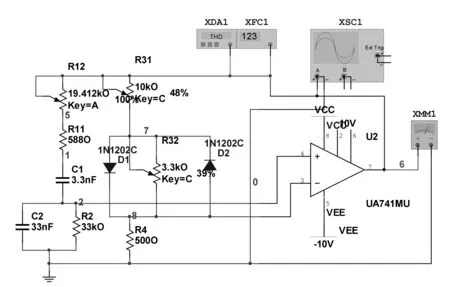
图3 非对称文氏桥振荡器仿真电路图

电路振荡调试包括如下步骤：①频率高端调节。首先将R1调节至最小(即R12=0)，此时频率最大，将R32和R31置于最大，逐渐减小R31使输出端产生不失真的正弦波，随后使R31固定不变。②频率低端调节。将R1调节至最大，此时输出幅度将减小，逐渐减小R32至设定的输出幅度最小值Uom min。

在振荡器调试过程中，R31由最大调整至设计值附近时，才能产生不失真幅度Uom(有效值)较大的正弦波，继续减小R1，Uom也将急剧减小，并且总谐波失真(Total Harmonic Distortion，THD)也将增大。因此，仿真试验表明，当R31调整为10kΩ电位器的48%时，Uom达到最大，与设计值4.79kΩ趋于一致。

表1所示为R31位于10kΩ电位器的48%时，将R32(3.3kΩ)电位器从100%逐渐减小使得Uom很小或停止振荡时的仿真结果。从表1可知：①无论是在哪个频率(f0)点，随着R32的减小，f0将增加(很小)，但Uom也将减小(较为显著)，若考察Uom下降为最大Uom的90%的频率，则f0相对误差最大不超过0.63%；当R32大于设计值1.01kΩ时，Uom下降不超过3dB。②无论是在哪个频率点，随着R32的减小，THD将减小。③当R32一定时，增加R12，则f0下降，Uom显著减小(最大达-12dB)，说明二极管稳幅效果非常有限。

表1 R32可变时输出正弦波的仿真结果

4 结 语

在非对称文氏桥振荡电路中，要在整个频率范围内实现R3的平衡较为困难。利用二极管的非线性特性来实现放大环节的自动稳幅，并给出了稳幅环节参数的计算方法。仿真结果表明该计算方法是可行的，同时也表明采用二极管稳幅效果非常有限，对此可以考虑增加热敏电阻来参与稳幅。

[1]Abdellah A G. Experimental observation of chaotic properties in a system of two coupled Wien-Bridge oscillators [J]. Chaos,Solitonsand Fractals, 2007(32)：988-995.

[2]华成英.模拟电子技术基本教程[M].北京：清华大学出版社,2006.

[3]田社平，蔡萍， 陈洪亮，等.文氏桥式振荡电路特性及数值仿真分析[J].电气电子教学学报, 2007,29(3)：38-40.

[4]李永安.文氏桥振荡器实验中两个现象的分析[J].大学物理实验, 2005,18(2)：34-37.

[5]陈宇宁，卢成健.RC桥式振荡器起振条件的研究及其仿真[J].玉林师范学院学报(自然科学), 2004,25(5)：38-41.

[6]邹学玉. RC文氏桥振荡器振荡条件的研究[J].长江大学学报(自然科学版)，2011，8(6)：104-105.

[编辑] 李启栋

10.3969/j.issn.1673-1409.2011.08.029

TN752

A

1673-1409(2011)08-0091-03