基于遗传算法的变频调速泵站优化运行

2011-11-18汪建华

长江大学学报(自科版) 2011年22期

关键词：扬程并联泵站

汪建华

(长江大学机械工程学院，湖北荆州 434023)

基于遗传算法的变频调速泵站优化运行

汪建华

(长江大学机械工程学院，湖北荆州 434023)

调速泵站在流量及水源水位变化时，若水泵运行组合不合理，导致泵站运行效率低。在考虑泵并联运行时进水管和连接管水力损失的基础上，提出以泵开机状态和调速率为设计变量，泵站流量和调速泵调速范围为约束条件，泵站总功率最小为目标函数的优化运行数学模型，并采用遗传算法对模型进行了求解。优化结果表明，模型及求解方法有效，可适用于调速泵站的优化运行。

变频调速；水泵并联；优化运行；数学模型；遗传算法

近年来，随着科技的进步, 变频调速装置得到广泛应用。泵站采用变频器能调节控制水泵机组电动机的转速，具有调速范围宽、流量调节连续、显著降低节流损耗及启动水泵机组电动机时电流平稳等优点，因而许多泵站装配了调速装置。为此，研究调速泵站的优化运行具有重要意义。调速泵站的优化运行是在泵管路装置和流量一定的条件下，通过改变泵转速、增减泵的运行台数，使泵站总能耗最小，从而达到优化运行的目的。许多研究者[1-3]建立离心泵并联优化运行的数学模型时，忽略了各泵的进水管和连接管中的水力损失，将同一扬程下各泵的流量相加得到多泵并联运行的总流量，从而导致计算结果不准确。调速泵站优化运行属于连续/离散混合非线性规划问题，采用传统的优化方法求解时效率低、精度差。基于此，笔者采用求解连续/离散混合变量问题能力较强的遗传算法[4]对调速泵站的优化运行模型进行求解。

1 泵站优化运行的数学模型

1.1离心泵的特性曲线

设泵站共配置n台调速离心泵，第i台泵在额定转速下的特性曲线由产品样本确定。通过对泵特性曲线进行拟合，则第i台泵在额定转速下的流量(Qi)～扬程(Hi)表达式Hi=f(Qi)和流量(Qi)～功率(Pi)表达式Pi=f(Qi)为[2]：

(1)

(2)

式中，Qi为泵流量，m3/s；Hi为泵扬程，m；HXi为泵流量为零时的虚扬程，m；SXi为泵虚阻耗系数，s2/m5；Pi为泵流量轴功率，kW；ai、bi、ci和di为泵轴功率的拟合系数,其单位分别为kW、kW·s/m3、kW·s2/m6和kW·s3/m9。

根据比例定律，第i台泵在调速率ki下的扬程和功率分别为：

(3)

(4)

式中，ki为第i台泵的调速率，ki=ni/n0i，n0i、ni分别为第i台泵的额定转速和工作转速，r/min。

1.2管路装置扬程

水泵并联系统示意图如图1所示。n台并联泵通过公共节点A联合向主管路AB供水，第i台泵将水从吸水池输送到排水池所需要的能量为：

(5)

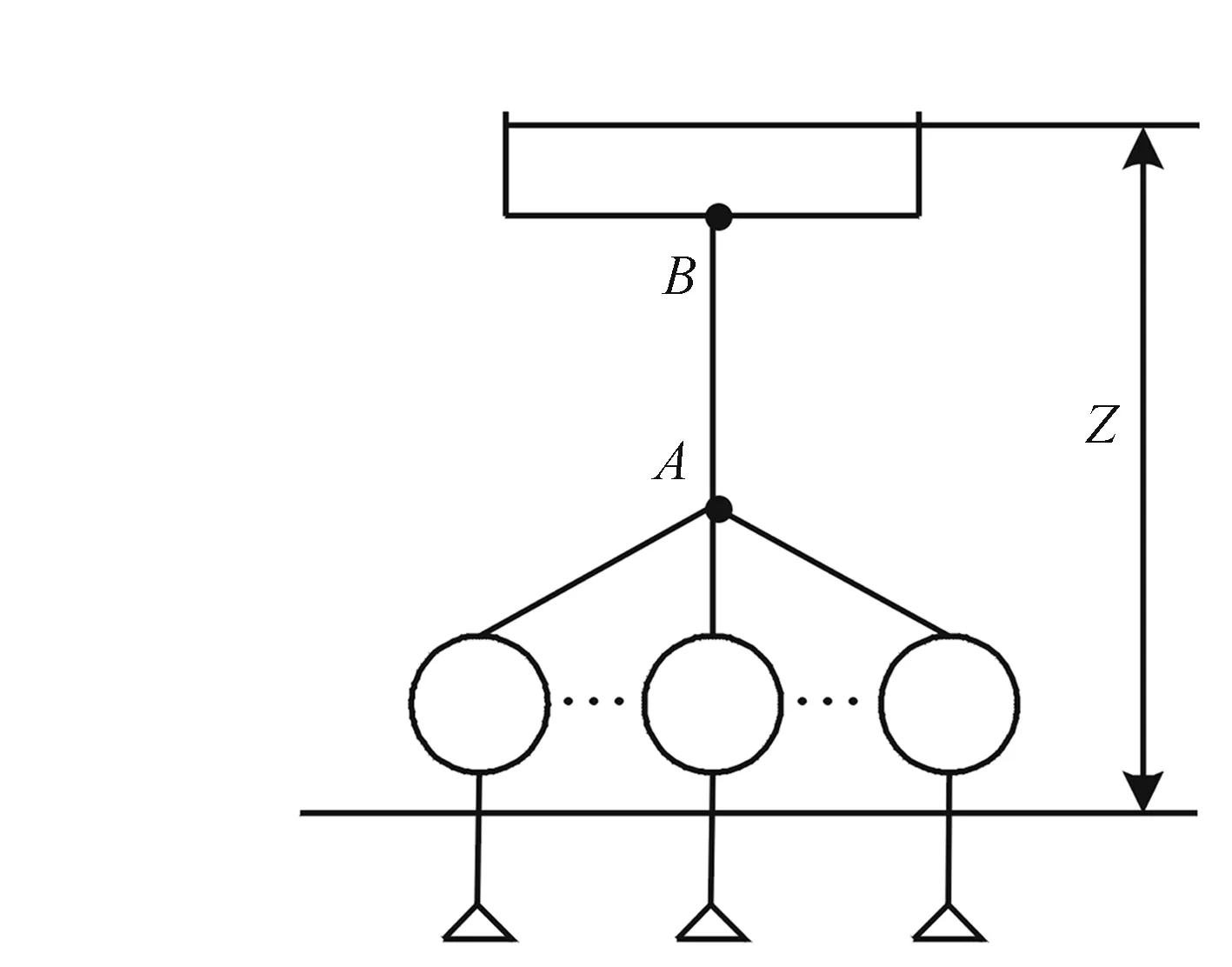
图1 水泵并联系统示意图

式中，Hi为第i台泵扬程或装置扬程，m；Z为排水池液面与吸水池液面之间的高度差，m；Si为吸水池至公共节点A间的管路阻力系数，s2/m5；S为主管路AB的阻力系数，s2/m5；Q为泵站总的供水量，m3/s。

1.3单泵流量

根据式(3)和式(5)，泵在图1所示装置中的扬程为：

则单泵流量为：

(6)

由式(5)和式(6)可知，在确定并联各泵实际运行流量时，当管路系统各分支管路长度、直径、流量等不相等而导致各分支管路的阻力损失相差较大时，则各泵的扬程相差也较大。

1.4数学模型

1 )目标函数泵站优化运行的目的是在将水按要求的流量从吸水池输送到排水池的前提下达到能耗最少，即泵站水泵机组总的轴功率最小。因此，泵站优化运行问题可描述为对于给定的泵站并联管路装置系统，在已知调速泵台数n、泵站总流量Q的条件下，确定并联运行泵的台数m(m≤n)和调速率ki(i=1,2,…,m),使泵站水泵机组总的消耗功率最小。目标函数为：

(7)

式中，μ为状态因子，μi=1表示第i台泵投入运行，μi=0表示第i台泵未投入运行。

2) 设计变量将单泵流量表达式(6)代入目标函数表达式(7)可知，优化运行的的设计变量为各泵的状态因子μi和调速率ki。

X=[μ1,…,μn,k1,…,kn]

(8)

3)约束条件为使水泵机组高效、安全运行和满足流量要求,仅需考虑调速率约束和总流量约束2个约束条件。

(9)

总流量约束为：

(10)

因此，并联调速泵站优化运行问题是在满足约束条件式(9)～(10)的条件下，求出μi和ki，使目标函数达到最小，从而实现泵站的高效运行。

2 模型求解

采用遗传算法求解数学模型时，需对设计变量μi、ki进行编码。状态因子μi是离散变量，可直接采用二进制编码。调速率ki是连续变量，对其进行离散化处理后再采用二进制编码。每台调速泵采用8位编码，最高位为1表示调速泵开启(μi=1)，最高位为0表示调速泵停机(μi=0)。低7位表示调速泵的调速率ki，共有128种转速状态，0表示调速泵最低调速率，127表示调速泵最高调速率。假定泵站共有n台调速泵，则n台泵机组共有8n位编码。编码确定后，对约束条件采用模拟退火罚函数法，将带约束优化问题化为无约束问题[5]。

3 仿真算例

某泵站并联设置4台调速泵，其中1#、2#泵为200S42型，3#、4#泵为250S39型，吸水池至公共节点间的管路阻力系数Si=175.4s2/m5(i=1,…,4) ，公共节点至排水池间的管路阻力系数S=221.1s2/m5，排水池液面与吸水池液面之间的高度差Z=6.5m。当泵站总流量要求为0.35m3/s时，求泵站最优运行参数。

由泵产品样本资料[6]拟合得到200S42型泵在调速率为k时的扬程和轴功率表达式分别为：

H=57.30k2-2504.9Q2P=9.512k3+7.714×102k2Q-7.560×103kQ2+2.948×104Q3

250S39型泵在调速率为k时的扬程和轴功率表达式分别为：

H=46.87k2-535.3Q2P=28.31k3+259.3k2Q+299.4kQ2-2685Q3

4台泵机组共32位编码。取种群规模为160，选择概率0.02，交叉概率0.55，变异概率为0.007，温度冷却参数为0.998，结束条件为迭代200代。编程计算所得到的泵站总耗电功率为150.52kW，而优化前泵站总耗电功率为153.80kW，优化后泵站节电约3.28kW。优化前、后每台泵详细运行情况如表1所示。