一种改进的并行干扰抵消检测算法

杨 梅，陈 阳

(安徽工程大学现代教育技术中心，安徽 芜湖 241000)

一种改进的并行干扰抵消检测算法

杨 梅，陈 阳

(安徽工程大学现代教育技术中心，安徽 芜湖 241000)

为了抑制V-BLAST系统的多流干扰，最优算法是最大似然检测算法，但由于该算法计算复杂度太高而无法实际应用。针对该问题，给出一种新的检测方案，即首先采用最小均方误差算法进行初始估计，再采用改进的并行干扰抵消算法来抑制多流干扰。仿真结果表明，该算法有较强的抗多流干扰能力，性能接近最大似然检测算法，但其复杂度较低且时延较小。

多流干扰；MMSE估计；并行干扰抵消算法

研究表明，在瑞利衰落信道下，多输入多输出系统通过多发射天线或者接收天线可以显著提高无线通信系统的信道容量[1]。为了实现这个容量，Foschini等[2]提出贝尔实验室贝尔分层空时结构 (BLAST)。该结构可以近似实现容量的下界，能够依靠接收端的信号处理技术来实现具有合理复杂度且近似接近中断容量的性能，从而实现高速数据传输[3]。1998年，Wolniansky德[4]提出垂直贝尔实验室分层空时码(V-BLAST)。V-BLAST是一种典型的空分复用系统，能够极大地提高系统频谱利用率。V-BLAST结构简单，各个数据流间不需要相互正交，而是利用多径时延保持相互独立。然而，实际通信过程中，各数据流间并不完全独立，相互之间存在一定影响，从而导致多流干扰(Multi-Stream Interference，MSI)现象[5-6]。解决多流干扰的方法是构建接收端的信号检测算法，其中最优算法是最大似然(Maximum Likelihood，ML)算法，但ML算法指数复杂度太高，不利于实时实现。为此，相关学者提出了排序串行干扰抵消(Order Successive Interference Cancellation，OSIC)[7]和广义并行干扰抵消 (Generalized Parallel Interference Cancellation，GPIC)[8]等一系列次佳检测算法。然而，OSIC算法需要对信道矩阵求伪逆，得出一个迫零向量，而且每次求伪逆后还要进行排序操作。在发射天线数比较多的情况下，算法复杂度很高且时延较大，同时有误码传播现象[7]。所以在实时通信系统中也很难实现。GPIC算法需要对信道矩阵分割，然后采用2次并行干扰抵消(前抵消和后抵消)，最后进行最小欧式距离判决[6,8]。但是随着分割矩阵列的增多，复杂度增加且结构较复杂。为此，笔者给出一种新的检测算法，该算法首先采用最小均方误差(Minimum Mean Square Error，MMSE)算法进行初始天线的估计，然后利用改进的并行干扰抵消(Improved Parallel Interference Cancellation，IPIC)算法解决多流干扰问题。

1 V-BLAST系统模型

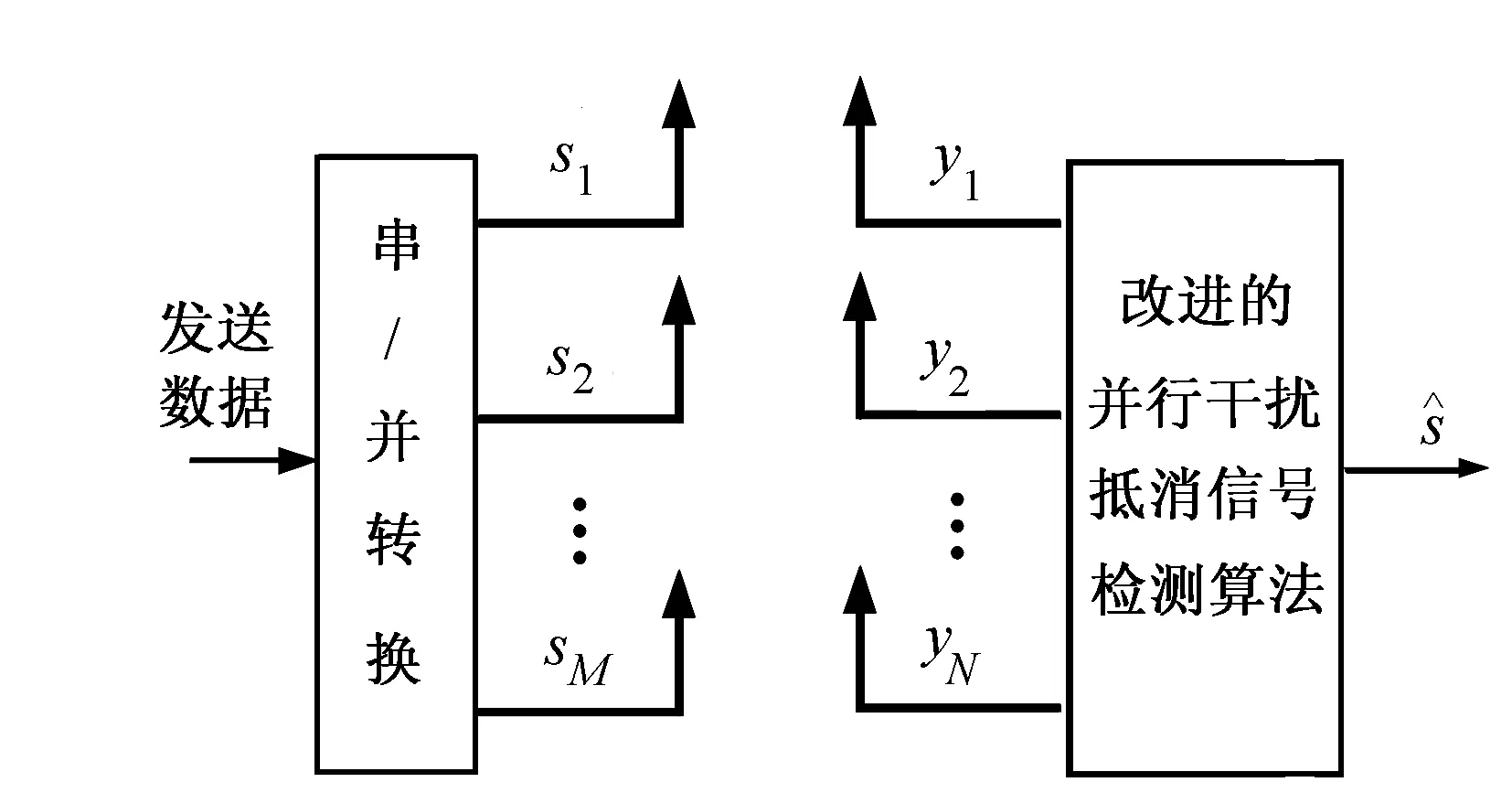
图1 V-BLAST系统示意图

(1)

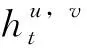
为了叙述方便，将式(1)所示的接收信号表示成矢量形式[5]：

y=Hs+n

(2)

式中，y=(y1,y2,…,yN)T是N×1维接收信号矢量；s=(s1,s2,…,sM)T是M×1维发射信号矢量；H为N×M的信道传输矩阵；n=(n1,n2,…,nN)T是N×1维加性高斯白噪声矢量；方差矩阵为2σ2IN(IN是N×N单位阵)。

V-BLAST检测的目的是在已知H(假设接收端完全已知信道的信息)和y的前提下,根据不同检测算法来获得最佳有用信号。在不同检测算法中，最大似然检测算法性能最优，其在整个向量空间内进行遍历搜索，通过求解似然函数的最小值形成最佳信号矢量，其标准化形式为[5]：

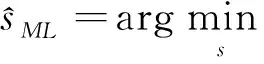
(3)

最大似然检测算的复杂度随着发送天线的增加呈指数增加，尽管其误码率很小，但由于该算法计算复杂度太高而无法实际应用。一般OSIC要根据信噪比(SNR)的高低来决定最优的检测顺序，根据不同准则产生迫零矢量，对应的算法为迫零-排序串行干扰抵消算法(Zero Forcing-Order Successive Interference Cancellation，ZF-OSIC)和最小均方误差-排序串行干扰抵消算法(Minimum Mean Square Error- Order Successive Interference Cancellation，MMSE-OSIC)。ZF-OSIC算法是基于迫零矩阵将接收信号分解成M个独立的数据流，可以完全抑制多流干扰，但是在分解信号过程中会增加噪声功率；MMSE-OSIC算法则克服了ZF-OSIC在运行过程中噪声功率会增加的缺点，其性能略优于前者，但是它无法形成独立的数据流。此外，OSIC算法需要M次伪逆操作，M次排序运算，其计算量很高，时延很大，难以实时实现。为此，笔者提出了一种新的检测算法，即改进的并行干扰抵消信号检测算法。

2 改进的并行干扰抵消信号检测算法

改进的并行干扰抵消信号检测算法由基于最小均方误差的初始估计算法和一个IPIC检测算法器组成，通过以下2个主要步骤实现抑制多流干扰，恢复发送信号。

2.1基于MMSE的初始估计算法

该检测方案在收到信号后，首先根据MMSE准则构造权向量矩阵[5]：

G=(HHH+σ2I)-1HH

(4)

式中，上标‘H’表示矩阵的共轭转置；‘-1’表示非奇异阵的逆。

其次，对G矩阵中的行向量按其范数大小进行排序：

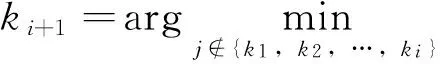
(5)

式中，‖·‖表示范数运算。

再按照上述顺序逐次抵消各个数据流的干扰，形成发送信号s的软判决统计，即：

r=Gy

(6)

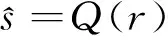
(7)

式中，Q(·)表示硬判决操作。

2.2改进的并行干扰抵消检测算法

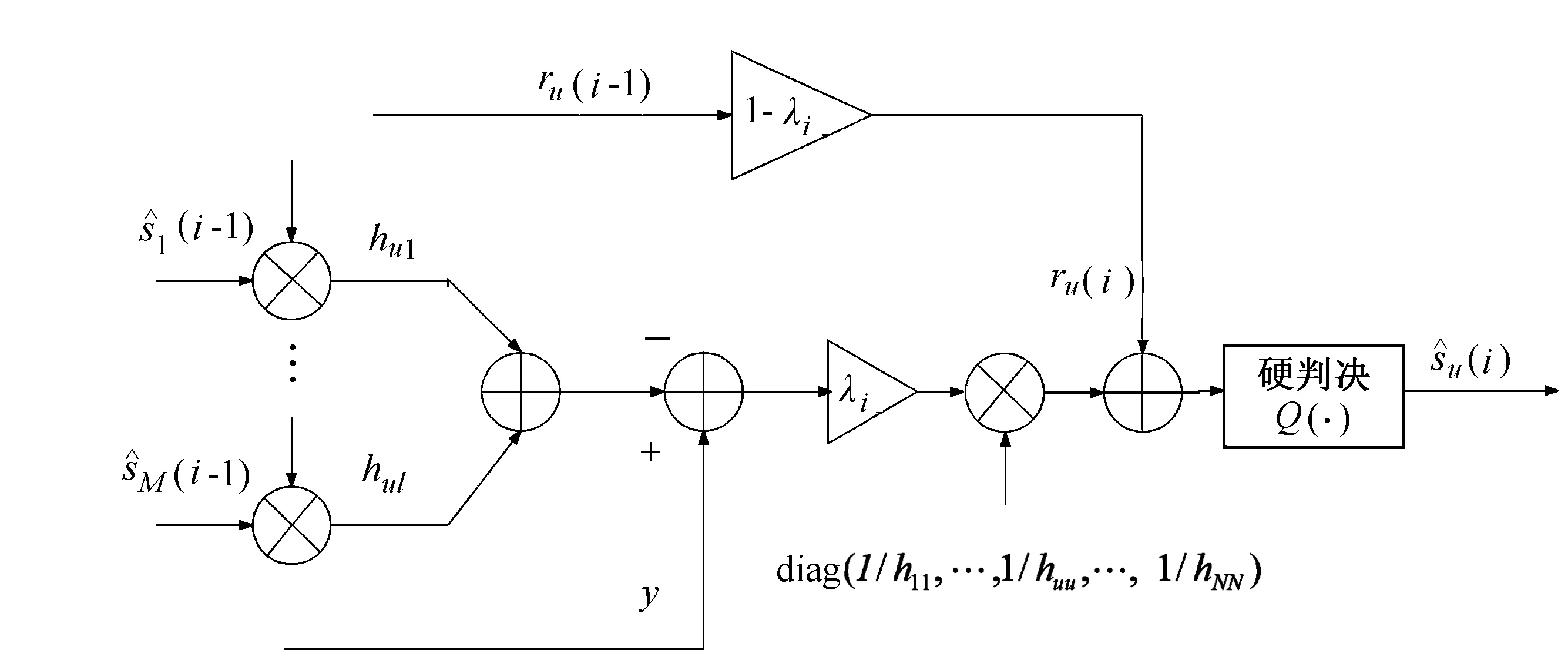
图2 第u根天线在第i级抵消干扰示意图

IPIC检测算法是对所有天线的干扰并行估计和抵消，通过其他发送天线信号以前的判决量逐步抵消待检测天线的信号中出现的多流干扰成分，即算法的第i步要用第i-1步的判决量来抵消接收信号中的多流干扰[6,9]。IPIC与并行干扰抵消(Parallel Interference Cancellation，PIC)相比，不是在每一步都根据估计值抵消“所有的干扰”，而是在每一步根据估计值的可信度，引入一个部分抵消因子λi来抵消多流干扰中的一部分。该因子可以减小前一级的误码传播，从而避免性能的衰减[6,10]。研究表明，λi随着级数的增加而单调增加，但是始终限制在0～1范围之内[10]。

各根天线同时进行IPIC，从而实现基于多级的IPIC算法[10]。图2给出了任意一根天线在第i级的部分抵消干扰的过程[7]，其中hu1,hul(l=1,2,…,M,u=1,2,…,M,l≠u)表示干扰矩阵H_interf的元素。首先得出发射信号s第i步的软判决统计：

(8)

3 仿真结果和性能分析

假设一个平坦衰落信道中的V-BLAST系统，且信道衰落相对于信号传输速率来说变化缓慢，且信道衰落在一个数据帧内的变化可以忽略不计。

图3所示为V-BLAS系统采用不同检测算法时的误码率和信噪比变化曲线图。仿真环境针对5×5(M=N=5)的V-BLAST系统，且每个发射机均采用QPSK调制。从图3可以看出，ML性能最好，MMSE-OSIC优于ZF-OSIC算法，改进的并行干扰抵消信号检测算法略优于MMSE-OSIC。在误码率10-3数量级时，改进的并行干扰抵消信号检测算法非常接近MMSE-OSIC算法的性能。

图4所示为改进的并行干扰抵消信号检测算法在采用不同发射天线和接收天线时的误码率和信噪比变化曲线图。从图4可以看出，误码率随天线数的增加而增大。

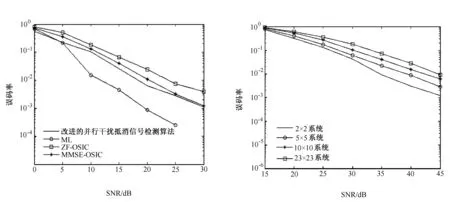
图3 ZF-OSIC、MMSE-OSIC、ML以及改进的并行干扰抵消信号检测算法的性能比较 图4 改进的并行干扰抵消信号检测算法在不同天线下的性能比较

4 结 语

MMSE-OSIC算法需要M次伪逆运算和M次排序运算，其时延较大。利用改进的并行干扰抵消信号检测算法，只需要1次伪逆运算和0次排序运算，其时延较小，该算法在一定程度上降低了计算复杂度，节省了大量时间，所以更有利于在通信系统中实现。

[1]黄韬. MIMO相关技术与应用 [M].北京：机械工业出版社, 2007.

[2] Foschini G J. Layered Space-time Architecture for Wireless Communication in Fading Environments when Using Multiple Antennas [J].Bell Labs Technical Journal, 1996, 2: 41-59.

[3] Gamal H E, Hammons A R. A New Approach to Layered Space-Time Coding and Signal Processing [J]. IEEE Transactions on Information Theory, 2001, 47: 509-519.

[4] Wolniansky P W, Foschini G J, Golden G D，et al. V-BLAST: An Architecture for Realizing Very High Date Rates over the Rich-scattering Wireless Channel [A].Pisa, Italy. Proceedings of the URSI International Symposium on Signals, Systems, and Electronics, ISSSE 98 [C]. Piscataway, USA: IEEE Inc，1998: 295-300.

[5] Mhjinder J. Space-Time Codes and MIMO Systems [M]. London: Artech House，2004:137-164.

[6] 倪梁方, 杨梅, 王培珍. V-BLAST系统中改进的并行干扰抵消信号检测算法 [J]. 安徽工业大学学报(自然科学版)，2010,27(2):180-184.

[7] Golden G D, Foschini G J, Valenzuela R A，et al. Detection Algorithm and Initial Laboratory Results Using V-BLAST Space-time Communication Architecture [J]. Electron Letter, 1999, 35 (1):4-16.

[8] Luo Z D, Zhao M, Liu S Y, Liu Y N. Generalized Parallel Interference Cancellation with Near-optimal Detection Performance [J]. IEEE Transactions Signal Processing, 2008, 56(1): 304-312.

[9] Divsalar D, Simon M K, Raphaeli D. Improved Parallel Interference Cancellation for CDMA [J]. IEEE Transactions Communication, 1998, 46:258-268.

[10] Varansai M K, Azhang B. Multistage Detection in Asynchronous Code-division Multiple-access Communication [J]. IEEE Transactions Communication, 1990, 38(4):509-519.

[编辑] 李启栋

10.3969/j.issn.1673-1409.2011.08.025

TN929.5

A

1673-1409(2011)08-0078-03