如何培养学生数学的创新能力
2011-11-13李明生
李明生
如何培养学生的创新素质是当前教学研究的重要课题,不仅是对数学提出的更高层次的要求,也是当前数学素质教育的需要。创新精神的培养是创新教育的最高境界,它可以分为怀疑精神、开拓精神和求实精神。
1怀疑精神
我们的学生往往缺乏怀疑精神,所以经常“惟书、惟师”而难以取得创新成果。欲立先破,应激励学生大胆怀疑,摆脱传统羁绊,同时创设民主宽松的和谐氛围,为优秀人才的脱颖而出创造条件。
2开拓精神
以创新为荣,以创新为乐。发挥创新潜力,坚定创新意志。
3求实精神
科学研究必须实事求是,来不得半点虚假和空想。因而数学教育实践中更需要培养学生求实精神。
为了让学生由被动消极学习转变为积极探索,主动学习在解决问题的过程中不断发现新问题,这对培养学生科学的研究和探索精神是十分必要的。
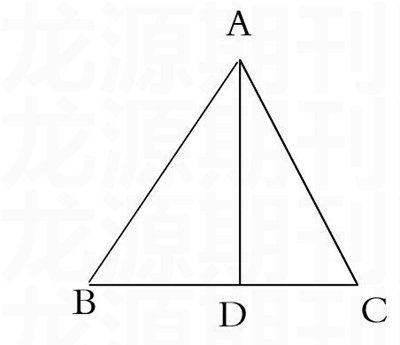
如右图:等腰三角形的两个底角相等。①引导学生自己写已知、求证、画图。②分析如何证两个角相等,转化成归结到两个三角形中证全等。③想想如何添辅助线,鼓励学生分别去探索。④找学生做。
已知:在△ABC中,AB=AC
求证:∠B=∠C
证法:作BC边的高AD
∴∠ADB=∠ABC=90°
在Rt△ABD和RtACD中
AB=ACAD=AD
∴Pt△ABD≌Rt△ACD(HL)∴(1)∠B=∠C
教师提问:由全等还可以证出什么?
学生:①∠BAD=∠CADAD是项角的平分线。②BD=DC D是BC的中点。
教师总结:等腰三角形的高线也是项角的平分线,底边上的中线,再找学生证另两种证明。用类同的方法得出:
推论:等腰三角形的高线、中线与顶角的平分线三线重合。
【评论】①通过一题多解可以沟通各种知识的内在联系,使已学知识形成系统。同时,学生也学会了从不同的角度去观察思考问题,遇到问题时,能多向联想、随机应变,提高学生的应用能力。②体验化归思想。③教师充分启发学生自己思考,使他们自己去积极地发现和提出问题,并通过尝试与假设,努力去解决问题,从而激发了学生的创新精神。这种观
点是包括布鲁纳在内的许多心理学家极力倡导的。
等边三角形是特殊的等腰三角形,除具有等腰三角形的性质外,还有特殊的性质吗?
根据下列条件求等腰三角形中其余两个角的度数。①顶角是70°;②一个底角是45°;③一个底角为60°;④一个角是30°;⑤一个外角是70°。
通过具体的循序渐进的题目,应用所学数学知识,指导学生进行巩固性练习和变式练习。要想做对,就要有敏锐、全面的观察力,变通、灵活的思维能力,同时也要渗透分类思想。由此可见。“等边对等角”这个定理,提示了同一个三角形边和角之间的关系,于是联想:“同一个三角形中,等角对等边吗?大角对大边吗?”等腰三角形“底边上的三条主要线段互相重合”,可见这条特殊线段有三种不同的“身份”。因此,它是推证两条线段相等,角相等以及两条直线互相垂直必须关注的“热线”。
创新能力的培养是当今教育界的发展趋势,中学生是思想最活跃、最富想象力的群体,加之数学学科以其知识的抽象性、规范性特点,为教师在教学过程中培养创新能力提供了广阔的空间。培养学生的创新能力需要让学生在教师精心创设的情境中用自己的思维方式学习知识,发现未知世界,这样,学习的主动性、创造性才能得以体现和发展。没有接受创新教育的学生,往往认为创新太难,是创造发明家的事,为了扣开创新的神奇“面目”,培养学生创新信心,使学生感到创造是每一个人都能做的事,一方面向学生介绍一些古今中外创新的例子,另一方面,通过引导学生创造性地解决问题,让学生获得成功,增加创造信心。学生是教学活动的主体,实施创新教育让学生主动参与,发挥主体的积极作用,必须要有合理的教学组织形式,让学生有充分的思维活动时间和空间,为此,教师要为学生提供观察、调查、动手操作、思考表现的机会,分类指导,分层教学,提高学生参与效果,充分挖掘每个学生的创新潜能,发展学生的创新个性。
总之,教师要以先进的数学教学理论、数学教学思想为指导,充分利用现代化的教学技术,善于改革与创新,特别要注意克服运用过程中的单一化,要根据不同的教学内容、教学对象,课型以及教师自身特点,灵活处理各个环节的设计,贵在有意、有机,贵在用活。在数学教学中,培养学生的创新能力的方法有很多,需要我们在实践中不断发现和总结。今天的教育是未来世界的蓝图,是我们教育工作者义不容辞的责任。
