模糊随机供需变量的VM I的订货量模型

李丽

(1.同济大学经济与管理学院，上海201804；2.德州学院计算机系，山东德州253023)

模糊随机供需变量的VM I的订货量模型

李丽1，2

(1.同济大学经济与管理学院，上海201804；2.德州学院计算机系，山东德州253023)

VM I（Vendor Managed Inventory，供应商管理库存）环境是一个不确定的环境。由于不能准确地刻画需求与供给的变化，使得供应商不能很好解决按需订货问题，库存成本居高不下。文章将ADI（Advance Demand Information，预求信息）和准时到货率描述为模糊随机变量，更客观地反映了市场情形。为了在模糊随机环境下得到供应商的订货量，基于模糊随机理论，对传统EOQ模型进行了扩展，提出了模糊随机供需变量的VM I的订货量模型。对特殊的模糊随机供需变量的情形，不仅能够得出最优订货量，有效降低库存费用，而且能够分析供应商的费用随库存管理费用变化的情况，使得在不确定环境下决策时能利用更多的信息。

供应商管理库存；模糊随机变量；预求信息；准时到货率；最优订货量

0 引言

VMI（Vendor Managed Inventory，供应商管理库存）是一种在购买商占优的市场环境中出现的一种供应链库存管理模式[1]（Tyan和Wee，2003）。在生产提前期（对客户来说，称需求提前期）长的供应链中，常采用VMI的管理模式，如图1。需求提前期较长的客户在需要之前下订单时的需求信息，为预求信息（Advance Demand Information，ADI）。购买商为了帮助供应商更好地感知需求，借助于电子商务，为供应商提供ADI（如购买商公布的生产计划信息）。例如Ford公司和GM公司向其供应商发布ADI并且每周更新订单[2]。

VMI中，由于供应商管理库存，用户和供应商之间合作，双方可以更好地兼顾供应和需求以减少大量冗余库存。对于需求和准时到货率，由于企业积累了用于拟合其概率分布的历史数据，虽然数据有限并且不完全可靠，但用随机变量来描述有一定的合理性。另外，需求和准时到货率还是库存管理中不能清晰界定的信息，可以按照专家的经验估计其值，用模糊变量来描述也有其合理性。可以说需求及准时到货率的模糊性、随机性是交织在一起出现的。而在一些文献中，需求和供应被看作随机变量或模糊变量，这样刻画很难准确描述企业真实情况。当有最多两年的历史数据时，ADI和准时到货率等都可以被刻划为模糊随机变量。基于模糊随机变量建模得到的结果与实际情况接近，因而更加实用。因此，本文研究模糊随机供需变量的VMI的订货量模型。

1 模糊随机供需变量及其数学描述

1.1 模糊随机需求的数学描述

Liu Y和Liu B[2]（2003年）给出了独立同分布的模糊随机变量的概念，同时也给出了模糊随机变量的纯量期望值算子的定义。

定义1[2]（Liu Y和Liu B，2003）假设ξ是一个从概率空间(Ω,A,Pr)到模糊变量集合的函数。如果对于R上的任何Borel集B，Cr{ξ(ω)∈B}是ω的可测函数，则称ξ为一个模糊随机变量。

VMI中，下游企业的ADI是供应商确定订货量的一个因素。由于从供应商确定订货量到下游企业实际使用这批订货，经历的时间较长，原预测的市场情形可能变为下游企业减产（与订货时预测的数量相比）、增产等。各情形下的需求量管理者根据经验可估计，各种市场情形服从的概率分布由历史数据可统计。用模糊随机变量刻画需求是合适的。根据定义1，设需求是一个从概率空间(Ω,A,Pr)到模糊变量构成的集合的函数。为正的模糊变量（例如三角模糊变量、梯形模糊变量等）。假设与订货时间点下游企业发布的生产计划相比，不确定市场环境下存在种随机市场情形，如下游企业减产、产量与订货点公布的计划相近、增产等，用ωi表示第i种市场情形（如用表示下游企业减产），每种情形发生的概率分别为p1，p2，…，pn。i=1,2,…，n可将需求表示为如下形式：

根据Liu和Liu[3]的定义，由于式（1）中的为正的模糊变量，则的期望值为的隶属函数为ui，根据Liu[4]的定理，则：

因此，本文给出在一定订货批量下，模糊随机需求的期望值的计算公式：

（1）式定义的需求可看作是最简单形式的模糊随机需求。模糊随机需求还可以表示为关于随机变量的其它形式的模糊变量。

1.2 模糊随机准时到货率的数学描述

生产提前期长的行业的生产环节存在对订单产品的顺利生产有很大的影响的不确定因素。假设不确定生产环境下存在n种随机情形，如机组产能稳定、瓶颈工序积压、机器发生故障等，用表示第i种随机生产情形，每种生产情形发生的概率分别为根据定义1，本文将准时到货率表示为如下形式：

（4）式定义的模糊随机准时到货率可看作是最简单形式的模糊随机变量。模糊随机准时到货率也可以被刻画为其他模糊随机变量形式。

3 问题描述、假设及符号

当前，VMI中，下游的购买商对上游供应商的产品满足市场需求的速度提出了很高的要求，越来越多的企业要求供应商采用JIT(Just In Time，准时化)供应。供应商为了及时响应需求，防止不能按时交货，通常要储备大量的库存，以应付需求量的增加以及上游生产商交货的不稳定，造成了高额的运行成本，严重影响了企业的竞争力。

造成企业库存量大、库存成本高的原因有很多，除了需求和供给的不确定因素外，还有一个原因是VMI企业没有一个合适的订货量模型。企业在不确定的环境下运营，订货量模型不合适的结果是要么有可能发生缺货，不能及时满足需求，要么造成库存量大，库存成本居高不下。在供需变量为模糊随机变量的VMI中，供应商面临的问题是，如何在满足对下游企业供应的基础上，决策最优的不允许缺货的订货量，使存储系统总费用最小？

由于JIT供应下，供应商缺货将导致包括产品相应的利润、下游企业因缺货而停产、失去供应链的长期合作伙伴等损失，这些损失远远超过了产品的存储成本。因此，在这里视为不允许缺货的模型。具有一定生产周期的行业一般采用定期订货模式，因此，本文假设定期订货、一次性到货。

假设一对一的供应链，即购买商只从一家供应商处采购，而供应商也只为这一家购买商供货，购买商的销售量就是供应商的采购量，且供应商是这种关系的主导者。单一产品。此外，假设具有预算资金和存储空间的约束。

为了表述问题的方便，列出其它一些符号。

T以周为单位的周期（采购量消耗期）；

L订货提前期；

B1供应商每周期最大的资金约束；

B2供应商的最大存储量；

c1供应商单位产品的订货、生产准备、生产及配送成本之和；

h供应商的单位产品的存储成本。

4 模型的建立

VMI模式下（如图1），供应商根据组织内生产部门的供应信息和组织外企业的需求信息做订货决策。根据传统库存控制理论和EOQ模型的思想，决策VMI的订货量时，与订货量有关的因素为持有库存量、最小存储系统总费用、可用资金、最大库存容量、需求量等。经典EOQ是针对单个企业而言的，订货模式如图2。经典EOQ模型假设需求为确定值，而很多情况下需求量为模糊随机变量；经典EOQ模型假设当存储降为零时，可以立即得到补充并且所要补充的数量全部同时到位，而很多行业生产周期长，无法随时补货。经典EOQ模型没有供应变量，而VMI中准时到货率也作为决策订货量的一个模糊随机变量。因此需对EOQ模型进行扩展。

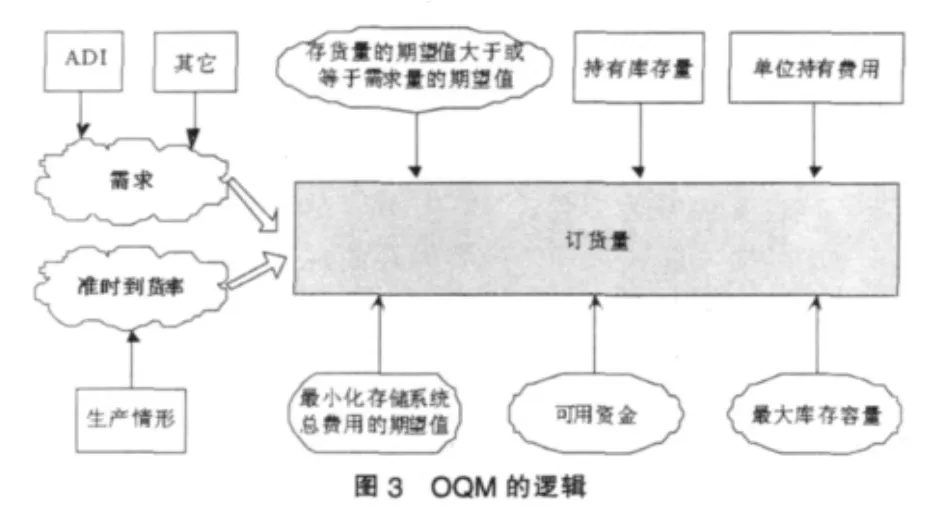
常见订货量模型问题的研究多为确定型的和随机型的，本文研究模糊随机型订货量模型。本文模型与传统EOQ模型不同的是需求量为模糊随机变量，同时又添加了准时到货率变量，而且准时到货率也是模糊随机变量。解决模糊随机库存问题的主要方法是对经典库存模型进行扩展。Das等[5]（2004）研究了模糊随机环境下的库存问题。然而这些研究只给出了适用于一些特殊的模糊随机环境下的库存优化方法，没有给出需求与供应的模糊随机变量下的需求与供应相平衡的库存模型。为此，本文需在分析供应商的订货量模型（Order Quantity Model，OQM）逻辑的基础上，利用模糊随机数学方法，对EOQ模型进行扩展，建立需VMI的订货量模型。本文考虑的模型的逻辑如图3。由持有库存、单位持有费用等确定值和模糊随机需求、准时到货率等参数确定订货量；以最小库存费用为目标，约束为资金和库存容量限制。

模糊随机环境下的定期订货、不允许缺货的VMI模型的存储状态图如图4。[T0，T+T0]为一个存储周期，也是采购量的消耗周期。T0时刻结束生产并运到仓库；T0时刻库存量迅速增加至最大存储量B2，并停止生产及运送；[T0，T+T0]时间内以存储满足需求，存储以速度r軇'减少。至T+T0时刻存储降为最低，进入下一个存储周期。

易知，在[T0，T+T0]时间内，T时段内的总费用包括供应商每次订货的订货费、生产准备、生产、配送及存储费用。设订货费、生产准备费、生产及配送费用之和为c1。单位产品的存储成本为h，平均存储量为故存储费为故[T0，T+T0]时间内总费用为：

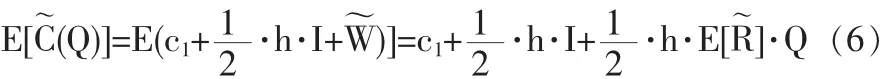
决策目的是寻找最优订货量Q，使得供应商的费用期望值达到极小。因此目标函数为：

假设在月初订货，已知I后，决策者确定订货量Q。根据Liu Y和Liu B（2003）[12]的定理，由于i（i=1,2,…，T+L）为模糊随机变量并且有有限期望值。若对每个ω∈Ω，各模糊变量i（ω）（i=1,2,…，T+L）相互独立，则理想状态下的公式为：

从图4可见，订货提前期为[0，T0]，存储量应恰好满足这段时间的需求，故定期检查库存量，当时不补充，当时补充。上式变为如下约束，即

假设B1为每周期最大的资金约束。如果决策者希望VMI下产品供应商每次的订货成本、生产准备、生产、配送成本与供应商的库存持有成本之和不超过可得到的每周期成本之和，则关于资金预算的约束为：

如果决策者希望定期检查时仓库的实际库存量与到货量之和不超过最大库存，则关于最大库存量的约束如下：

关于决策变量的非负约束为：

构造下列VMI的模糊随机期望值模型。

即：

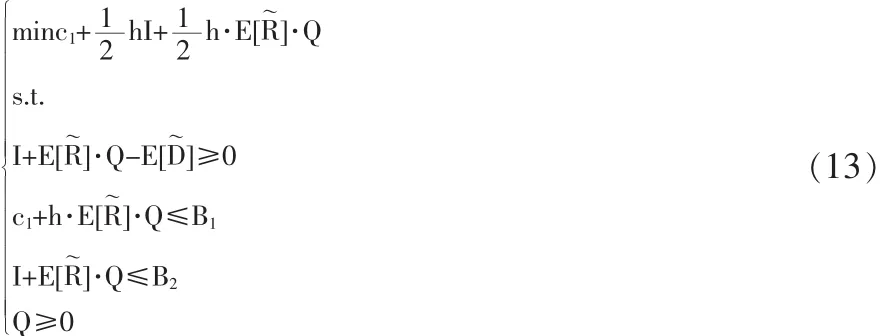
4 模型的求解

如果假设VMI模式下，供应商估计的下游企业的一个周期内总需求为，其中ρ1为正态随机变量，记为ρ1～N(a,σ2)，ρ1的概率密度函数为∞

表1 VM I库存系统参数值

可分析供应商的费用随库存管理费用变化的情况。具体方法为：将Q的值固定，将、I和Q的值代入（6）式并化简，得的表达式。由约束2（即（9）式）得h的取值范围。由于是关于h的函数，可作图表示当Q取某特定值时，供应商的费用随h变化的情况。还可将视h为变量，将E、c1、I、B1和B2的值代入（13）式。由约束1、3和约束4，得到Q的范围，作图分析供应商的费用随h和Q变化的情形。通过分析供应商的存储系统总费用随库存管理费用变化的情况，为企业决策最优订货量提供更进一步的依据。图5为假设Q=3700时的供应商的费用随变化的情况。图6为供应商的费用随h、Q变化的情况。

当模糊随机需求中的d1,d2,…，dn的隶属函数复杂，并且随机市场情形因素服从某种概率分布时，难以用解析方法求解该复杂模型。这时可利用模糊随机模拟与智能算法相结合的办法求解。

5 结论

目前VMI模式在制造业、燃料流通业、零售业等诸多行业中普遍存在。VMI中存在着大量的模糊随机不确定性。在经典的经济订购批量问题中，假设需求是一个确定数，并且假设当存储降为零时，可以立即得到补充并且所要补充的数量全部同时到位。而在这些行业中，需要研究定期订货、ADI和准时到货率为模糊随机变量、一次性到货的订货量模型。因此针对VMI应用中遇到的具体难题，本文将需求量、准时到货率变量刻画为模糊随机变量，以更真实而准确地反映企业现实环境，考虑需求与供给的平衡，将传统EOQ模型进行了扩展，使得库存控制理论的应用范围更广、适用性更强。对特殊情形得出了模型的解析解，讨论了供应商的库存费用随单位库存持有费用及订货量变化的情形，为企业决策最优订货量提供更进一步的依据。

[1]Tyan J,Wee Hui-Ming.Vendor Managed Inventory:a Survey of the Taiwanese Grocery Industry[J].Journal of Purchasing and supply Management,2003,(9).

[2]Liu Y K,Liu B.Fuzzy Random Variables:a Scalar Expected Value Operator[J].Fuzzy Optimization and Decision Making,2003,2(2).

[3]Liu B,Liu Y.Expected Value of Fuzzy Variables and Fuzzy Expected Value Models[J].IEEE Transactions Fuzzy Systems,2002,10(4).

[4]Liu B.Uncertainty Theory:an Introduction to its Axiomatic Foundations[M].Berlin：Springer-Verlag,2004.

[5]Das K.,Roy T.,Maiti M.Multi-item Stochastic and Fuzzy-stochastic Inventory Models under Two Restrictions[J].Computers&Operations Research,2004,（31）.

F224

A

1002－6487（2011）07－0058-04

李丽（1968-），女，山东德州人，博士，教授，研究方向：供应链管理、信息管理与信息系统。

(责任编辑/易永生)