SSSC在互联电力系统负荷频率控制中的应用
2011-10-30吴政球邹贤求王国民葛建伟
吴政球, 邹贤求, 陈 波, 王国民, 葛建伟
(湖南大学电气与信息工程学院, 长沙 410082)
SSSC在互联电力系统负荷频率控制中的应用
吴政球, 邹贤求, 陈 波, 王国民, 葛建伟
(湖南大学电气与信息工程学院, 长沙 410082)
建立了两区互联电力系统模型,分析了静止同步串联补偿器(SSSC)负荷频率控制的原理。SSSC频率控制器采用一阶控制环节,并通过超前滞后补偿进行校正。对两区互联系统线性化处理推出系统的状态方程,利用重叠分解对系统进行解耦求得控制系统阻尼比来设计SSSC频率控制器的目标函数,并通过改进遗传算法对控制器参数进行优化。仿真结果验证了采用SSSC频率控制器对减少频率波动的峰值和抑制区间低频振荡的有效性。
静止同步串联补偿器; 互联电力系统; 重叠分解; 负荷频率控制; 遗传算法
电网互联可以更有效地发挥大电网的优势,取得更好的经济效益,是电网发展的趋势[1]。然而互联电网使整个电力系统的动态过程变得更为复杂,给电力系统的控制带来一些困难,其中互联电力系统的频率稳定是研讨的重要问题之一。传统的负荷频率控制LFC(load frequency control)设备,如调速器等,因为其延时性,有时不能及时补偿负荷扰动,不能对电力系统频率进行有效控制,且电力系统的互联还可能导致电力系统的安全稳定裕度变少,诱发区域间的低频振荡。
随着柔性交流输电技术FACTS(flexible AC transmission systems)的迅速发展,大量的FACTS装置被广泛应用于电力系统中[2~6]。静止同步串联补偿器SSSC(static synchronous series compensator)是FACTS装置中的重要成员,与传统可控串联补偿设备相比,SSSC具有响应速度快、输出谐波含量小、避免谐振等优点[7~9],因此在电力系统中具有广阔的应用前景。SSSC具有优良的有功、无功解耦性能[10],既可以对交流系统补偿无功功率,也可以补偿有功功率,这意味着可以对SSSC的有功解耦进行控制,参与系统频率的控制。
本文在两区互联电力系统间安装SSSC装置参与系统频率的控制,充分利用SSSC快速响应、优良的有功解耦控制能力、不易产生谐振、安装灵活等优点。为了提高系统对负荷扰动的快速反应,对SSSC进行了解耦有功控制,利用SSSC响应速度快的特点,使系统更为迅速地调节输出功率平衡负荷扰动,减少频率波动峰值;其次,为了抑制互联电力系统区域间的低频振荡,设计了基于SSSC的频率控制器,并通过改进的遗传算法寻找最优参数,有效提高系统的低频阻尼能力。仿真结果验证了采用SSSC频率控制器的有效性。
1 SSSC频率控制器的数学原理
图1显示了连接了SSSC的两区互联电力系统模型,假设区域1主调频厂调整容量不足,而区域2调整容量大于本区域所需调整容量,可以通过联络线向其他区域传输功率。

图1 装有SSSC的两区互联电力系统
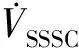
(1)
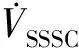
(2)

(3)



(4)


(5)
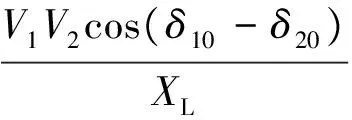
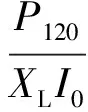
(6)
式中:下标尾数含0的量表示该变量的初始值。SSSC可通过控制电压变化量来控制输出有功功率的变化量,即
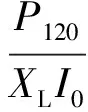
(7)
据此可知,SSSC可以对其有功功率进行解耦控制。将式(6)写成
ΔP12=ΔPT12+ΔPSSSC
(8)

T12(Δδ1-Δδ2)
式中,T12为区域1和区域2之间联络线功率同步系数。
2 SSSC频率控制器的设计
2.1 线性系统模型
SSSC频率控制采用一阶控制环节(TSSSC=0.03s ),并通过超前/滞后补偿对控制系统进行校正。SSSC频率控制器以区域1的频率变化量Δf1为输入量,采用负反馈闭环控制策略,则有
ΔuSSSC=-KSSSC(s)Δf1
(9)
超前滞后补偿环节为

(10)
式中:k为控制器系数,Tw为Washout滤波器时间常数,取Tw=10 s,T1~T4为时间常数。Washout滤波器可以去除稳态输入信号,使控制器环节只对动态信号响应。
图2为线性化的不含调速器[12]的两区电力系统模型,忽略时间常数TSSSC,系统状态方程为
(11)
其中,
B=[-1/M10a12/M2]T
Δx=[Δf1ΔPT12Δf2]T
式中:Δfi的区域i为频率差;ΔPT12为区域1和2的联络线功率变化量;Mi为区域i的惯性常数;Di为区域i的阻尼系数;a12为区域功率容量比。

图2 不含调速器线性化两区互联系统模型
2.2 重叠分解
重叠分解可对系统进行解耦分解,降低系统的阶数。取ΔPT12为重叠分量,则式(11)可写为
(12)
则可将两区系统分解为两个相关的子系统为
(13)
(14)
根据文献[13],如果每个解耦子系统可通过控制其输入,使各重叠子系统保持稳定,则可以保证原系统是稳定的。因此,可把式(13)和(14)互联系统S1和S2之间相互影响看作扰动,在控制器设计中可以忽略,只考虑系统其他输入作用,则解耦子系统可看作等式右边括号内的部分。因为系统只有一个输入ΔPSSSC,且位于子系统S1中,固选择解耦子系统S1作为分析设计系统。在系统S1引入SSSC控制器的时间常数TSSSC,得状态方程为
(15)
2.3 控制器目标函数
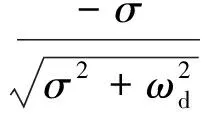
(16)
它决定了振荡幅值的衰减率和衰减特性。为了提高系统的阻尼特性,把控制器的目标函数设计为
F=min|ξa-ξd|
(17)
约束条件为
kmin≤kmax;Ti,min≤Ti≤Ti,max;i=1,…,4
式中:kmax、kmin分别为控制器系数增益取值的最大值和最小值;Ti,max、Ti,min分别为第i个时间常数取值的上下限;ξa为系统的实际阻尼比;ξb为控制系统的理想阻尼比。kmax、kmin分别取值为5、0.1;Ti,max、Ti,min分别取值为2和0.01。文中将通过改进遗传算法对SSSC频率控制器参数进行优化选择。
2.4 遗传算法(GA)对参数进行优化选择
GA是基于自然遗传学机理的随机优化概率搜索算法,适用于处理传统搜索方法难以解决的复杂和非线性问题。GA具有全局性、并行性、较好的适应性和鲁棒性,已在电力系统各领域得到了广泛的应用[14]。但基本GA存在易早熟和收敛速度慢的缺陷,因此,本文参考文献[15]中的最佳保留选择机制和文献[16]中自适应交叉和变异方法对遗传算法进行改进来求取最优参数,得出用于SSSC控制器参数优化的遗传算法流程如图3所示。

图3 改进遗传算法流程
3 仿真分析
采用如图4所示的两区域互联电力系统模型进行仿真,对SSSC的频率控制效果进行分析。

图4 仿真系统模型
系统在不同的扰动情况下,分别对不采用SSSC频率控制器和采用SSSC频率控制器的频率控制效果进行比较,见图5~7。在仿真系统中,采用两种扰动方式:①区域1在2 s时突然增加0.05 p.u.(标幺值)恒定有功负荷;②对区域1增加如图5所示的白噪音来模拟连续随机负荷扰动。

图5 白噪音扰动
取ξd=0.3,通过改进GA算法求得SSSC频率控制器参数如表1所示。

表1 SSSC频率控制器参数

(a) 区域1的频率偏差响应

(b) 区域2的频率偏差响应

(c) 区域1和区域2间联络线功率变化响应
图6显示了在扰动方式(1)情况下,两区域的频率偏差变化响应。从图6(a)、(b)可以看出,系统在没有SSSC频率控制器时,区域1和2频率下降幅度较大,且频率恢复过程都会产生振荡。而采用SSSC控制器后,频率波动的峰值明显减少,频率振荡得到明显抑制。
图6(c)为联络线传输的功率变化量,互联系统在采用SSSC频率控制器时,区域1和2之间的联络线功率的传输明显比不采用SSSC控制器时稳定,提高了联络线功率传送效率。SSSC频率控制器有功功率的迅速注入,使区域1频率波动峰值减少,因而引起联络线上瞬时传输的有功功率的峰值减少,同时也减少了因联络线突然传输功率向区域1给区域2电力系统带来的影响。
图7显示了在扰动方式(2)情况下两区域频率响应。可以看出采用SSSC控制时,频率波动峰值明显减少,频率控制效果得到明显改善。

(a) 区域1的频率偏差响应

(b) 区域2的频率偏差响应
4 结语
本文采用SSSC对互联电力系统进行负荷频率控制,分析了SSSC可以有功解耦进行频率控制的原理,通过对线性化两区系统和重叠分解解耦系统求得阻尼比建立SSSC频率控制器设计目标函数,并通过改进遗传算法求得控制器参数。算例系统表明,该频率控制器不仅可以充分利用SSSC快速反应的特点,更为快速地对负荷波动进行响应,有效抑制频率波动峰值,还可以提高系统阻尼阻尼特性,有效抑制互联系统区间低频振荡,提高了输电线路的输送能力和电力系统的稳定性、可靠性。
[1] 樊福而(Fan Fu′er).大电网互联系统的频率与潮流问题(Frequency and power flow of interconnected large power system)[J].电网技术(Power System Technology),2000,24(6):27-30.
[2] 陈礼义,曾颖,李林川,等(Chen Liyi,Zeng Ying,Li Linchuan,etal).具有FACTS设备的输电网络规划(Transmission network planning with FACTS devices based on modified adaptive genetic algorithm)[J].中国电机工程学报(Proceedings of the CSEE),1999,19(1):6-9.
[3] 蔡泽详,申洪,王荔(Cai Zexiang,Shen Hong,Wang Li).具有FACTS控制的EEAC法暂态稳定分析(The transient stability analysis based on EEAC including FACTS controllers)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2000,12(1):45-48.
[4] 王野平,武志刚,张尧(Wang Yeping,Wu Zhigang,Zhang Yao). FACTS设备在粤港电力系统中的潮流控制作用研究(Study of FACTS devices on power flow control in the Guangdong-Hong Kong power grid)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2002,14(4):76-79.
[5] 苏建设,柯宁,陈陈(Su Jianshe,Ke Ning,Chen Chen).提高暂态稳定的励磁与FACTS协调策略设计(Coordinated design of generator excitation and FACTS for transient stability enhancement)[J].中国电机工程学报(Proceedings of the CSEE),2003,23(9):6-10.
[6] 王成山,冯丽,吉兴全(Wang Chengshan,Feng Li,Ji Xingquan). 包含FACTS设备的输电网投资规划的博弈论分析(Game theory analysis of transmission expansion including FACTS devices)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2004,16(5):26-31.
[7] 颜伟,吴文胜,华智明,等(Yan Wei,Wu Wensheng,Hua Zhiming,etal).SSSC非线性控制的直接反馈线性化方法(Direct feedback linerization method for designing SSSC nonlinear control law)[J].中国电机工程学报(Proceedings of the CSEE),2003,23(3):65-68.
[8] 赵建军,郭剑波,周孝信(Zhao Jianjun,Guo Jianbo,Zhou Xiaoxin).静止同步串联补偿器变参数非线性暂态稳定控制器的设计(Design of transient stability controller of static synchronous series compensator based on variable parameters nonlinear control)[J].电网技术(Power System Technology),2005,29(21):14-20.
[9] 刘黎明,康勇,陈坚,等(Liu Liming,Kang Yong,Chen Jian,etal). SSSC建模、控制策略及性能(Static synchronous series compensator: modeling, control scheme and performance)[J].电工技术学报(Transactions of China Electrotechnical Society),2006,21(9):37-43.
[10]李胜,张建华,蒋程,等(Li Sheng,Zhang Jianhua,Jiang Cheng,etal).SSSC的有功和无功解耦策略(Active and reactive power flow decoupling method for SSSC)[J].电力系统保护与控制(Power System Protection and Control),2009,37(12):20-22,31.
[11]何仰赞,温增银.电力系统分析[M].武汉:华中科技大学出版社,2001.
[12]Elgerd O L. Electric Eenergy System Theory And Introduction[M]. New York: McGraw-Hill,1985.
[13]Ikeda M, Siljak D D, White D E. Decentralized control with overlapping information sets[J]. Journal of Optimization Theory and Applications,1981,34(2):279-310.
[14]黄开胜,童怀,郑泰胜,等(Huang Kaisheng,Tong Huai,Zheng Taisheng,etal).遗传算法在异步电动机动态模型参数识别中的应用(Parameters estimation for an induction motor's dynamic model using genetic algorithms)[J].中国电机工程学报(Proceedings of the CSEE) ,2000,20(8):37-41,55.
[15]陈国良,王煦法,庄镇泉,等.遗传算法及其应用[M].北京:人民邮电出版社,2001.
[16]王小平,曹立明.遗传算法—理论、应用与软件实现[M].西安:西安交通大学出版社,2002.
ApplicationofSSSCintheLoadFrequencyControlofInterconnectedPowerSystem
WU Zheng-qiu, ZOU Xian-qiu, CHEN Bo, WANG Guo-min, GE Jian-wei
(College of Electrical and Information Engineering, Hunan University, Changsha 410082, China)
A model of two-area interconnected power system is established to analyse the theory of static synchronous series compensator (SSSC) in load frequency control. The SSSC frequency controller uses a first-order controller, which is equipped with a lead-lag compensator. The state equation of system is derived based on the linear processing of the two-area system. By using overlapping decomposition to decouple the control system to obtain the damping ratio of the control system, the objective function of the SSSC frequency controller can be designed. Then the controller parameters are optimized by using the improved genetic algorithm. The good performance of the system obtained from simulation demonstrates that the SSSC frequency controller can not only reduce the peak of frequency fluctuation, but also can damp out inter-area low-frequency oscillation efficiently.
static synchronous series compensator(SSSC); interconnected power system; overlapping decomposition; load frequency control; genetic algorithm
2010-02-23;
2010-05-05
TM712; TM761
A
1003-8930(2011)05-0075-05
吴政球(1963-),男,博士,教授,博士生导师,研究方向为电力系统分析与控制、电力市场以及分布式发电及其并网等理论研究与工程实践。Email:zhengqiuwu@163.com 邹贤求(1985-),男,硕士研究生,研究方向为电力系统稳定与风电并网。Email:xianqiu0921@163.com 陈 波(1986-),男,硕士研究生,研究方向为风力发电及其并网技术。Email:chenbo198606@163.com
