20 kV电压等级经济性比较论证

程 杰， 向铁元， 张 贺， 李 敏

(1.武汉大学电气工程学院， 武汉 430072； 2.湖北省电力勘测设计院， 武汉 430024； 3.国网电力科学研究院， 武汉 430074)

20kV电压等级经济性比较论证

程 杰1，2， 向铁元1， 张 贺1， 李 敏3

(1.武汉大学电气工程学院， 武汉 430072； 2.湖北省电力勘测设计院， 武汉 430024； 3.国网电力科学研究院， 武汉 430074)

为研究20 kV电压等级的技术经济特性，在均匀负荷密度下建立数学模型，采用年总费用法分别对220/110/10 kV、220/110/20 kV、220/110/35 kV、220/35/10 kV、220/20 kV、220/35 kV这6种变电层次进行分析，得出年总费用法的目标函数和约束条件，并利用罚函数法解决此非线性规划问题。根据计算的结果对各种变电层次的经济性进行比较和分析，得出了20 kV电压等级在经济上的优越性，给出了各种方案不同负荷密度下中压的经济供电容量和经济供电半径。

20 kV； 经济性； 年总费用法； 比较； 论证

20 kV配电网的实施和应用在国外许多发达国家的城市和地区都已进行多年，从20世纪80年代开始就有学者进行这方面的研究，也提出过一些配电网最优供电模型的思路和方法[1～3]，综合起来有以下几种：

(1)在模型形状的选择方面，文献[1]和文献[2]采用圆型模型，文献[4]选择的是正六边形模型。圆形的负荷模型在计算和比较方面相对容易，但是由于受圆形几何特性的限制，圆形模型在平面上存在覆盖不到的区域，正六边形的模型比较贴合实际，但是计算相对复杂。

(2)在回路数选择方面，有固定回路数和根据负荷密度变化调整回路数。采用固定回路数容易比较和计算，但不符合实际，出线回路数应随负荷密度的增大而增加。固定出线回路数忽视了负荷密度对出线回路数的影响，适用于负荷密度变化范围不大的情况；但对不同配电层次的配电系统进行全面的经济比较，其负荷密度的变化范围大，如果仍认为出线回路数固定不变则与实际配电网相差很大。

(3)在供电半径选择方面，有的模型使用变电站最大容量。在负荷密度一定的情况下使变电站容量达到最大，这样可以使变压器的供电半径达到最大，这种假设方式认为供电半径越大经济效益越大，但是实际上供电半径越大出线就会越多，线路的投资与供电半径的三次方成正比。虽然半径扩大减少了变电站的投资，但线路的投资成本和损耗也相应增加，要想达到整体的效益最优，最佳供电半径不一定是在变电站供电半径最大时得到，要根据不同的目标函数来确定最佳的供电半径。

1 供电物理模型的比较和选择

本文采用的模型兼顾电压等级及负荷密度两大因素，供电区域的数学模型采用圆形。220 kV变电站位于圆心(只考虑1个220 kV变电站，且不考虑一次侧联络)，回路数随负荷密度的变化而变化，最优供电半径随目标函数的优化而变化；且认为供电区域内负荷均匀分布，配电网呈辐射状结构。

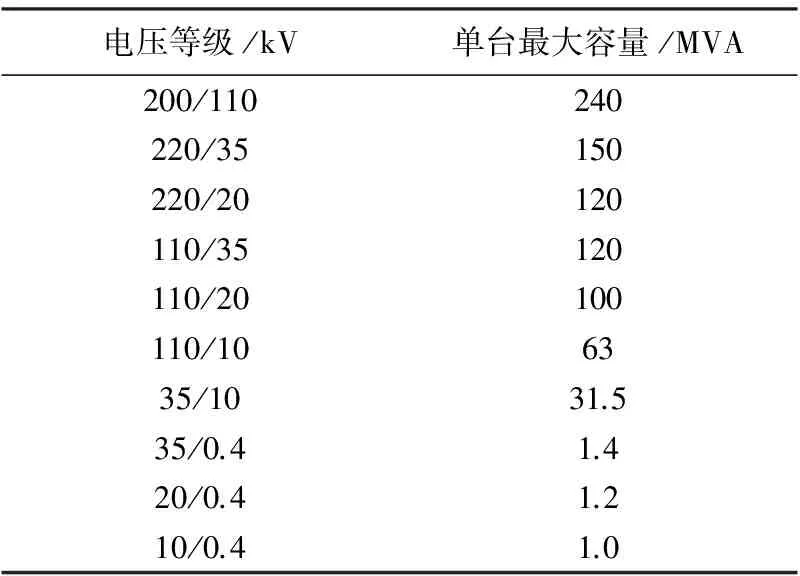
表1 单台主(配)变最大容量限制

在建立经济分析数学模型时，根据上述分析，作如下假设：

(1)各种变电等级的主变最大容量见表1。

(2)220 kV变电站供电区域为圆形，变电站位于圆心，在供电半径 的供电区域内，负荷密度为σ且分布均匀。

(3)电网呈辐射结构，且不同的电网接线方式相同(即在同一可靠性下)。

(4)根据《城市电力规划规范》110～220 kV变电站应选择2～4台主变，本经济模型选择3台，首要考虑横向备用，满足N-1准则，本模型中假设变压器运行率为2/3。

(5)导线的电流密度。对于电缆线路而言按照电缆安全载流量的一半选取。

(6)每回出线的平均负荷与电压成正比。

(7)各电压等级负荷功率因数取同一数值，在本模型中功率因数取0.95。

2 经济模型的建立

2.1 建设投资计算方法

在本模型中，引入变电站运行率kT，则有

kTScosφ=πR2σ

(1)

于是可得：

S=πR2σ/(kTcosφ)

(2)

式中：S为变电站主变总容量，MVA；R为变电站供电半径，km；σ为负荷密度，MW/km2。

根据文献[2]，对于变电站则有：

(1)变电站主干线导线总截面积AL为

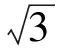
(3)

(2)出线的回路数M为

M=P/PL=Scosφ/PL

(4)

(3)每回配电出线的平均长度HL为

HL=DR

(5)

(4)变电站的建设投资I为

I=a1+b1S

(6)

(5)线路的投资IL为

IL=HL(a2M+b2AL)

(7)

式中：UN为配电网额定电压，kV；J为导线的经济电流密度，A/mm2；P为总负荷，MW；PL为每回线路的平均负荷，MW；cosφ为功率因数；D为线路曲折系数；a1为投资中与变电站容量无关的部分，万元；b1为投资中与变电站容量成线性关系的系数，万元/MVA；a2为投资中与导线截面无关部分的系数，万元；b2为投资中与导线截面成线性关系的系数，万元/mm2。

建设总投资包括5个部分：220 kV变电站的总投资、110 kV出线的建设总投资、110 kV变电站的建设总投资、中压(10 kV、20 kV、35 kV)线路建设总投资以及低压配电站建设总投资。下面将分别介绍各种投资的计算方法。

对于220/110/X(X=10、20、35)kV方案，设220 kV变电站的供电半径为R(km)，110 kV变电站供电半径为r(km)，XkV配变站供电半径为t(km)。设220 kV变电站的总投资I1，110 kV出线的建设总投资I2，每座110 kV变电站的建设投资I3、每条中压(10 kV、20 kV、35 kV)线路的建设投资I4，每座中压配电站建设投资I5，220/110/X(X=10、20、35)kV方案的总投资总额I6为

I6=I1+I2+(R/r)2(I3+I4)+(R/t)2I5

(8)

对于220/35/10 kV方案的投资计算可以参照上述方法。对于220/20 kV方案以及220/35 kV方案的投资计算方法为

(9)

2.2 损耗的计算方法

根据数学模型所作假设(1)和(2)，并受文献[2]启示，线路损耗可以采用如下方法计算。

设假定每回出线的供电范围为一扇形，如图所示，其圆心角θ为

θ=2π/M

(10)

半径为R，在距离变电站x处，导线电流i(kA)为

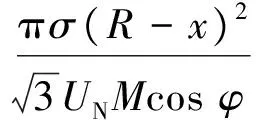
(11)

长度为dx线路上的电阻为ρdx/AL，则每回出线的功率损耗(MW)为

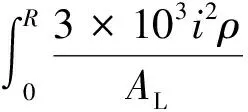
(12)

M条出线1年的总损耗(万元)为

(13)

式中：ρ为电阻率，Ω·m；τ为最大负荷损耗小时数，h；C0为损耗电价，元/(kW·h)。

对于一个变压器而言，损耗主要是铁耗ΔWFe和铜耗ΔWCu。设变压器额定容量为ST(kVA)，运行率为kT，年最大负荷损耗时间为τ(h)，空载损耗为ΔPT0(kW)，短路损耗为ΔPTk(kW)，则变压器年电能损耗ΔW(kW·h)为

ΔW=ΔWFe+ΔWCu=

(14)

式中，kZ为综合考虑了变压器的铜耗和铁耗之后的等效损耗系数，选取了各种不同变压等级目前使用较广泛型号的变压器经过回归分析后得到的等效系数。

kZ=8 760k′+k″(kT)2τ

(15)

式中，k′和k″分别为变压器的铁耗和铜耗折算系数。

设220 kV变电站的年损耗费用为L1，110 kV出线的年损耗费用为L2，每座110 kV变电站的建设投资L3及其每条中压出线的年损耗费用L4，每座低压配电站年损耗费用L5。

220/110/X(X=10、20、35)kV方案的年损耗费用总额L6为

L6=L1+L2+(R/r)2(L3+L4)+(R/t)2L5

(16)

另外220/35/10 kV方案的年损耗费用计算可以参照上述方法。对于220/20 kV方案或220/35 kV方案的年损耗费用计算方法为

(17)

3 目标函数建立和求解

本经济比较的目标函数为：单位负荷的年总费用最小。

以I6表示方案的总投资，u表示等年值年运行费用，n为方案的服务年限，i为折现率。在评价方案中，年总费用最小的方案其经济效益最大，应该作为决策方案，单位负荷年总费用的计算式为

(18)

式中：q为资金回收系数，q=i(1+i)n/[(1+i)n-1]；u为等值年运行费用，它包括年电能损耗费用L6和年运行维护费用I7(按总投资I6的一定比例提取，即u=L6+I7=I6+kYI6，提取比例kY按照国家相关财务法规选取为1.5%)，则目标函数表示为

F=[(q+kY)I6+L6]/πR2σ

(19)

将式(1)～式(17)代入式(19)中经过整理后可得

F=c1R-2+c2R-1/2+c3R+e1r-2+

e2r-1/2+e3r+f1t-2+f2t-1/2+f3t

(20)

其中c1、c2、c3、e1、e2、e3、f1、f2、f3为含有负荷密度σ的函数，当负荷密度一定时，它们都为常数。对于两级电压层次的方案(220/35 kV方案以及220/20 kV方案)的目标函数可以参照上述求法进行求解，在此不再赘述。式(20)的约束条件如下。

(1)220 kV变电站容量限制为

S220=πR2σ/(kTcosφ)≤S220max

(21)

(2)110 kV变电站容量限制为

S110=πr2σ/(kTcosφ)≤S110max

(22)

(3)中压(10 kV、20 kV、35 kV)配电变电站容量限制为

SP=πt2σ/(kTcosφ)≤SPmax

(23)

(4)110 kV输电线的电压降限制为

(24)

(5)中压配电线路电压降限制(类比(4))；

(6)0.4 kV配电线路电压降限制(类比(4))。

在模型中近似认为110 kV电缆的电抗值为电阻值的3倍，35 kV、20 kV以及10 kV电缆的电抗值为电阻值的1/2，单台主变最大容量的选取如表1所示。

当不考虑约束条件时，可以使用拉格朗日求极值的方法求得式(20)的极值，当目标函数F取得最小值时，各变量的值分别为

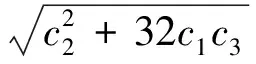
(25)

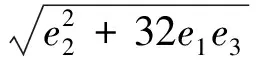
(26)

模型中与变电站相关的参数如表2所示，与线路相关的参数如表3所示[6，7，9，10]。线路均采用电缆线。

表2 变电站造价参数

表3 电缆线造价参数

4 结果及分析

考虑约束条件式(21)～式(24)时，目标函数式(20)是一个典型的带有约束条件的非线性规划问题，可采用罚函数法编制计算机程序进行优化求解，求得的结果见图1和图2所示：

从图1可以看出：220/20 kV方案的年运行费用最小，220/35 kV方案的年运行费用其次，接着是220/110/20 kV方案、220/110/35 kV方案和220/110/10 kV方案，最差的是220/35/10 kV方案。

但是35 kV如果直接降压至0.4 kV，则配变的容量不能过大，否则其低压侧的短路电流将超过断路器的遮断容量的限值。经测算，只有当35 kV配变的容量被限制在1.4 MVA以下时，0.4 kV侧的短路电流才会被限制在30 kA以下。短路电流过大，在技术上可以通过装设高阻抗变压器，否则，须将35 kV先降至10 kV，这样220/35 kV方案就会变成220/35/10 kV方案，而此种方案的年总费用是最大的。而装设高阻抗变压器，但这样会增大变压器损耗和变压器的制造成本，故不可取。

图1 各方案年总费用比较

本文利用年总费用法进行经济分析和评价得出220/20 kV方案单位负荷年费用最少，220/110/20 kV电压序列能够适应目前110 kV网架大量存在的实际情况，且综合优势仅次于220/20 kV方案，两者结合利用相得益彰。对于110 kV网架结构比较完善的地区，推荐使用220/110/20 kV电压等级序列。这样可以充分利用现有网架结构，节省投资，提高经济效益，为建立资源节约型、环境友好性社会创造基本条件。

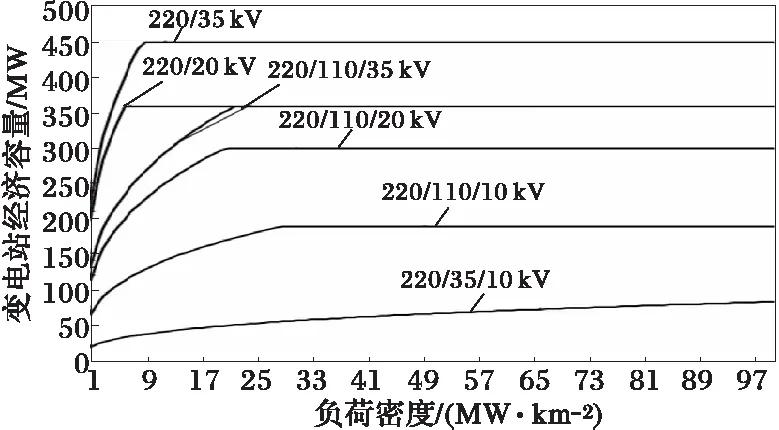
图2 各方案变电站中压经济容量比较

从图2中可以看出：各方案变电站的经济供电容量达到容量上限时所对应的负荷密度分别为：220/110/10 kV：30 MW/km2；220/110/20 kV：21 MW/km2；220/110/35 kV：22 MW/km2；220/20 kV：8 MW/km2；220/35 kV：10 MW/km2；220/35/10 kV在负荷密度为100 MW/km2时仍未达到变电站容量上限。在达到上限以前以经济供电容量来确定供电范围，单位负荷年总费用最少，经济性最好。

220 kV和110 kV变电站在未达到容量上限时，经济供电半径Rmin和rmin可以用式(25)和式(26)进行计算；在达到容量上限时以变电站总额定容量供电经济性最好，对应的经济供电半径可采用变电站容量上限Smax利用式(1)进行计算，即

Rmin=(kTSmaxcosφ/π/σ)1/2

(27)

从计算结果看，220/20 kV方案的单位负荷年总费用最少，是最优方案。

5 结语

本文采用年总费用法来研究6种电压等级的经济性。首先建立数学模型，得出年总费用的目标函数，并采用罚函数法来求解目标函数，然后结合具体的技术经济参数进行计算，并根据计算结果分析得出220 kV直降20 kV的经济性最好。

法国巴黎电网应用220 kV直降20 kV模式在已经多年(1960年至今)，并将380/225/20/0.4 kV作为标准降压层级，经过多年运行，技术上和实际运行上都可行，为国内开展和实施与220/20 kV电压等级相关工作的提供了一些参考和借鉴。我国南方某特区城市进行电网规划时选择了220/20 kV方案作为实施方案。采用这一方案可以取得很好的经济效益，不仅投资少，而且还能减少电压层级，降低电网损耗。目前该地区正在进行试点，试点成功后可以为其他地区开展电压层级优化工作提供经验和借鉴，以便在全国其他地区推广应用。

[1] 于永源,王贤正,杨绮雯(Yu Yongyuan, Wang Xianzheng, Yang Yiwen).变电所经济供电半径的优化选择(Optitionnal selection for substation feed economic radium)[J]. 电力科学与技术学报(Journal of Electric Power Science and Technology), 1991, 6(1): 118-124.

[2] 张秀然, 孙国凯, 朴在林,等(Zhang Xiuran, Sun Guokai, Piao Zailin,etal). 66/10kV配电线路经济供电半径的探讨(Economical radius of power supply for 66/10kV distribution line)[J].农村电气化(Rural Electrification),1997,19(11):4-6.

[3] 杨期余, 张仲力, 杨明志,等(Yang Qiyu, Zhang Zhongli, Yang Mingzhi,etal).城市电网规划中变电站容量的动态优化(The dynamic optimization of substation capacity in urban grid planning)[C]∥全国高等学校电力系统及其自动化专业第三届学术年会论文集(Collection of China Universities 3rd Annual Conference on Electric Power Systems and Automation ),西安: 1987.

[4] 原河峰, 刘连杰(Yuan Hefeng, Liu Lianjie). 对我国农村配电网最佳电压的研讨(The research of distribution voltage in rural area)[J].郑州大学学报：工学版(Journal of Zhengzhou University：Engineering Science), 1986,7(2):81-87.

[5] 范明天,张祖平.中国配电网发展战略相关问题研究[M]. 北京: 中国电力出版社,2008.

[6] Q/GDW 156-2006， 城市电力网规划设计导则[S].

[7] 刘振亚. 国家电网公司输变电工程典型造价 [M].北京: 中国电力出版社,2008.

[8] 曹炳元(Cao Bingyuan).经济供电半径的 Fuzzy几何规划模型与优选方法(Model of fuzzy geometric programming in economical power supply radius and optimum seeking method)[J]. 中国工程科学(Engineering Science), 2001, 3(3): 52-55,70.

[9] 20 kV电压等级配电技术论文集[M].北京:中国电力出版社,2008.

[10]吴夕科(Wu Xike).南方电网城市配网供电电压等级研究报告(Voltage grade study of urban distribution network in China southern power grid)[R]. 武汉: 武汉高压研究所(Wuhan: Wuhan High Voltage Research Institute),2005.

[11]郑正圻(Zheng Zhengqi).20 kV电压等级论证(20kV voltage grade study)[R]. 武汉: 武汉高压研究所(Wuhan: Wuhan High Voltage Research Institute),1994.

[12]温建春,韩学山,张利(Wen Jianchun, Han Xueshan, Zhang Li).一种配电网理论线损计算的改进算法(Improved method for theoretical line loss calculation of distribution network) [J].电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2008,20(4):72-76.

[13]彭新宇,黄民翔,许诺,等(Peng Xinyu, Huang Minxiang, Xu Nuo,etal).10 kV配电网线损的快速计算法 (Fast method of 10 kV power distribution network' s energy loss calculation)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2002,14(4):45-47.

ComparisonandDemonstrationontheEconomicalEfficiencyof20kVVoltageSeries

CHENG Jie1，2， XIANG Tie-yuan1， ZHANG He1， LI Min3

(1.School of Electrical Engineering, Wuhan University, Wuhan 430072, China； 2.Hubei Electric Power Survey & Design Institute, Wuhan 430024, China; 3.State Grid Electric Power Research Institute, Wuhan 430074, China)

In order to study the technical and economic characteristics of 20 kV, the mathematical model is established and the minimum annual expense method is used to analyze six types of transforming grades of 220/110/10 kV, 220/110/20 kV, 220/110/35 kV, 220/35/10 kV, 220/20 kV and 220/35 kV, and the target function and constraint condition for the annual total expenses method is deduced. Then the penalty method to solve the non-liner programming problem is adopted. In the end, the economical efficiency for every scheme are analyzed and compared, and the conclusion shows that the 20 kV is the best scheme among, and the economical power supply capacity and economic power supply radius of middle voltage for every scheme are obtained.

20 kV； economic efficiency； annual total expenses method； comparison； demonstration

2010-01-14；

2010-04-21

TM715

A

1003-8930(2011)05-0125-06

程 杰(1983-)，男，硕士研究生，研究方向为电力系统运行与控制。Email:jkchengjie@163.com 向铁元(1953-)，男，教授，博士生导师，研究方向为电力系统运行与控制。Email:xty01@163.com 张 贺(1985-)，男，硕士研究生，研究方向为电力系统运行与控制。Email:zhanghe@163.com