模糊数学法在学生成绩评价中的应用
2011-10-30魏永义赵永敢
魏永义,赵永敢,王 飞
(漯河医学高等专科学校,河南 漯河 462002)
模糊数学法在学生成绩评价中的应用
魏永义,赵永敢,王 飞
(漯河医学高等专科学校,河南 漯河 462002)
模糊数学法;学生成绩;综合评价
食品理化检验技术教学评价是高职高专食品专业教学过程的重要环节,是评定学生学习成绩和检验教师教学效果的重要手段,同时也是促进教学改革、加强教学管理和提高教学质量的重要途径和基本手段。它对学生的学习活动具有一定的导向作用[1],还有利于加强学生学习的主动性。
模糊数学法是应用模糊数学的有关理论,对多因素的制约关系进行数学化的抽象,建立一个反映其本质特征和动态过程的理想化评价模式[2]。模糊数学评判方法较适宜于评价因素多、结构层次多的对象系统[3],在学生成绩评价方面也得到了广泛的应用[4~5]。
目前,学生成绩评价受到很多因素的制约,很难得到一个确切的评价结果。因此,笔者采用模糊数学法对食品理化检验技术课程的学生成绩进行了综合评价,主要是为学生成绩的评定提供一种比较客观、科学、有效的方法,从而为正确评价学生成绩提供理论依据。
1 模糊数学方法的建立
1.1 评价方法
由5名评价人员组成评定小组,对学生的期末考试成绩、实验成绩、平时成绩3个因素(见表1)进行评定,并分设5个等级,即优、良、中、合格和不合格,要求评定人员客观地进行评价。全部评价结束后,收集评定人员的评定表,进行统计分析。

表1 评价因素及其权重分配情况
1.2 模糊数学模型的建立
以期末考试成绩、实验成绩、平时成绩为一级因素集,二级因素集见表1,以优、良、中、合格和不合格为评语集,根据学生成绩评定结果,建立一级因素和二级因素评价矩阵,用模糊数学评价方法对其进行分析。
1.2.1 学生成绩的因素集、评语集 因素集U={期末考试成绩(u1),实验成绩(u2),平时成绩(u3)},其中ui(i=1,2,……,n)为第i个因素子集,二级因素集见表1。评语集V={v1优,v2良,v3中,v4合格,v5不合格},其中优(90分以上),良(80~90分),中(70~79分),合格(60~69分),不合格(60分以下)。
1.2.2 权重的确定 因素权重集 X={x1,x2,x3},其中 xi(i=1,2,……,n)为第i个权重子集,二级因素权重集见表1。
1.2.3 模糊关系综合评判集 模糊关系综合评判集Y=X·R,其中X为权重集,R为模糊矩阵。
2 学生成绩评定结果与分析
2.1 评定结果
5名评价人员按照制订的评定方法和标准对一位学生的食品理化检验技术成绩进行了评定,结果见表2。

表2 学生成绩评价结果
2.2 一级模糊综合评定
根据表1权重分配和表2中的评定结果计算一级模糊综合评定集。
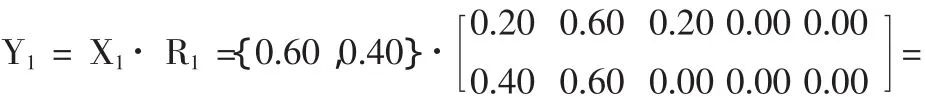

2.3 二级模糊综合评定

归一化后得 Y`=(0.33,0.50,0.17,0.00,0.00),得到模糊数学关系综合评判的峰值为0.50,与原假设相比,得出该学生的食品理化检验技术成绩综合评定级别为良(80~90分)。
3 结论
笔者采用模糊数学法对一位学生的食品理化检验技术成绩进行了评价,得出该学生的食品理化检验技术成绩的综合评定级别为良,该评价方法客观、公正,从而为学生成绩的正确评价提供了理论依据。
[1]高苗苗,田金华.对高校体操教学中学生成绩评价的探讨[J].山西大同大学学报(自然科学版),2008,24(5):91~93.
[2]张水华,徐树来,王永华.食品感官分析与实验[M].北京:化学工业出版社,2006.
[3]段立群.建立在模糊数学基础上的综合评估方法[J].煤炭技术,2008,10:138~140.
[4]尉强,杨启红.学生成绩评价的数学建模[J].洛阳师范学院学报,2006,5:124~126.
[5]谢敏玲.教学改革中学生成绩评价的数学模型[J].高等函授学报,2009,5:62~65.
G40-03
B
1671-1246(2011)08-0040-02
