数控加工中直线和圆弧的插补

罗娅 广东省交通运输高级技工学校

数控加工中直线和圆弧的插补

罗娅 广东省交通运输高级技工学校

在数控机床上要形成对工件几何轨迹的轮廓控制，必须使两坐标或两坐标以上行程信息的指令脉冲用适当方法进行分配，从而合成所需的运动轨迹。插补即为根据进给速度的要求，在零件轮廓的起点和终点之间计算出若干个在允许范围内的中间点的坐标值。由于每个中间点计算所需的时间直接影响系统的控制速度，而插补中间点坐标值的计算精度又直接影响到CNC系统（又称计算机数控系统）的控制精度，所以插补法是整个CNC系统控制的核心。我们应该让编制程序的学生掌握插补原理，清楚地知道在实际加工过程中，刀具的运动轨迹是折线，而不是光滑的曲线。刀具不能严格地沿着要求的曲线运动，只能沿折线逼近所要加工的曲线。

CNC;直线;圆弧;插补

引言

在数控机床上加工各种工件，工件轮廓大部分是由直线和圆弧这两种简单、基本的曲线构成，如果加工的轮廓是非圆曲线，也可以采用一小段直线或圆弧来拟合。数控系统是对执行机构进行控制从而得到几何轨迹轮廓，一般是已知工件轮廓的运动轨迹的起点坐标、终点坐标和轮廓轨迹的曲线方程，由数控系统算出各个中间点的坐标值，“插入”、“补上”运动轨迹中间点的坐标值，换言之，插补就是沿着规定的工件轮廓，在轮廓的起点和终点之间按一定的算法进行数据的密化。插补结果输出运动轨迹中间点的坐标值，数控机床伺服系统根据该坐标值控制各坐标轴协调运动，刀具走出预定轨迹。

一、CNC目前应用的插补法

（一）由插补输出的标量有：

1、数字脉冲增量法：以行程为标量，每来一个进给脉冲进行插补运算一次，相应有一个脉冲当量的位移输出。

2、数据采样法：以时间为标量，即在选定插补周期的时间后，按给定的进给值，在一个插补周期时间内输出相应的一小段步长数据（称粗插补），这一步长再通过对实际位置采样值比较的伺服位置控制进行细化插补（称精插补）输出。

（二）由插补的规则可有：

1、逐点比较法：每次插补进给只有一个坐标轴动作，且按判别、进给、偏差计算、终点判断进行。

2、数字积分法：利用寄存器长度的有限性把给定的行程数据进行数字微分分析累加，取累加寄存器的溢出脉冲作为进给输出脉冲。

3、比较积分法：直接比较各坐标轴的积分值，并把积分值在时间轴上看作一个时间间隔，然后利用逐点比较法的判别式引入一个判别函数，来判别各个坐标轴总的时间间隔差。

（三）由几何规律可有：直线插补和圆弧插补。

二、逐点比较插补法的四个工作节拍

（一）直线插补

1、位置判别。根据偏差符合，判断刀具当前位置与工件理想轮廓的相对位置，以便确定进给方向。偏差判别式为：F m=Y m X e-XmYe（Xe、Ye为加工轨迹的终点坐标，Xm、Ym为加工点即动点坐标）。

2、坐标进给。根据判别结果，控制某坐标台进给一步，向规定的轨迹靠拢，缩小偏差。例如第一象限直线：当Fm＞0时，向+X方向进给一步；Fm＜0时，向+Y方向进给一步；Fm=0时，为保证插补的连续进行，可向+X方向进给一步，也可以向+Y方向进给一步，本文规定向+X方向进给一步；如表1所示。

表2 直线插补计算过程

表1 直线进给插补计算公式及进给方向

注：表中L1、L2、L3、L4分别表示第Ⅰ、Ⅱ、Ⅲ、Ⅳ象限直线。

3、偏差计算。坐标进给一步后，计算新的加工点对规定轨迹的偏差，作为下一步偏差判别的依据。新加工点的偏差：Fm≥0时，Fm+1=Fm-Ye; Fm＜0时，Fm+1=Fm+Xe。

表5 直线插补计算过程

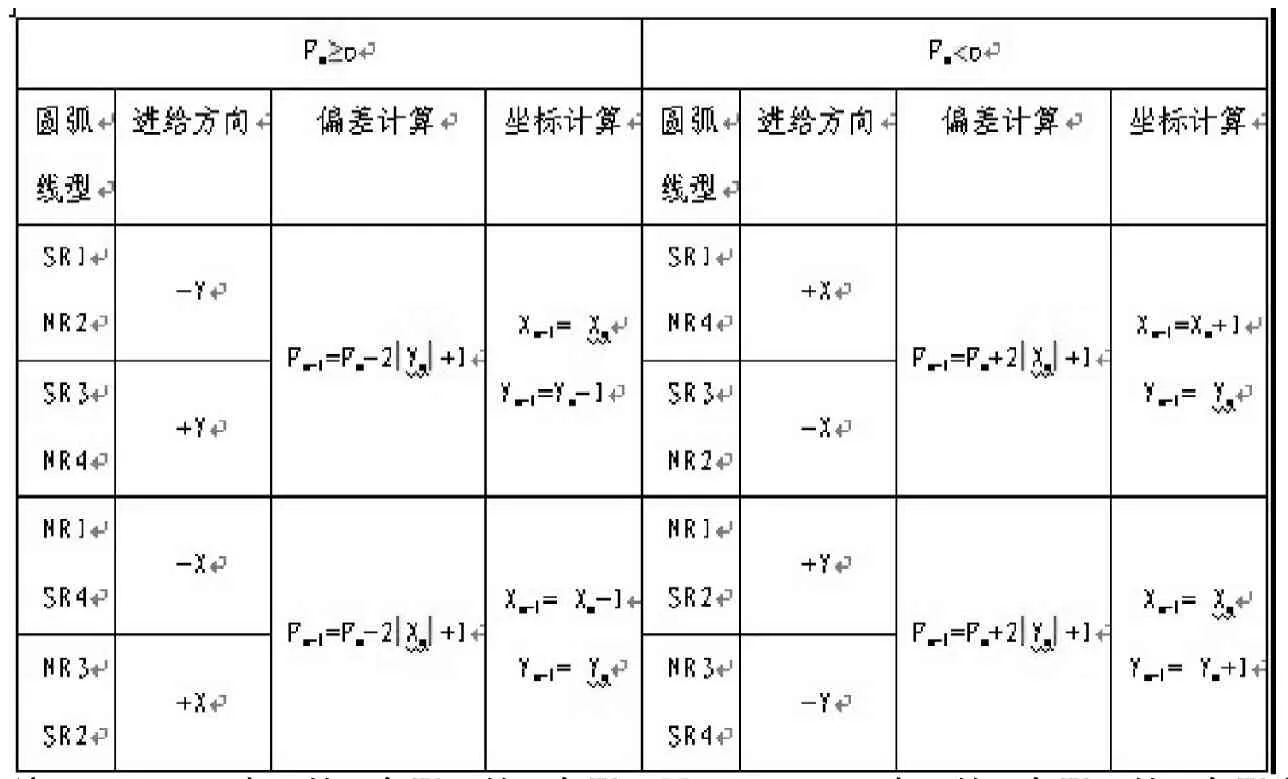
表3 圆弧插补计算公式和进给方向

4、终点判别。每进给一步，判断是否达到程序规定的加工终点。若到达终点，则停止插补，否则，继续插补。判别方法有两种：

（1）在终点计数器中存入X和Y两坐标进给的总步数N=Xe+Ye，当X或Y坐标进给时，N值逐步减1，直至N=0时停止插补。也可以设置两个计数器，在计数器中分别存入终点坐标Xe和Ye，X或Y方向每进给一步，就在相应的计数器中减1，直到两个计数器中的数都减为零时停止插补。

（2）在终点计数器中存入插补循环数i的初始值0和两坐标进给的总步数N，每进行一次插补循环即X或Y方向每进给一步，就在循环数i上加1，直到i=N时停止插补。

5、逐点比较法插补第二象限直线实例。直线起点为O（0,0），终点为E（-6,5），写出插补运算过程并绘出插补轨迹。

（1）加工完该段直线OE，刀具沿X、Y轴应进给的总步数为N=Xe+Ye=6+5=11。

（2）根据以上公式和图1，可得直线插补计算过程，如表2所示。

图1 不同象限直线插补偏差符号和进给方向

（3）插补轨迹图，如图2所示。

图2 直线插补轨迹

（二）圆弧插补

1、位置判别。例如第一象限的逆圆弧，当F m=0，表示动点在圆弧上；F m＞0时，表示动点在圆弧外， Fm＜0时，表示动点在圆弧内。

2、坐标进给。应使加工点逼近给定圆弧，如图3所示。

3、偏差计算。如表3所示。

4、终点判别。与直线插补终点判别的方法相同。

5、逐点比较法插补第一象限逆圆实例。

圆弧AB，起点A（5，0），终点B（0,5）。写出插补运算过程并绘出插补轨迹。

（1）加工完该圆弧，刀具沿X、Y轴应进给的总步数为N=Xe+Ye=5+5=10。

图3 四个象限圆弧插补偏差符号和进给方向

（2）根据以上公式和图3，可得圆弧插补计算过程，如表4所示。

（3）插补轨迹图，如图4所示。

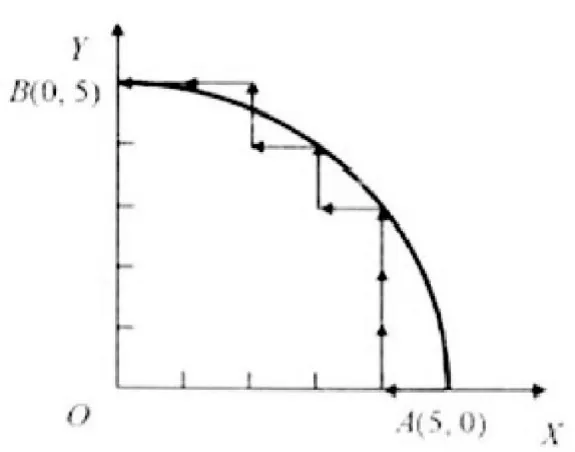
图4 圆弧插补轨迹

三、数字积分插补法

（一）数字积分法直线插补

1、工作原理

插补运算由两个数字积分器进行，每个坐标轴的积分器由累加器和被积函数寄存器组成。被积函数寄存器存放终点坐标，每来一个△t脉冲，被积函数寄存器里的函数值送往相应的累加器中相加一次。当累加和超过累加器的容量时，便溢出脉冲，作为驱动相应坐标轴的进给脉冲△X（或△Y），而余数仍存在累加器中。

2、终点判别。直线插补只需完成m=2n次累加运算，即可达到直线的终点，当计数器记满2n数时，插补停止。

3、数字积分法插补第一象限直线实例

直线起点为O（0,0），终点为A（10,5），累加器和寄存器的位数均为四位，写出插补运算过程并绘出插补轨迹。

（1）加工完该段直线O A，根据m=2n=24=16，插补累加次数为16。

（2）根据以上公式,可得直线插补计算过程，如表5所示。

（3）插补轨迹图，如图5所示。

图5 直线插补轨迹

（二）数字积分法圆弧插补

1、运算开始时，X轴和Y轴被积函数寄存器中分别存放X、Y的起点坐标值X0、Y0。累加过程中不断地修正被积函数寄存器中的坐标值。

2、X轴被积函数寄存器的数与其累加器的数累加得出的溢出脉冲发到+X或-X方向，而Y轴被积函数寄存器的数与其累加器的数累加得出的溢出脉冲发到+Y方向或-Y方向。

3、每发出一个进给脉冲后，必须将被积函数寄存器内的坐标值加以修正。当X方向发出进给脉冲时，使Y轴被积函数寄存器内容加或减1；当Y方向发出进给脉冲时，使X轴被积函数寄存器内容加或减1。即：圆弧插补时，被积函数寄存器内随时存放坐标的瞬时值；而直线插补时，被积函数寄存器内存放的是不变的终点坐标值Xe、Ye。

四、数据采样插补

随着数控技术的发展，以交流伺服为驱动元件的计算机闭环数字系统已成为数控系统的主流。采用这类伺服系统的数控系统，一般都采用数据采样插补法。该方法是根据编程的进给速度，将轮廓曲线分割为插补周期的进给步长，插补一般由粗、精插补两步完成。第一步粗插补，由它在给定曲线的起点、终点之间插入若干个中间点，将曲线分割成若干个微小直线段来逼近曲线；第二步在粗插补的基础上，由精插补进一步进行数据点的密化工作，进行对直线的脉冲增量插补。

表4 圆弧插补计算过程

五、三种插补法的优劣比较

1、逐点比较法运算直观，插补误差小于一个脉冲当量，因而只需将脉冲当量取得足够小就可达到加工精度的要求，输出脉冲均匀，调节方便。只是每控制机床坐标轴进给一步，都要完成四个工作节拍。适宜步进电机简易的两坐标数控机床。

2、数字积分法具有运算速度快、脉冲分配均匀、易实现多轴联动，不仅能方便地实现一次、二次曲线的插补，还可以用于各种函数运算，应用广泛。

3、数据采样插补法用于闭环伺服系统中，其输出的结果不是脉冲，而是数据，所产生的最大速度不受计算机最大运算速度的限制，但插补程序比较复杂。

在当今的职业教育过程中“以就业为导向，以服务为宗旨”，以“工学结合”为主线的教学思想应具体落实到每个细节中，要把数控加工编程的高技能人才培养成为，除具有良好的职业道德和职业素质以外，还应当有扎实的、系统的专业应用知识，走上工作岗位后具备持续发展的能力。本文把CNC中核心内容——插补原理，通过实例的应用让学生更加清晰的理解工件轮廓形成的原理，使之能“知其然，必知其所以然。”把系统的专业知识充分应用到工作岗位中。

[1]王宝成.数控机床与编程实用教程.天津：天津大学出版社.2004.1

[2]吴建蓉，王炜.数控加工技术与应用.福州：福建科学技术出版社.2005.9

[3]明兴祖.数控加工技术.北京：化学工业出版社.2003.10

[4]陈志雄.数控机床与数控编程技术.北京：化学工业出版社.2003.8

10.3969/j.issn.1001-8972.2011.13.063