我国固定资产投资总额的动态分析——基于AR IMA模型

○吴 雨 蔓朱胜（成都信息工程学院 四川 成都 610103）

我国固定资产投资总额的动态分析
——基于AR IMA模型

○吴 雨 蔓朱胜（成都信息工程学院 四川 成都 610103）

固定资产投资总额是影响一国经济增长的重要因素，对拉动国民经济的发展起着至关重要的作用。本文以我国固定资产投资总额为例，选取1982—2009年全社会固定资产投资总额的时间序列数据，利用Eviews软件对该数据进行计量分析，研究我国固定资产投资总额的变化趋势和特征，建立自回归移动平均模型即ARIMA模型，并据此模型对我国固定资产投资总额进行预测，分析未来投资规模趋势。

固定资产投资总额 时间序列 ARIMA模型

一、引言

我国固定资产投资政策对国民经济有着至关重要的影响。纵观改革开放30多年来我国经济增长的变动趋势，不难发现固定资产投资是影响其变动的主要因素。1981—1990年我国固定资产投资对经济增长的贡献份额为56.65%；1991—2002年固定资产投资对经济增长的贡献份额为64.85%。而同期劳动力对经济增长的贡献份额分别仅为26.22%、6.65%，科技进步对我国经济增长的贡献份额分别为17.13%、28.170%。可见，固定资产投资在推动我国经济高速发展的历程中有着不容忽视的作用。

固定资产投资是影响我国过去、当前及未来一段时期经济增长的关键因素。我国固定资产投资增势良好，对国民经济的平稳增长起到了重要的支撑作用，固定资产投资总额的变化对投资策略和经济增长研究具有一定的指导作用。因此，研究我国固定资产投资总额变化趋势具有必要性。本文通过对选取的数据建立自回归移动平均模型，对固定资产投资总额进行动态分析和预测，并对预测效果给予评价。

二、ARIMA建模思想与步骤

ARIMA（p，d，q）模型是美国统计学家Box和Jenkins于1970年首次提出的，广泛应用于各种类型时间序列数据的分析方法，是一种预测精度较高的短期预测方法。其实质是差分运算与ARMA模型的组合。

ARIMA模型的基本思想是：将预测对象随时间推移而形成的数据序列视为一个随机序列，用一定的数学模型来近似描述这个序列。这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值。现代统计方法、计量经济模型在某种程度上已经能够帮助企业对未来进行预测。其建模步骤主要为：第一，对序列的平稳性进行识别；第二，对非平稳序列进行平稳化处理；第三，建立相应的模型并对参数进行估计；第四，检验模型的估计效果；第五，利用模型进行预测分析。

三、ARIMA模型在固定资产投资中的应用

1、数据的选取

本文选取1982—2009年全社会固定资产投资年度总额进行建模，探讨模型在固定资产投资预测中的应用。数据来源于国家统计局网站的年度统计数据（具体数据略）。

2、数据的处理

（1）数据的时间序列趋势性

由于原始数据差异较大，为了便于有效分析固定资产投资总额变化趋势，消除时间序列的异方差性，对原数据取对数并将生成的新序列定义为LnY，运用EVIEWS软件对上述数据做趋势图，如图1所示。从图1可以明显看出，取对数后的固定资产投资总额时间序列随着时间的外后推移呈递增趋势。

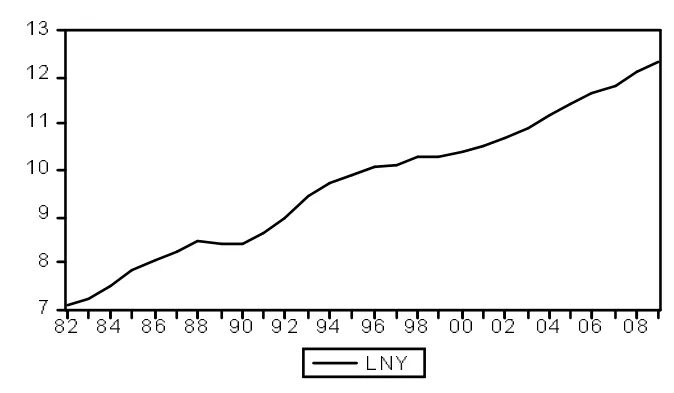
图1 取对数后的固定资产投资总额时间序列趋势图

（2）数据的平稳性检验

对上述数据LnY做一阶差分，生成新的序列LnY1，再对新序列进行时序图分析、自相关图分析或单位根检验，如图2所示。通过时序图可以显著看出，一阶差分后的固定资产投资总额序列趋势性消失，围绕固定值上下波动。进一步地，采用单位根法对数据进行平稳性检验。在5%的显著性水平下，LnY1时间序列数据通过了ADF检验，P值为0.0259，表明一阶差分后的固定资产投资总额时间序列是平稳的，并进行残差白噪声检验，可知该序列为平稳非白噪声序列。由此可以得出取对数后的固定资产投资总额序列是一阶单整的，即I（1）。

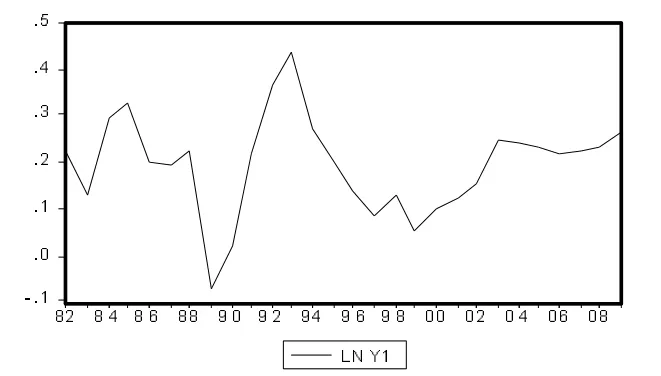
图2 LnY的一阶差分后的时间序列趋势图

3、模型的建立

（1）模型的识别

时间序列ARIMA模型的选择，取决于该序列的自相关系数和偏自相关系数，通过该序列的AC值和PAC值，选择适当阶数的ARMA（p，q）进行拟合。本文利用Eviews软件对上述数据进行时序图的自相关图和偏自相关图分析（图3）。

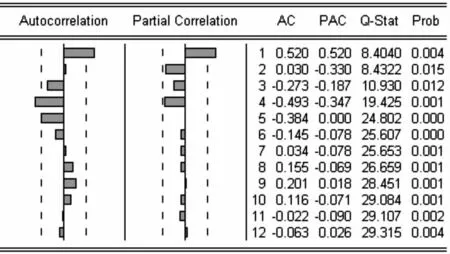
图3 LnY1的自相关图和偏自相关图

（2）模型选择

通过上述的LnY1的自相关图和偏自相关图，可以看出，自相关图的系数K=1和K=4时在二倍标准差之外，其余均在零值附近波动，偏自相关图的系数在K=1之后都落在随机区间内。由此，可以根据ACF和PACF值落入置信区间并呈拖尾现象的特征，考虑建立模型ARMA（1，1）和ARMA（1，4），见表1。

表1 两种模型的最小信息量比较

根据最优模型的最小信息量选择原则，通过上表的比较分析，最小信息量检验显示无论是使用AIC准则还是使用SBC准则，ARMA（1，4）均要优于ARMA（1，1）模型，所以本文选择ARMA（1，4）模型进行拟合。

（3）参数估计与模型检验

运用计量分析方法可对ARIMA（1，1，4）模型进行参数估计与检验，用Eviews软件建立模型并运用最小二乘法对参数进行估计，结果如下：

LnY1=0.194+[AR（1）=0.449，MA（4）=-0.957,BACKCAST=1982]（18.858）（2.482）（-32.174）

R2=0.636，F=21.010，P=0.000，D.W.=1.613

其中，LnY1是对时间序列的原始数据取对数后的一阶差分后的序列，括号里表示参数的t检验值。由上述可知，在5%的显著性水平下，模型各参数均通过了显著性检验，且可决系数为0.636470，模型拟合效果较好。

进一步地，需对模型的残差序列进行白噪声检验。残差的白噪声检验可通过残差自相关图、Q、LB、DW统计量进行判断分析。本文采用Q统计量的值进行判断，检验结果如表2所示。

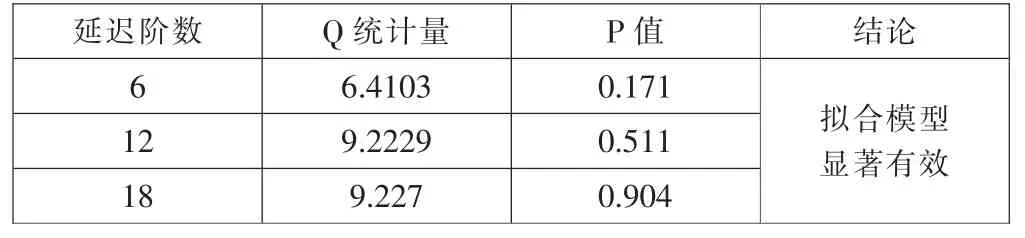
表2 拟合模型残差序列白噪声检验结果

可以看出，在5%的显著性水平下，取对数并一阶差分后的固定资产投资总额拟合模型的残差序列通过白噪声检验，即模型信息提取充分，AR IMA（1，1，4）拟合模型显著有效。

4、模型的预测

图4 LnY1与LnY1F的对比图

预测就是利用序列已观测到的样本值对序列在未来某时刻的取值进行估计。预测包括动态预测和静态预测，对ARIMA模型来讲，一步静态向前预测比动态预测更为准确。

因此，本文采用一步向前静态预测方法，依据上述模型对我国1982—2009年取对数并一阶差分后的全社会固定资产投资总额进行预测，如图4所示。

从图中可以看出,模型的拟合效果较好，预测值围绕着实际值上下波动，误差范围不大，因此预测结果具有一定的参考价值。利用该预测方法，可对2007—2010年我国固定资产投资总额进行预测，结果见表3。

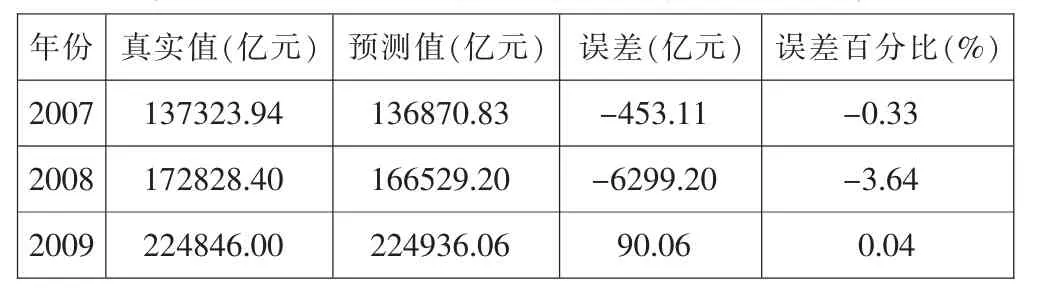
表3 2007—2009年固定资产投资总额预测表

我国固定资产投资总额2007—2009年预测值分别为136870.83亿元、166529.20亿元、224936.06亿元，其相对误差在4%以下，因此，可以认为该模型预测值很好的拟合了固定资产投资总额真实值。

运用该模型，对2010年我国固定资产投资总额进行预测，其预测值为287079.08亿元，在2009年的基础上有所上升，与近几年短期变动趋势一致，与我国宏观经济政策相吻合。

四、结论

固定资产投资总额变化具有明显的非平稳性，因此使用单纯的自回归模型或移动平均模型都无法很好的对投资趋势进行拟合预测，而AR IMA模型可以将两者结合并引入对非平稳序列的差分操作，从而实现对非平稳数列的较好的拟合及预测。

通过以上的分析，我们可以看出运用ARIMA（p，d，q）在对我国固定资产投资总额的分析中，模型较好的拟合了该时间序列数据，模型预测值与真实值之间的误差率很小，随着时间跨度的增加，该模型的预测值与真实值之间的误差率逐渐增大。从短期来看，AR IMA模型在全社会固定资产投资总额的预测上具有一定的可信度，政府可以根据预测结果来制定相应的政策和措施，使全社会固定资产投资达到一个合理的水平，从宏观上调控整个国民经济的整体运作，促进经济的良好健康发展。因此，我们可以用该模型来进行短期的政策指导，特别是在我国出现经济过热或过冷的情况下，合理利用预测数据进行经济运行情况分析，显得尤为重要。

[1] 孙雪：我国进出口总额的动态分析——基于ARIMA模型[J].经济观察，2010（1）.

[2] 魏宁：基于AR IMA模型的陕西省GDP分析与预测[J].安徽农业科学，2010（9）.

[3] 刘培：基于ARIMA模型对上证国债指数的预测研究[J].上海金融学院学报，2009（6）.

[4] 刘勇：AR IMA模型在我国能源消费预测中的应用[J].经济经纬，2007（5）.

[5] 张华初：我国社会消费品零售额ARIMA预测模型[J].统计研究，2006（7）.