基于混沌蚁群算法的物流配送路径问题仿真研究

高大利

（泉州师范学院数学与计算机科学学院，福建泉州362000）

基于混沌蚁群算法的物流配送路径问题仿真研究

高大利

（泉州师范学院数学与计算机科学学院，福建泉州362000）

将混沌与最大最小蚂蚁算法相融合，在蚁群算法的信息素更新规则中加入混沌扰动量避免了在搜索过程中陷入局部极值.测试结果表明混沌蚁群算法能够有效地提高算法的全局寻优能力，对于物流配送路径问题的求解能够获得满意的结果.

物流配送；路径优化；蚁群算法；混沌

1 引言

在物流配送过程中，配送线路安排的合理与否对配送速度、物流成本影响很大；由于配送线路安排涉及多个配送点和复杂的道路网络结构等情况，这就使物流配送路径问题的求解更加困难.随着人工智能技术的不断发展，蚁群算法等新技术被用于解决路径优化及其他一系列组合优化问题；针对蚁群算法求解物流配送路径问题易陷入早熟、停滞、局部最优的缺限.本文将混沌引入蚁群算法，通过仿真实验验证了混沌蚁群算法对于物流配送路径问题的求解是有效的.

2 物流配送路径问题的数学模型

物流配送路径问题是指有L个客户点，已知每个客户点的需求量及位置，至多用K辆车从配送中心到达这批客户点，并且在完成配送任务后，返回物流中心.每辆车载重量一定，要求安排车辆行驶线路使得总成本（如距离、时间等）为最小，且满足以下约束条件：

（1）每条线路上的客户点需求量之和不超过车辆载重量；

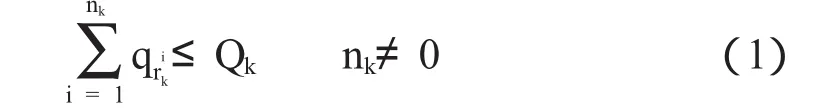
（2）每个客户点的需求必须且只能由一辆车来完成；

（3）配送线路遍历所有客户点.

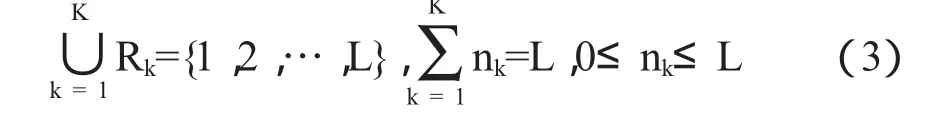
上述符号的含义是：客户点总数L，客户点i的货物需求量qi，从客户点i到客户点j的距离di,j，车辆总数K，车辆k的最大装载量Qk，车辆k配送的客户总数nk，车辆k配送的客户点集合Rk.对于中小规模物流配送路径问题，物流成本和运输路程相关性较强，为简化计算，选择运输路程Z最短为物流配送路径问题的优化目标.

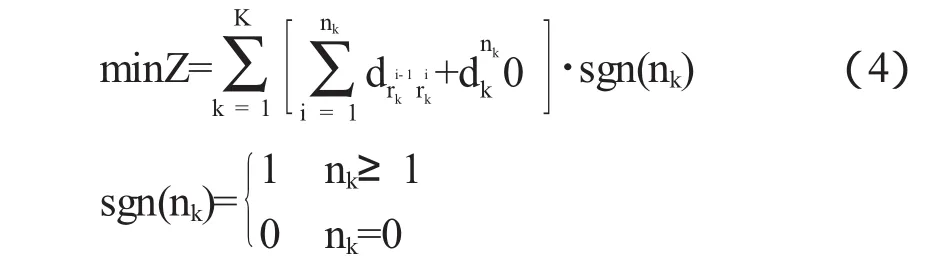
3 物流配送路径问题的混沌蚁群算法

3.1 基本蚁群算法模型

20世纪90年代，Marco Dorigo等人[1]受到自然界中蚁群觅食行为的启发，提出了一种用于求解组合优化问题的新型仿生进化算法——蚁群算法.使用蚁群算法求解物流配送路径问题引入符号定义：t时刻在边(i,j)上的信息素量τij；t时刻在边(i,j)上的启发信息量ηij，可取配送点间距离的倒数，即ηij=1/dij；allowedk表示蚂蚁k下一步允许选择的配送点集合；位于i配送点的蚂蚁k选择j配送点作为下一位置的概率按下式计算：

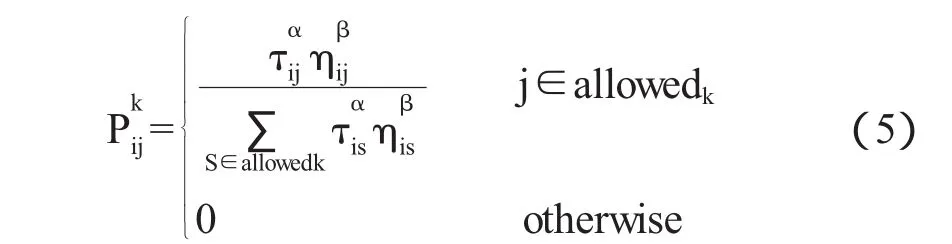
在式（5）中，α，β两个参数分别决定了信息素量和启发信息量的相对影响力；Pkij表示蚂蚁k由配送点i转移到配送点j的概率.当所有蚂蚁都构建好路径后，各边上的信息素将被更新，其规则如下：

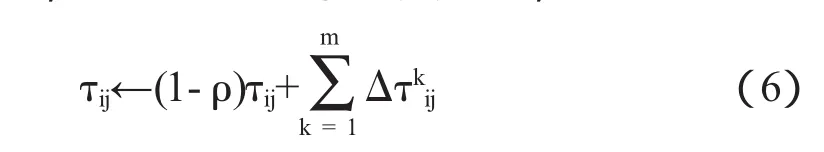
在式（6）中，ρ为信息素挥发系数，其作用是避免信息素的无限积累，0＜ρ＜1；△τkij表示第k只蚂蚁在本次循环中留在边(i,j)的信息素量.Lk表示第k只蚂蚁在本次循环中的所走的路径长度；Q为信息素强度.

上述模型被称为基本蚁群算法模型[2]；参数α，β，ρ，Q等可通过实验方法确定其最优组合，算法停止条件可以设定固定循环次数或者当解不明显时便停止计算.

3.2 混沌与蚁群算法的融合

混沌是自然界广泛存在的一种非线性现象，混沌具有随机性、遍历性、对初始条件的敏感性，能在一定范围内按其自身规律不重复地遍历所有状态，利用混沌的这些性质可以进行优化搜索[3]，并且可以将混沌同其他算法融合，如混沌遗传算法[4]等.

目前对混沌尚无严格的定义，一般地，由确定性方程得到的具有随机性的运动状态称为混沌[5].本文采用Logistic映射作为混沌序列发生器，其迭代公式如下：

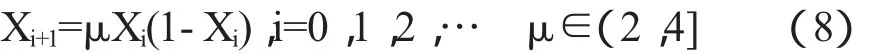
式（8）中，μ为控制参数，μ∈（2，4]；Xi为混沌变量，i=0，1，2，…；尽管式（8）是确定性的，但当μ=4并且X0埸{0，0.25，0.5，0.75，1}时，Logistic映射产生的序列完全呈混沌状态.

为了提高解的多样性和蚁群算法的全局寻优能力，在基本蚁群算法的基础上，采用最大最小蚂蚁系统[6]（MAX-MIN Ant System，MMAS）与混沌融合，具体来说就是在蚁群算法的信息素更新规则中加入混沌扰动量，使解跳出局部极值区间，从而有效地避免搜索过程陷入局部最优.将混沌加入MMAS算法后，各边上的信息素将按式（9）进行更新：

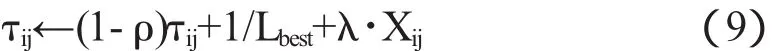
在式（9）中，Xij为混沌变量，可由式（8）迭代得到；λ为调节系数；Lbest为当前迭代的最优路径长度；各条路径上的信息素浓度被限制在[τmin，τmax]之间，超出这个范围的值被强制设为τmin=τmax/5或τmax=1/(ρZ)[7].

3.3 物流配送路径问题的混沌蚁群算法描述

根据混沌蚁群算法模型，使用该算法求解物流配送路径问题的步骤如下：

Step1初始化参数α、β、ρ、λ，X0，最大迭代次数NCmax、迭代计数器NC=0等；

Step2蚂蚁k从配送中心的位置出发；

Step3对蚂蚁k从1到m，重复下面的步骤，直到蚂蚁k走完所有的配送点：

（1）按式（5）选择下一步允许选择的目标配送点；

（2）若配送点j满足式（1）～（3）的约束条件，则将第k只蚂蚁转移到配送点j；

（3）把配送点j加入到已访问过的配送点集合中；

Step4由式（8）生成混沌变量Xij，根据式（9）更新信息素；

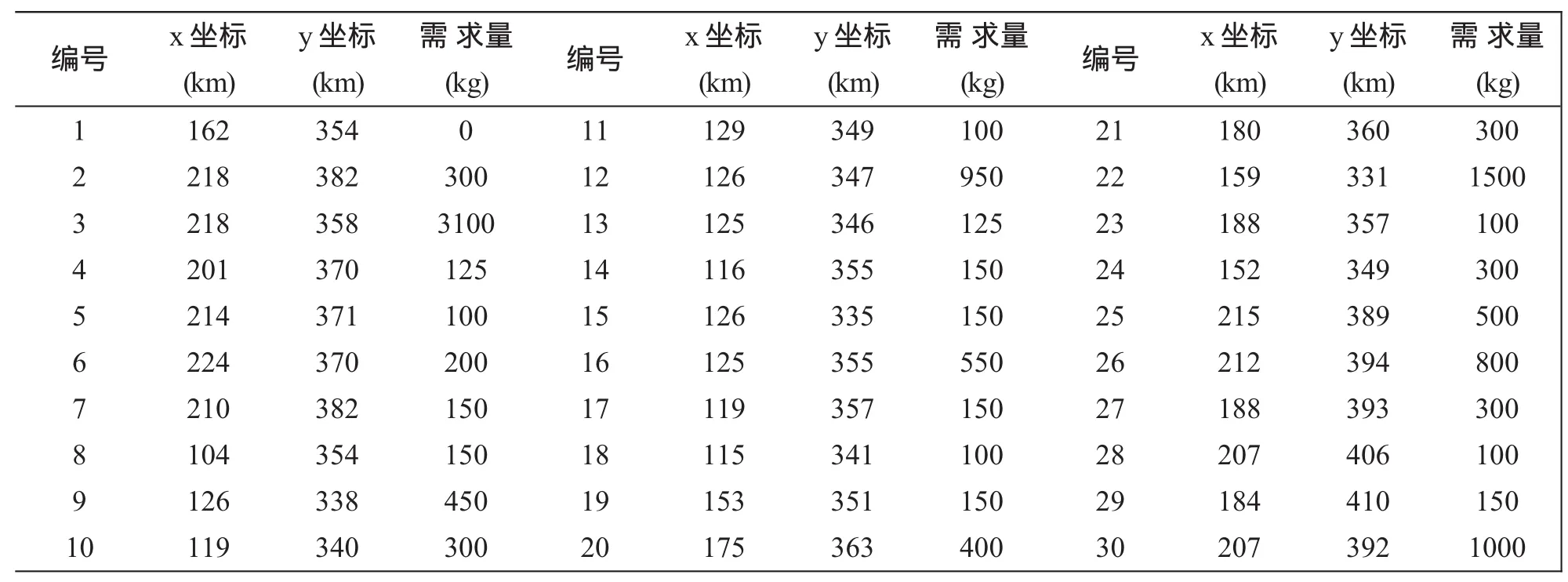
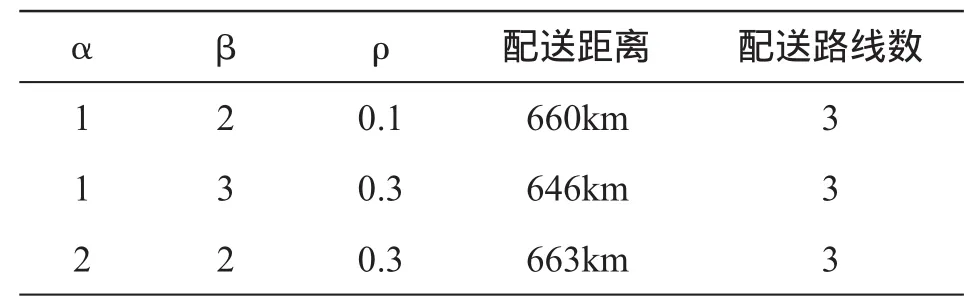
Step5迭代计数器NC=NC+1,如果NC

4 实验及分析

由于蚁群算法中信息启发式因子α、期望值启发式因子β、信息素挥发参数ρ等都是影响物流配送路径问题求解的重要参数，故先通过仿真实验来确定MMAS算法求解物流配送路径问题的最佳参数组合，然后再验证MMAS算法中加入混沌的有效性.实验所用的物流配送路径问题数据来源于VRP测试库，所有实验均在Visual C++6.0环境下进行50次取最优解，算法的最大迭代次数NCmax=1000.在不同参数组合下，采用MMAS算法对VRP测试库中EIL30问题进行求解；已知车辆最大载重量为4500kg，客户数为30个，编号1对应的位置为配送中心，各配送点坐标及需求量如表1.

表1 EIL30问题各配送点坐标及需求量数据表

经过实验，在下列参数组合下，采用MMAS算法求解EIL30问题的较好解如表2所示：

表2 MMAS算法求解EIL30问题的较好解

由表2可知：采用MMAS算法求解EIL30问题的最佳参数组合为：α=1，β=3，ρ=0.3（配送距离为646km，配送路线数为3条）.

为验证MMAS算法中加入混沌的有效性，仍对VRP测试库中的EIL30问题进行求解.参数设置为：α=1，β=3，ρ=0.3；调节系数λ分别取1，10，100；混沌初始值X0分别取随机生成，0.1，0.2，0.3，0.4；经过大量实验，在下列参数组合下，采用混沌蚁群算法求解EIL30问题的较好解如表3所示：

表3 混沌蚁群算法求解EIL30问题的较好解

由表3可知：在以上参数组合下，采用混沌蚁群算法求解的配送距离都小于MMAS算法得出的全局最优解（配送距离为646km，配送路线数为3）；采用混沌蚁群算法求解EIL30问题的最佳参数组合为：α=1，β=3，ρ=0.3，X0=0.1，λ=1（配送距离为622km，配送路线数为3）.

现将MMAS算法、混沌蚁群算法（MMAS算法中加入混沌）这两种算法对EIL30问题求解的具体结果进行对比，如表4所示.

由表4可知：在MMAS算法中加入混沌后，求解的配送距离小于MMAS算法得出的结果，由此说明混沌蚁群算法对物流配送路径问题的求解是有效的.

表4 不同算法求解EIL30问题的实验结果

5 结论

本文利用混沌的随机性遍历性及规律性等特点，将混沌与蚁群算法融合.实验表明：混沌蚁群算法能够有效提高蚁群算法的全局寻优能力，混沌蚁群算法对于物流配送路径问题的求解能够获得满意的结果.此外，本文中MMAS算法及混沌蚁群算法的参数选择，是在大量仿真实验基础上得出的，这些参数组合对于其他组合优化问题的求解具有一定的参考价值.

〔1〕DorigoM,VittorioManiezzo,AlbertoColorni.TheAnt system:optimization by a colony of cooperating agents.IEEE Transactions on systems,Man and Cybernetics,PartB,1996,26(1):29-41.

〔2〕李士勇.蚁群算法及其应用[M].哈尔滨:哈尔滨工业大学出版社,2004.

〔3〕李兵,蒋慰孙.混沌优化方法及其应用[J].控制理论与应用,1997,14(4):613-615.

〔4〕唐巍,郭镇明,唐嘉亨，等.复杂函数优化的混沌遗传算法[J].哈尔滨工程大学学报,2000,21(5):1-5.

〔5〕黄润生,黄浩.混沌及其应用[M].武汉:武汉大学出版社,2005：12.

〔6〕T.Stutzle,H.Hoos.MAX-MIN Ant System.Future Generation Computer Systems,16(8):889-914,2000.

〔7〕马良,朱刚,宁爱兵.蚁群优化算法[M].北京:科学出版社,2008.

TP18

A

1673-260X（2011）01-0025-03