分子在分子筛上扩散行为的分子模拟研究进展
2011-10-22刘立凤高金森
刘立凤,赵 亮,陈 玉,高金森
(中国石油大学(北京)重质油国家重点实验室,北京 102249)
进展与述评
分子在分子筛上扩散行为的分子模拟研究进展
刘立凤,赵 亮,陈 玉,高金森
(中国石油大学(北京)重质油国家重点实验室,北京 102249)
主要综述了采用分子模拟技术考察分子在分子筛上扩散行为的多角度、多层次研究进展,包括分子筛结构、负载量、温度和多组分扩散等因素对扩散系数的影响;在此基础上,进一步介绍了扩散相互作用能和过渡态理论的研究进展,并讨论了分子模拟方法在分子筛扩散研究方面所面临的问题和发展方向。
分子模拟;分子筛;扩散系数;扩散相互作用能;过渡态理论
分子筛因其独特孔道结构而具有优秀的择形及催化功能,被作为催化材料、分离与吸附剂等,广泛应用在石油化工、医药等领域。无论是催化反应还是吸附分离,吸附质分子在分子筛内的扩散过程都是非常重要的,关系到反应速率和分离效率的高低。目前,实验方法对分子筛扩散行为的研究比较广泛,但由于受到实验条件和表征手段的限制,对一些扩散问题很难解释[1]。近年来,随着计算机科学技术与催化技术的发展,分子模拟已成为解决催化领域中实际问题的重要手段。它能够发现实验难以探测到的性质,并可与实验结合解释实验结果,甚至能为实际中无法完成的实验提供新的研究方法,而且方便快捷,能够缩短催化剂研发周期,并降低实验成本[2]。
分子模拟方法[3]主要包含有量子力学法[4]、分子力学方法[5-6]、分子动力学方法[7]和蒙特卡洛[8-10]方法。其中,分子动力学方法多用来计算分子在分子筛孔道内的扩散性质,通过求解体系中分子的运动方程获得分子的运动速度和运动轨迹,再通过统计平均获得扩散的平衡性质和运动特性,并结合蒙特卡罗方法来计算体系的能量变化。国内外很多研究者都通过分子动力学方法研究了吸附质分子在分子筛内的扩散行为,因此,有必要对目前的研究现状进行综述。本文作者对吸附质分子在分子筛内的扩散系数的分类、分子筛结构、负载量和温度对扩散系数的影响、多组分扩散的研究以及从能量角度研究扩散行为的扩散相互作用能和过渡态理论进行了综述。
1 扩散系数的分子模拟
扩散系数是研究传质过程、计算传质速率及化工设计与开发的重要基础数据,在研究分子筛动力学特性过程中,扩散系数可揭示沸石孔道骨架结构与吸附质的相互作用以及吸附质分子在分子筛晶体内微孔中的扩散速率。扩散系数大致可以分为传递扩散系数、互扩散系数和自扩散系数3类[11]:传递扩散系数主要通过宏观的实验方法测得;互扩散系数和自扩散系数都可以通过分子动力学模拟方法计算得到,其中,互扩散系数多用于多组分混合物扩散的研究,而自扩散系数因为其计算简单被广泛地应用在纯组分扩散的研究中。
自扩散系数描述的是在没有浓度梯度的情况下粒子只作布朗运动时的传递性质。由于没有浓度梯度的存在,在最大程度上简化了粒子运动过程所受到的影响。一般来说,采用分子动力学方法计算自扩散系数[12]主要有 Einstein法[13]和 Green Kubo法[14]。Einstein法是计算体系的各种平均平方位移并对其微分得到扩散系数,Green Kubo法是计算体系的各种速度相关函数并对其积分计算得到扩散系数。相比之下Einstein法算法比较简单,故应用较为广泛。Schuring等[15]采用分子动力学方法研究了全硅ZSM-5分子筛内甲烷和乙烷的扩散行为,采用Einstein法计算自扩散系数分别为1.26×10-8m2/s和 5.9×10-9m2/s,和相同条件下的由 PFG NMR方法[16]测得1.05×10-8m2/s、3.8×10-9m2/s在数量级上相符。Nowak等[17]研究了甲烷在全硅沸石中的扩散行为,采用 Einstein法计算计算得到的自扩散系数得数量级为10-9,与PFG NMR实验数据非常吻合。Hussain等[18]采用Einstein法计算了全硅分子筛在300 K,分别负载2个和4个丙烷分子的自扩散系数,分别为4.66×10-9m2/s和3.15×10-9m2/s,计算结果和Caro等[16]PFG NMR测得的扩散系数4.0×10-9m2/s和2.9×10-9m2/s相吻合。由此可见,由分子动力学方法测得的小分子在分子筛内的自扩散系数是比较准确的,和实验测得的数据也相符。
与自扩散系数相比,互扩散系数描述的是所有粒子集体的扩散行为,包含了粒子间的相互作用,所以在相同的条件下互扩散系数要偏大,只有在无限稀释的情况下才相等。互扩散系数是在Fick扩散系数的基础上转化而来的,主要有 Maxwell-Stefan(M-S)和Darken扩散系数。其中,M-S扩散系数研究比较广泛。Krishna等[19]计算了纯组分甲烷、乙烷和丙烷的M-S扩散系数,并研究了M-S扩散系数、自扩散系数和交换系数之间的关系;Krishna等[20]还计算了不同孔道结构分子筛的 M-S扩散系数和交换系数,分析发现交换系数和 M-S扩散系数、负载量通过一常数相关联,而常数的大小表示了分子在分子筛孔道内的限制程度;Jobic等[21]对比了实验方法和分子动力学方法测得的CF4在MFI型分子筛上的M-S扩散系数,结果一致。
由以上可见,常规的分子动力学方法是可以合理计算一些分子的扩散系数,描述一些扩散行为的,但是当吸附质分子在分子筛内的扩散非常慢,扩散系数小于10-12m2/s时,常规的动力学方法就不适用了。进行这种“慢”扩散的分子被长时间地困在邻近吸附位的地方,直到有足够大的动能才能使得分子跨过能垒到达吸附位,而能垒越高所需要的时间越长,可能会长达几个月甚至几年[22-23]。由此可见,常规的分子动力学方法并不适用于较大的吸附质分子。为了解决这种慢扩散的问题,研究者提出了几种方法[24]。比如,温度加速动力学方法(temperature- accelerated dynamics,TAD)[25]在很多假设成立的前提下,可以应用在许多扩散体系。最值得研究的是过渡态理论方法[26-27](transition state theory,TST,在后文中将详细阐述)。Mosell等[28-29]采用 TST方法研究了分子筛微孔内的扩散系数,Smit等[30]采用 TST方法计算了链状烷烃在MFI类型分子筛内的自扩散系数,Beerdsen等[31]提出校正过渡态理论(dynamically corrected transition state theory,dcTST)研究了在非零负载条件下的甲烷等小分子的扩散系数,与TST方法研究无限稀释条件的扩散行为相比有了很大的突破。即便如此,dcTST还是存在不足,对于自由能的计算需要特别的抽样技术以及对于大分子的研究能否实现还需要进一步的证实。
综上所述,采用分子动力学方法计算自扩散系数和M-S扩散系数在一定范围内是准确的,且和实验方法测得的扩散系数相符。然而由于动力学模拟过程中“慢”扩散现象的存在,使得具有较大动力学直径的分子采用分子动力学方法测得的扩散系数不准确,因此需要在过渡态理论的基础上提出更好的方法来解决这个问题。
2 扩散系数影响因素的分子模拟
2.1 分子筛结构对扩散系数的影响
由于分子筛孔道结构复杂,且存在各向异性,使得分子在分子筛的不同孔道、不同方向和不同状态下扩散系数不同。例如,张国等[32]研究了1-丁烯和正丁烷在 MCM-22分子筛两个独立孔道中的扩散系数。结果表明,1-丁烯和正丁烷在十元环孔道中的扩散系数明显低于在超笼中的扩散系数,吸附质分子在超笼的底部和顶部的扩散系数明显低于在超笼中心的扩散系数。陈玉平等[33]采用分子动力学方法研究乙烷、丙烷在MOR分子筛上的扩散系数,结果表明各个方向上的扩散系数不同,Z方向上的扩散系数最大。由上可见,由于分子筛晶内孔道结构不同,对分子扩散过程中的相互作用力不同,致使分子的扩散率和扩散位移不同,扩散系数也存在差异。
采用分子动力学方法研究分子筛模拟晶胞会呈现两种状态,即柔性的和刚性的状态。刚性状态下的晶胞分子筛的原子不动,节约了大量的运算时间,这是人们所期待的,但是柔性状态下的晶胞原子会不会影响分子的扩散行为进而影响扩散系数呢?许多研究者对这两种状态进行了对比。Kopelevich等[34]研究发现惰性气体分子在柔性状态下的扩散系数要比刚性状态下的扩散系数大很多,而 Demontis等[35-36]研究发现分子筛刚性和柔性状态对甲烷扩散系数的计算影响较小。曾勇平等[37]计算了乙硫醇分子MOR沸石中晶格原子刚性和柔性两种状态下的扩散系数,发现柔性状态下的扩散系数比刚性状态下的扩散系数要小。Leroy[38]和Zimmermann[39]等又研究发现,对于同一模拟体系,由于分子筛作用参数不同,柔性状态与刚性状态相比,扩散系数也可能增大也可能减小。从以上的讨论中看出,晶胞的刚性和柔性状态对于扩散系数的影响是非常复杂的,但都没有给出确切的结果。Demontis等[40]还认为以时间为函数计算扩散系数或大的客体分子在分子筛内扩散时分子筛骨架呈刚性状态时是不合理的,希望能通过更高级的动力学模拟软件和并行计算机出现来解决目前存在的问题。
2.2 负载量对扩散系数的影响
负载量是分子筛扩散性质重要的影响因素,一般说来, 随着负载量的增加,吸附质分子之间的作用力增强,扩散行为会受到限制,扩散系数会降低。Rungsirisakun等[41]应用分子动力学方法研究了在FUA分子筛中分别放置2、4、6、8个苯分子的自扩散系数,发现苯的扩散系数则随着分子个数的增加而下降。曾勇平等[37]采用分子动力学方法模拟比较了不同负载量的乙硫醇分子在 ZSM-5和 MOR两种拓扑结构沸石中的扩散系数,模拟结果表明,对于这两种沸石,负载量增加,扩散系数都减小。然而也有研究表明,随着负载量的增加扩散系数是增加的。Krishna等[42]采用分子动力学方法研究了7种分子(He,Ne,Ar,Kr,H2,N2,CO2)在全硅分子筛上的扩散系数,发现在一定范围内随着负载量的增加,扩散系数是先降低后增加到最大值再逐渐降低的。以上研究由于考察范围和体系的差异出现了不同的结果,也没有合理的解释。而Dubbeldama等[43]同样研究发现,甲烷和乙烷在LTA型分子筛上的扩散系数也是先降低后增加到最大值再逐渐降低的,并结合自由能的变化对这种现象作出了解释:随着负载量的增加分子与分子间的作用力不断增强,限制了分子的扩散,扩散系数也随之降低;后负载量不断增加,分子之间的排斥力克服了分子与分子筛的吸引力,使得自由能垒降低了,扩散系数出现了最大值;又随着负载量的不断增加,分子之间的作用力占了主导地位,扩散系数又不断降低。Nanok等[44]研究甲醛在NaX分子筛上扩散随负载量变化时也出现相同的规律,并用集体效应(collective effects)和位阻效应(steric hindrance)解释了出现这一规律的原因。
2.3 多组分分子扩散系数的研究
仅仅研究纯组分在分子筛内扩散是不能全面考察分子筛的扩散性质的,二元甚至多元混合组分扩散行为的研究更接近实际情况,对混合物的分离和化学反应都有非常重要的意义。为了正确理解混合物的扩散行为,很多研究者采用分子动力学方法结合蒙特卡罗方法进行了研究,发现混合物中的有些分子扩散变慢了,而有些分子的扩散变快了,Krishna等[45-47]认为这是扩散物种间的耦合效应,是由参与扩散的混合物分子之间相互作用产生。例如,Yue等[48]采用分子动力学方法研究了 CO2/Benzene的混合物在全硅MFI型分子筛上的扩散行为,发现混合物中的CO2的扩散系数比纯组分时高了一个数量级,且随着CO2负载量的增加,扩散系数增加了。Krishna等[49]还发现CO2/CH4混合物在DDR型分子筛上扩散时,CO2分子强烈的吸附在交叉孔道处阻碍了CH4进入笼内扩散,使得CH4的扩散系数降低了。对于混合物的扩散行为,在某些观点上有研究者还存在分歧。Hussain等[18]研究了甲烷、乙烷和丙烷混合物在全硅FMI型分子筛上的扩散行为,认为乙烷和丙烷的混合物扩散时乙烷的扩散系数比丙烷要低;3种分子混合扩散时扩散系数几乎相等。而 Krishna等[50]研究了相同的体系,发现和纯组分扩散时相比,乙烷的扩散系数降低了,丙烷的增加了,但乙烷和丙烷相比扩散系数要大;而对于三组分扩散与纯组分相比,甲烷扩散系数增加了,丙烷下降了,而乙烷未发生太大的变化,但它们扩散系数的大小顺序为甲烷>乙烷>丙烷。由此可见,多组分扩散的研究是比较复杂的但又非常的重要,很具有挑战性,需要研究者采用多种方法进行更深入的研究。
2.4 温度对扩散系数的影响
不论是采用实验方法还是分子模拟方法,温度对于扩散系数的计算都是非常重要的影响因素。随着温度的升高,分子的热运动加剧,动能增加,扩散能力增强,扩散系数也随之增加。这种变化趋势符合Arrhenius行为,而这种行为可以在很多体系中观察到。Ahunbay等[51]采用分子动力学方法研究了MTBE在不同温度下silicalite-1中的扩散系数,负载量一定的情况下随着温度的升高扩散系数增加。Plant等[52]研究了甲烷在NaY分子筛不同温度下的扩散系数,结果得到随着温度的增加扩散系数不断增加。Krishna等[53]研究了苯在 NaX和 silicalite-1分子筛的M-S扩散系数的变化规律,符合Arrhenius行为(见图1),同时他们也研究发现在低温下会发生Non-Arrhenius行为(见图2)。López等[54]研究甲烷在 MFI型分子筛温度对扩散系数的影响时也观察到了 Non-Arrhenius行为,并结合能量及自由能曲线作出了解释,出现这种现象是由于在低温和高温时分子所克服能垒不同,在低温时分子扩散的主要能垒是分子离开分子筛孔道内的最优吸附位上的能垒,而在高温时分子需要克服离开交叉孔时的能垒。

图1 多种分子在不同分子筛上不同温度下的M-S扩散系数

图2 异丁烯在MFI分子筛上扩散系数的Non-Arrhenius行为
综上所述,虽然采用分子动力学方法计算扩散系数是在一定程度上解释了一些扩散行为,但仍有一些问题没有得到很好的解决,比如“慢”扩散、多组分扩散的问题等。因此,采用分子模拟方法研究扩散系数仍然是一个很大的挑战,需要进行更多更深入的研究。
3 扩散相互作用能的分子模拟
分子模拟方法作为一种实验的辅助手段[55],不仅可以计算宏观性质扩散系数,还可以考察实验手段难以深入研究的物理和化学过程,从能量的角度研究物质的结构与性能关系。许多学者通过分子模拟技术研究分子与分子筛之间的相互作用能和扩散能垒,来探讨反应物与产物在分子筛孔道中的扩散特性,考察分子筛对反应物与产物分子的择形性能。
扩散是不可逆的宏观过程,但其中也包含了一些可逆的微观步骤,分子从一个吸附位跳跃到另一个吸附位,然后也可能继续向前跳跃,也可能跳回原来的吸附位。分子这种跳跃的过程和历史无关的现象被描述为随机行走理论[56]。随机行走理论是分子在晶格内跳跃时由于受到随机力的影响向各个可能的孔道方向跳跃的数学模型,而采用动力学方法研究随机行走模型并没有给出太多给定体系的扩散特性的信息。因此,研究分子在给定分子筛笼内或孔道内扩散作用能变化时,一般采用固定扩散路径的方法。固定路径扩散是指进行扩散模拟时,分子在分子筛孔道中沿着预先定义的路径,按照设定的步长从起点移动到终点,在每个位置上进行优化寻找能量局部最低构象,并计算各点的非键相互作用能,绘制扩散相互作用能曲线。
非键相互作用能是指分子在分子筛孔道内沿某一路径扩散时[57],受到孔道周围原子的影响而产生热力学作用。各点的相互作用能采用式(1)计算。

式中,E1为各点的相互作用能;EZM、EZ和EM分别为分子筛骨架原子与分子键的相互作用能、分子筛骨架原子间的相互作用能和芳烃分子间的相互作用能。在相互作用能曲线上,会出现能量最低位点(favorable site)和能量最高位点(unfavorable site),相邻两个能量位点的差即为扩散能垒。许多研究者通过对扩散相互作用能和扩散能垒的分析,研究了多种分子筛的择形性能、分子扩散与分子直径和分子筛孔道结构的关系以及分子在不同孔结构的分子筛内的扩散特性。
侯廷军等[58]研究了苯分子在纯硅 MCM-22型分子筛十元环窗口附近经过十二元环超笼扩散到另一个十元环窗口中的扩散行为。图3 是苯分子在扩散过程中从一个孔道交叉处质心离平面的距离和非键相互作用能之间的关系。从图3上可以清楚地看到,苯分子在运动过程中十元环A点和C点体系的能量又远高于十二元环B点体系的能量,也就是说,苯分子在十二元环超笼内可以较为自由迁移,而通过十元环窗口从一个超笼扩散到附近的超笼时则需要较高的激发能量,这个能量大约为100 kJ/mol。以上研究结果表明,苯分子的扩散和吸附主要在十二元环超笼内发生。朱丽荔等[59]又研究了比苯分子较大的间二甲苯和邻二甲苯在 MCM-22分子筛的十二元环扩散到另一个十二元环时的相互作用能,并解释了间二甲苯和邻二甲苯吸附量存在差别的原因(见图4),可以发现间二甲苯和邻二甲苯在经过十元环窗口附近时会有一个非常明显的势垒,间二甲苯大约为230 kJ/mol,邻二甲苯大约为520 kJ/mol,而在十二元环中心部位扩散时相互作用能比较平缓。也就是说,邻二甲苯和间二甲苯在扩散进入分子筛内部穿过十元环时会存在较大的势垒,而邻二甲苯的势垒要大于间二甲苯的势垒,所以间二甲苯可以克服这个势垒到达分子筛的内部,但邻二甲苯不能克服这个势垒而只能在分子筛的表面发生吸附和扩散,使得间二甲苯和邻二甲苯吸附量存在很大的差别。
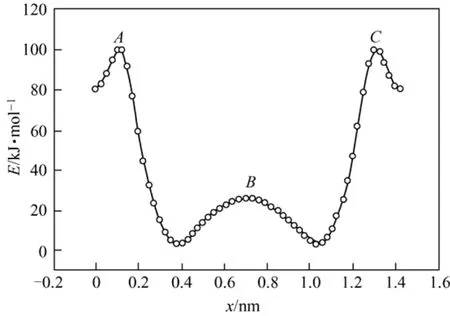
图3 苯分子质心离平面的距离和非键相互作用能之间的关系
Bharathi等[60]采用能量最小化和分子动力学方法考察了LTL、MAZ、MOR、ZSM-5这4种不同孔结构的分子筛对4-氨基苯酚和4种可能的酰化产物的择形功能。通过分析各个分子在各种分子筛的相互作用能曲线和计算扩散能垒得到,分子筛LTL、MAZ、MOR对于5种分子的扩散几乎没有选择性,而 ZSM-5分子筛对于产物乙酰苯胺表现出很好的选择性。Tomlinson-Tschaufeser等[61]用分子动力学和能量最小化方法对丁烯异构体在 55种不同孔结构分子筛的择形性进行了考察并排序,其中 TON结构的分子筛具有最高的选择性,其次是 RHO和MFL,而 TON分子筛可以有效地以不同的方式汇集不同的丁烯异构体。Deka等[62-63]不仅对分子筛的择形性进行了考察,还更深入地探讨了分子在分子筛内的扩散机制。他们研究乙苯、异丁苯以及其烷基转化和歧化反应产物邻、间、对-异丁基乙基苯分子在分子筛OFF、MTW、CAN和MEI上的扩散能垒,发现产物对-异丁基乙基苯选择性的优劣顺序为MEI < OFF≈MTW < CAN,并分析得到通道型孔的分子筛(例如MEI)比笼型孔的分子筛(例如CAN)具有更好的择形性,分子筛孔道和扩散分子直径相近的分子筛有更高的择形功能;并提出反应物与产物在分子筛晶格内的扩散特征依赖于扩散分子的直径和分子筛的孔结构,扩散分子更倾向吸附于分子筛表面作用能大的位置,也就是说分子与分子筛表面的作用力控制了分子在分子筛内的扩散机制。

图4 间二甲苯和邻二甲苯在十二元环之间迁移的相互作用能曲线
除了通过扩散能垒对分子筛的择形性进行了分析,还有很多研究者对扩散能垒与分子孔径,分子筛结构和孔道大小之间的关系进行了研究。Waghmode等[64]研究了甲醇、苯、甲苯、二甲苯(邻二甲苯、对二甲苯和间二甲苯)等分子的最大直径与在MCM-22分子筛中的扩散能垒得关系,发现分子直径甲醇<苯<甲苯<二甲苯,而各个分子的扩散能垒的关系是甲醇<苯<甲苯<二甲苯,由此得出在分子的扩散能垒和分子的直径有关;同时又发现即使二甲苯分子的同分异构体的分子直径关系是邻二甲苯<对二甲苯<间二甲苯,但他们扩散能垒的关系是邻二甲苯>对二甲苯>间二甲苯,由此得出扩散能垒除了和分子的直径有关外还和分子的构型有关。代振宇等[65]用分子动力学方法计算了 FCC汽油模型化合物分子(正庚烷、正庚烯、2-甲基己烷、2-甲基己烯、甲基环己烷和甲苯)在Y、ZSM-5和β分子筛孔道中的扩散能垒。Y和β分子筛孔径较大,模型化合物分子在这两种分子筛中的扩散能垒差别不大;ZSM-5 分子筛的孔径较小,与汽油模型化合物分子尺寸相近,不同结构模型化合物分子在ZSM-5 分子筛中的扩散能垒具有明显的差别,致使造成对产物的选择性不同。杨超等[57]研究了在同一分子筛不同孔道中的扩散能垒,计算了甲苯歧化反应中的反应物甲苯、产物苯和二甲苯同分异构体在ZSM-5分子筛的直孔道和正弦孔道内的扩散能垒,发现芳烃分子在正弦孔道中的扩散能垒均高于直孔中的扩散能垒,且在达直孔道与弯孔道交叉处时能量最小。因此推断得出,由于ZSM-5分子筛正弦孔道尺寸小于直孔的孔尺寸,当芳烃分子进入ZSM-5分子筛后它们更倾向于在 ZSM-5分子筛的直孔中扩散。综上所述,吸附质分子在分子筛内的扩散能垒与分子的大小和构型、分子筛孔径的大小和结构有关。
本节通过对固定扩散路径相互作用能和扩散能垒的研究,解释了工业生产中的一些实际问题,比如,间二甲苯和邻二甲苯吸附量存在差别的原因、多种分子筛择形性的优劣顺序、ZSM-5分子筛对FCC汽油组分优良的选择性可实现增产低碳烯烃的目的等。可见,采用分子模拟方法考察分子筛扩散作用能的变化在扩散相关性质的研究是高效实用的,可推广到多种分子筛体系的考察中。
4 过渡态理论的分子模拟
过渡态理论(TST)最初是用来研究分子在分子筛“慢”扩散问题(slow diffusion)的,假设分子的扩散行为可以看做分子从晶格的A位置到B位置的跳跃过程(A、B指代任意位置),A位置和B位置之间要有足够大的能垒使得跳跃过程成为一个稀有事件(rare event),且随后的跳跃过程和前面是无关的。由作为反应坐标函数的自由能计算得到跳跃频率,便可得到扩散系数。过渡态理论在传统方法上有了发展,由原来应用在一维有序参数扩展到多维有序参数;校正过渡态过渡态理论确保了分子从A位置经过最大能垒到达B位置的过渡状态,使测得的扩散系数更加精确。
采用过渡态理论研究扩散行为的一个优势是不仅可以计算扩散系数,还可以得到以反应坐标为函数的自由能曲线。自由能曲线的计算有Monte-Carlo方法模拟的 Widom Sampling和Monte-Carlo方法或动力学方法模拟的 Histogram Sampling两种方法。很多研究者不但采用过渡态理论计算得到了“慢”扩散状态下的扩散系数,还结合自由能变化研究了一些特殊的扩散现象。例如,在第2.3节和第2.5节中提到的Dubbeldama等[43]结合自由能的变化解释了甲烷和乙烷在 LTA型分子筛上的扩散系数先降低后增加到最大值再逐渐降低的的现象;López等[54]结合能量及自由能曲线解释了甲烷在 MFI型分子筛上扩散系数随温度变化的Non-Arrhenius行为。
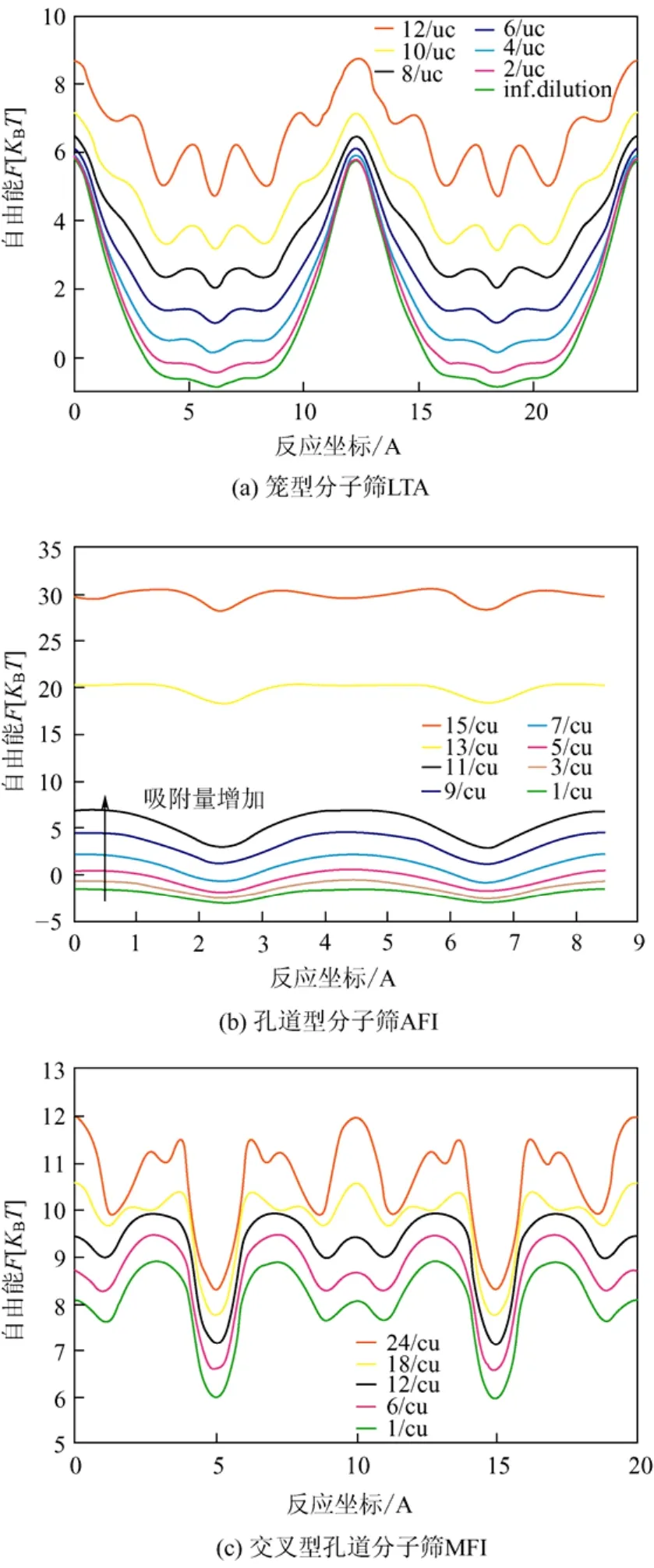
图5 各种分子筛在300 K的温度下以负载量为函数的自由能F

图6 各种分子筛以负载量为函数的自扩散系数DS和互扩散系数DC
Beerdsen等[11]通过采用过渡态理论方法分析甲烷在多种分子筛内不同负载量下的自由能曲线,并根据分子筛的孔道结构和扩散特性将分子筛分为 3类:笼型(cage-type)分子筛(SAS、CHA、ERI和LTA)、孔道型(channel-type)分子筛(MTW、LTL和AFI)、交叉型孔道(intersecting channel-type)分子筛(ISV、BOG和MFI)。如图5和图6中所示,笼型分子筛的笼由狭窄的窗口连接,当甲烷分子在分子筛内扩散时会出现较大的能垒,随着扩散分子的逐渐增多,分子之间的作用力增强,分子筛笼内的自由能增加;当甲烷分子多到分子筛内几乎填满时,窗口附近的自由能垒降低了,这使得扩散系数增加;当甲烷的密度达到过高时由于堆积和自由体积的影响,扩散性能进一步降低,扩散系数也进一步降低。对于孔道型分子筛,随着甲烷分子数的增加,笼内的自由能增加了,但是比阻碍处的能垒还要高,这使得扩散系数随着负载量的增加不断降低。还发现分子筛的孔道越光滑,扩散系数降低越快。交叉型孔道分子筛由于孔道直径和长度不同,交叉处又存在势阱,使得甲烷在分子筛内的扩散变得非常复杂,基本能量变化趋势和孔道型分子筛相似,扩散系数随着负载量的增加不断降低,但由于孔道结构的差异自由能又会出现不同的变化。由以上分析得出,负载量的变化对分子筛扩散的影响是和分子筛的扑拓结构密切相关的。
虽然通过过渡态理论可以计算一些体系的自由能曲线和扩散系数,但就目前为止,所研究的客体分子大都为甲烷小分子,其它分子以及多负载量的研究并不多见。然而通过计算自由能来研究慢扩散的方法有很多种[66],比如Metadynamics方法[67],一些研究[68-69]报道了使用该法来分析小分子配体(CO 等)在一些蛋白质孔道内的扩散路径。过渡态理论的研究虽有了一些成绩但仍是研究的难点[70],在将相同的方法应用到其它吸附质分子和体系的同时,要不断加强理论的研究,完善过渡态理论。
5 结 语
高版本计算软件的开发、高性能计算机服务器的建立,促进了分子模拟方法在分子筛内扩散行为的研究,提高了传统实验的效率,并取得了一定进展。总的来说,多数研究是通过分子模拟方法计算分子在分子筛内的扩散系数,均方位移以及扩散作用能来阐述扩散行为的。基于以上研究,对今后的发展提出3点期望。
(1)基于过渡态理论已经提出了很多方法[70]来解决传统动力学模拟时间长的问题,但“慢”扩散的研究仍然是研究的难点。例如,过渡态理论大多数研究的是简单小分子体系,而能否用此方法解决大吸附质分子在分子筛内扩散受限的问题仍需进一步的研究。过渡态理论多集中于自扩散系数的计算,互扩散系数的研究也是非常重要的。
(2)反应物与产物的扩散行为对于催化反应以及产物的选择性都非常重要,如果采用分子模拟方法将反应和扩散过程结合起来会具有更重要的研究价值。
(3)分子模拟方法研究的多是分子筛的理想结构,而对于含有其它金属离子的分子筛以及发生孔结构变化后分子筛的扩散行为模拟较少。如果能掌握这些多元化分子筛的扩散行为规律将为新型多孔材料的设计提供重要的理论基础。
[1]Snatos J M,Fomriga A B,Figueroa-Villar J. NMR and molecular modeling study of ligand exchange induced structural changes in diruthenium complexes[J].J. Mol. Surtet.,2002,608(2-3):143-149.
[2]陈汇勇,奚红霞,李忠,等. 分子筛构-效关系的分子模拟研究进展[J]. 化工进展,2007 ,26(7):914-920.
[3]杨小震. 分子模拟与高分子材料[M]. 北京:科学出版社,2002.
[4]Leszezynski J,Computational Chemistry :Reviews of Current Trends(Volume 6)[M]. Singapore:World Scientific Publishing Co. Pte. Ltd.,2001.
[5]汪文川等译. 分子模拟——从算法到应用[M]. 北京:化学工业出版社,2002.
[6]钟璟,黄维秋,殷开梁. 分子模拟技术在气体膜分离研究中的应用[J]. 化工进展,2005,24(7):743-748.
[7]Alder B J,Wainwright T E. Phase transition for hard-sphere system[J].J. Chem. Phys.,1957,27:1208-1209.
[8]Hammersley J M,Handscomb D C. Monte Carlo Method[M]. London:Methuen,1964.
[9]Tocher K. The Art of Simulation[M]. London:The English Univ. Press,1963.
[10]裴鹿成,张孝泽. 蒙特卡罗方法及其在粒子输运问题中应用[M].北京:科学出版社,1980.
[11]Beerdsen E,Dubbeldam D,Smit B. Understanding diffusion in nanoporous materials[J].Phys. Rev. Lett.,2006,96(4):044501-044504
[12]邓平晔,张冬海,田亚峻,等. 自组装的分子动力学模拟[J]. 化学进展,2007,19(9):1249-1257.
[13]Allen M P,Tildesley D J. Computer Simulation of Liquids[M]. Oxford:Clarendon Press,1987.
[14]Hansen J P,McDonald I R. Theory of simple Liquids[M]. 2nd edition. London:Academic Press,1986.
[15]Schuring D,Jansen A P J,Santen R A van. Concentration and chain length dependence of the diffusivity of alkanes in zeolites studied with MD simulations[J].J. Phys. Chem. B,2000,104:941-948.
[16]Caro J,Bulow M,Schirmer W,et al. Microdynamics of methane,ethane and propane In ZSM-5 type zeolites[J].J. Chem. Soc.,1985,81:2541-2550.
[17]Nowak A K,den Ouden C J J,Pickett S D,et al. The mobility of absorbed species in zeolites:Methane,ethane and propane diffuse ities[J].Journal of Physical Chemistry,1991,95(2):848-854.
[18]Hussain I,Titiloye J. Molecular dynamics simulations of the adsorption and diffusion behaviour of pure and mixed alkanes in silicalite[J].Micropor. Mesopor. Mater.,2005,85:143-156.
[19]Krishna R,vanBaten J M. An investigation of the characteristics of Maxwell-Stefan diffusivities of binary mixtures in silica nanopores [J].Chemical Engineering Science,2009,64:870-882.
[20]Krishna R,vanBaten J M. Unified Maxwell-Stefan description of binary mixture diffusion in micro- and meso- porous materials[J].Chemical Engineering Science,2009,64:3159-3178.
[21]Jobic H,Skoulidas A I,Sholl D S. Determination of concentration dependent transport diffusivity of CF4in silicalite by neutron scattering experiments and molecular dynamics[J].J. Phys. Chem. B,2004,108:10613-10616.
[22]Smit B. Molecular simulations of zeolites:Adsorption,diffusion,and shape selectivity[J].Chem. Rev.,2008,108:4125-4184.
[23]Nagumo R,Takaba H,Nakao S. Accelerated computation of extremely ‘slow’ molecular diffusivity in nanopores[J].Chemical Physics Letters,2008,458:281-284.
[24]Voter A F,Montaleni F,Germann T C. Extending the time scale in atomistic simulation of materials[J].Annu. Rev. Mater. Res.,2002,32:321-346.
[25]Sorensen M R,Voter A F. Temperature-accelarated dynamics for simulations of infrequent events[J].J. Chem. Phys.,2000,112:9599-9606.
[26]Truhlar D G,Hase W L,Hynes J T. Current status of transition-state theory[J].J. Phys. Chem.,1983,87:2664-2682.
[27]Garcia-Viloca M,Gao J,Karplus M,et al. How enzymes works:Analysis by modern rate theory and computer simulations[J].Science,2004,303:186-195.
[28]Mosell T,Schrimpf G,Hahn C,et al. Cage-to-cage jumps of xenon in zeolite NaY:Transmission coefficients from molecular dynamics simulations[J].J. Phys. Chem.,1996,100:4571-4581.
[29]Mosell T,Schrimpf G,Brickmann J. Xenon diffusion in zeolite NaY:Transition-state theory with dynamical corrections[J].J. Phys.Chem.,1996,100:4582-4590.
[30]Smit B,Loyens L D J C,Verbist G L M M. Simulation of adsorption and diffusion of hydrocarbons in zeolites[J].Faraday Discuss,1997,106:93-104.
[31]Beerdsen E,Smit B,Dubbeldam D. Molecular simulation of loading dependent slow diffusion in confined systems [J].Phys. Rev. Lett.,2004,93:248301.
[32]张国,郑清川,周欣,等. 分子动力学模拟 1-丁烯和正丁烷在MCM-22分子筛中的扩散行为[J]. 高等化学学报,2009,30:1611-1614.
[33]陈玉平,吕玲红,邵庆,等. 烷烃在丝光沸石型分子筛中的吸附和扩散行为[J]. 物理化学学报,2007,23(6):905-910.
[34]Kopelevich D I,Chang H C. Does lattice vibration drive diffusion in zeolites? [J].J. Chem. Phys.,2001,114:3776-3789.
[35]Demontis P,Fois E,Suffritti G,et al. Molecular dynamics studies on zeolites. 4. Diffusion of methane in silicalite[J].J. Phys. Chem.,1990,94:4329-4334.
[36]Demontis P,Suffritti G,Mura P. A molecular dynamics study of diffusion of methane in silicalite molecular sieve at high dilution[J].Chem. Phys. Lett.,1992,191:553-560.
[37]曾勇平,居沈贵,陈长林. 乙硫醇在MFI和MOR沸石中扩散行为的分子动力学模拟[J]. 燃料化学学报,2007,359(4):470-476.
[38]Leroy F,Rousseau B,Fuchs A H. Phys. Self-diffusion ofn-alkanes in silicalite using molecular dynamics simulation:a comparison between rigid and flexible frameworks[J].Chem. Chem. Phys.,2004,6:775-783.
[39]Zimmermann N E R,Jakobtorweihen S,Beerdsen E,et al. In-depth study of the influence of host-framework flexibility on the diffusion of small gas molecules in one-dimensional zeolitic pore systems[J].J. Phys. Chem. C,2007,111:17370-17381.
[40]Demontis P,Giuseppe B. A comment on the flexibility of framework in molecular dynamics simulations of zeolites[J].Microporous and Mesoporous Materials.,2009,125:160-168.
[41]Rungsirisakun R,Nanok T,Probst Mi,et al. Adsorption and diffusion of benzene in the nanoporous catalysts FAU,ZSM-5 and MCM-22:A molecular dynamics study[J].Graphics Modell.,2006,24:373-382.
[42]Krishna R,van Baten J M. Insights into diffusion of gases in zeolites gained from molecular dynamics simulations[J].Microporous Mesoporous Mater.,2008,109:91-108.
[43]Dubbeldama D,Beerdsen E,Vlugt T J H,et al. Molecular simulation of loading-dependent diffusion in nanoporous Materials using extended dynamically corrected transition state theory[J].The Journal of Chemical Physics,2005,122:224712.
[44]Nanok T,Vasenkov S,Keil F J,et al. Molecular dynamics simulation study of the concentration dependence of the self-diffusivity of methanol in NaX V zeolite[J].Microporous and Mesoporous Materials,2010,127 :176-181.
[45]Krishna R. Chem. Predicting transport diffusivities of binary mixtures in zeolites[J].Phys. Lett.,2002,355:483-489.
[46]Krishna R,Baur R. Analytic solution of the Maxwell-stefan equations for multi component permeation across a zeolite membrane[J].Chem. Eng. J.,2004,97:37-45.
[47]Krishna R,Paschek D,Self-diffusivities in multicomponent mixtures in zeolites[J].Phys. Chem. Chem. Phys.,2002,4:1891-1898.
[48]Yue X P,Yang X N,Molecular simulation study of adsorption and diffusion on silicalite for a benzene/CO2mixture[J].Langmuir,2006,22(7):3138-3147.
[49]Krishna R,van Baten J M. Influence of segregated adsorption on mixture diffusion in DDR zeolite[J].Chemical Physics Letters,2007,446:344-349.
[50]Krishna R,van Baten J M,Diffusion of alkane mixtures in zeolites:Validating the Maxwell-stefan formulation using MD simulations[J].Phys. Chem. B,2005,109:6386-6396.
[51]Ahunbay M G ktug,Karvan O,Erdem-Senatalar A. MTBE adsorption and diffusion in silicalite-1[J].Micropor. Mesopor. Mater.,2008,115:93-97.
[52]Plant D F,Maurin G,Bell R G. Diffusion of methanol in zeolite NaY:A molecular dynamics study[J].J. Phys. Chem. B,2007,111(11):2836-2844.
[53]Krishna R,Baur R Sep. Modelling issues in zeolite based separation processes[J].Purif. Technol.,2003,33:213-254.
[54]López F,Perez R,Ruette F,et al. Interplay of entropic and memory effects in diffusion of methane in silicalite zeolites[J].Phys. Rev. E,2005,72:61111.
[55]刘丹,张晓彤,桂建舟,等. 分子模拟在分子筛催化研究中的应用[J]. 石油化工高等学校学报,2004,17(3):9-12.
[56]Beerdsen E. On diffusion in zeolites a simulation study[D]. Doctoral Dissertation of the Institutional Repository of the University of Amsterdam,2007.
[57]杨超,赵天波,周涵. 甲苯歧化反应物与产物在ZSM系分子筛孔道中扩散特性的分子模拟[J]. 石油学报,2006,22:14-19.
[58]侯廷军,朱丽荔,徐筱杰. MCM-22型分子筛中苯分子吸附行为的蒙特卡罗模拟研究[J]. 化学学报,2000,58:1216-1220.
[59]朱丽荔,侯廷军,徐筱杰. ITQ-1分子筛中二甲苯吸附特征的计算机模拟[J]. 物理化学学报,2000,16:981-985.
[60]Bharathi P,Deka R C,Sivasanker S,et al. Diffusional characteristics of substituted anilines in various zeolites as predicted by molecular modeling methods[J].Catalysis Letters,1998,55(2):113-120.
[61]Tomlinson-Tschaufeser P,Freeman C M. Computer simulation studies of the selectivity of zeolitesfor different butane isomers[J].Catalysis Letters,1999,60(1-2):77-81.
[62]Deka R C,Vet rival R,Miyamoto A. Computational studies on the diffusion behaviour of alkylaromatics in large pore zeolites[J].Topics in Catalysis,1999,9(3-4):225-234.
[63]Deka R C,Vet rival R. Adsorption sites and diffusion mechanism of alkylbenzenes in large pore zeolite catalysts as predicted by molecular modeling techniques[J].Journal of Catalysis,1998,174:88-97.
[64]Waghmode S B,Bharathi P,Sivasanker S,et al. Molecular modeling studies on zeolites catalyst s for shape-selective electrophilic substitution:Formation of xylenes[J].Microporous Mesoporous Materials,2000,38(2-3):433-443.
[65]代振宇,邵潜,李阳,等. FCC汽油模型化合物在不同分子筛中扩散行为的分子模拟[J]. 石油学报,2007,23:41-45.
[66]Christ C D,Mark A E,van Gunsteren W F J. Basic ingredients of free energy calculations:A review[J].Comput. Chem.,2010,31:1569-1582.
[67]Laio A,Gervasio F L. Metadynamics:A method to simulate rare events and reconstruct the free energy in biophysics,chemistry and material science[J].Rep. Prog. Phys.,2008,71:126601.
[68]Nishihara Y,Hayashi S,Kato S. Theoretical study of CO escaping pathway in myoglobin with the 3D-RISM theory[J].Chem. Phys. Lett.,2008,464:220-225.
[69]Bocahut A,Bernad S,Sebban P,et al. Relating the diffusion of small ligands in human neuroglobin to its structural and Mechanical properties[J].J. Phys. Chem. B,2009,113:16257-16267.
[70]Dubbeldam D. Snurr R Q. Recent developments in the molecular modeling of diffusion in nanoporous materials[J].Molecular Simulation,2007,33(4-5):305-325.
Research progress of molecular simulation of diffusion in zeolites
LIU Lifeng,ZHAO Liang,CHEN Yu,GAO Jinsen
(State Key Laboratory of Heavy Oil Processing,China University of Petroleum(Beijing),Beijing 102249,China)
The diffusion in zeolites by using molecular simulation methods has become a new technology in recent years. Molecular simulation technique has contributed to greatly accelerated research on catalysis in a cost-effective manner. Typical methods of molecular simulation are reviewed. Molecular simulation of diffusion in zeolites are introduced in detail,including diffusion coefficients,inffluence factors of diffusion coefficients,application of diffusion interaction energy and transition state theory. In addition,the trend and challenges of molecular simulation technique in heterogeneous catalysis are also discussed.
molecular simulation;zeolite;diffusion coefficients;diffusion interaction energy;transition state theory
O 641;TQ 021.4
A
1000–6613(2011)07–1406–10
2010-10-11;修改稿日期:2010-11-26。
国家自然科学基金(20906102)及中国石油大学(北京)引进人才科研启动基金(BJBJRC-2010-2)项目。
刘立凤(1985—),女,硕士研究生。E-mail liulifenger@126.com。联系人:赵亮,副研究员。E-mail liangzhao@cup.edu.cn。
