两个专属渔业资源区的离散动力学模型分析

顾恩国,梁 艳,范致鉴,廖容云

(中南民族大学数学与统计学学院,武汉430074)

两个专属渔业资源区的离散动力学模型分析

顾恩国,梁 艳,范致鉴,廖容云

(中南民族大学数学与统计学学院,武汉430074)

假设渔业资源分属于两个区域,建立了一个渔业资源储量-捕捞力度动态模型,用聚合方法得到了一个简化的动力系统,定量分析了正不动点的存在性、稳定性和局部分叉,并用数值模拟验证不动点的局部分叉.最后,用全局分析方法来描述资源在什么范围可持续利用.

储量-捕捞力度动态模型;时间刻度;聚合方法;正平衡点的稳定性;分叉;可行吸引域

随着人口的增长和经济的发展,公共渔业资源的过度捕捞已严重影响其再生能力和人类对它的可持续利用[1,2],因此再生资源的可持续利用已成为重要的研究课题.众所周知,公共渔业资源的可再生能力的演化是一个复杂的非线性过程,它不仅与资源的自然环境因素(生物种群的自然增长率,生存环境的自然承载能力)有关,还与社会因素有关(市场的价格,捕捞者的捕捞能力和捕捞社会成本)有关.在国内外,关于渔业资源可持续发展的研究很多,许多学者已建立了许多数学模型,大多是在微分方程的基础上提出的不同区域渔业资源的动态和捕捞力度模型[3,4],很少用离散动态模型对其演化进行全局分析,尽管有人已经提出关于时间演化的鱼的数量和捕捞力度的离散模型[5,6],但很少有考虑在不同的时间刻度下捕捞力度的时间演化[7].因此,本文要利用两个时间刻度的存在性,假设渔业资源分属于两个区域,每个区域各有一个船队进行捕获,鱼在两区域内的游动比资源增长速度快,渔船的移动速度比船只数目变化快.在快的时间刻度下,全部渔业资源和船只的数目保持不变,在此条件下构造的离散动力学模型,这个模型描述鱼的储量和捕捞力度随时间演化的规律.用来弄清当前渔业资源在什么范围才能保持不枯竭,能够为资源管理者提供参考.

1 模型的建立

我们主要考虑两个相连渔业区域鱼的密度分别为x1,x2,捕捞力度分别为E1,E2,为了简单化,我们假设所有的渔船的捕捞时间相同,这样在每个区域的捕捞力度都能测量.我们假设这两个过程发生在两个不同时间刻度,捕捞的总数和船的总数保持不变,这里的r和E分别表示第i个区域自然增长率和承载能力.对于捕捞力度要根据收入的多少而变化.这里c是第i个船的捕捞成本,p是鱼的市场价格,假设是常数.根据前面的假设,建立系统如下:

式中qi(i=1,2)为个体i的捕捞能力,aij表示鱼从区域i到区域j的迁移率,bij表示渔船从区域i到区域j的迁移率,N≫1是鱼和船每年或每个季节或每个月迁移的次数,假如我们令∈=1/N,方程(1)可以被写成下列形式:

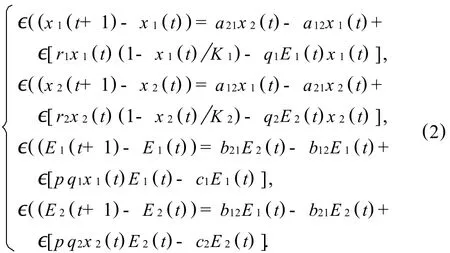
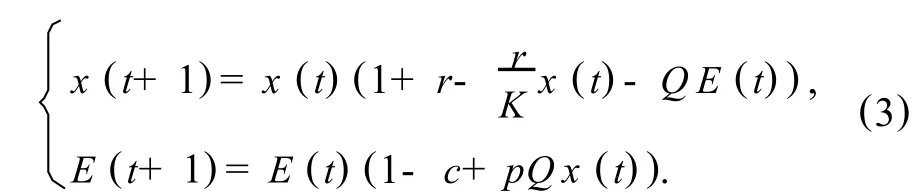
2 正平衡点的存在性

根据(3)式可以写成映射动力系统形式:

下面求系统(4)的不动点,基于模型本身的意义,不动点应为正值,系统(4)的不动点满足x′=x,E′=E,即系统(4)的均衡点应是下面非线性方程的解:

很显然,系统(5)有两个边界平衡点E0(0,0),E1(K,0),并且有唯一的正平衡点P(x＊,E＊),这里其中满足点P是正平衡点.

3 正平衡点的局部稳定性和分叉

系统(4)的稳定性,主要取决于系统(4)的Jacobian矩阵的特征值,该矩阵在平衡点(x,E)有如下形式:

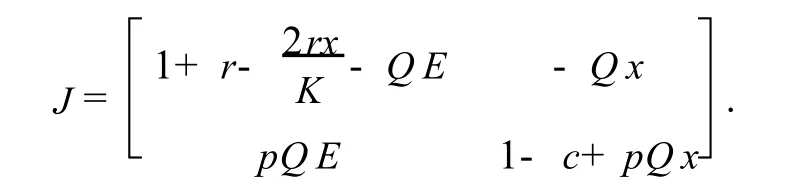
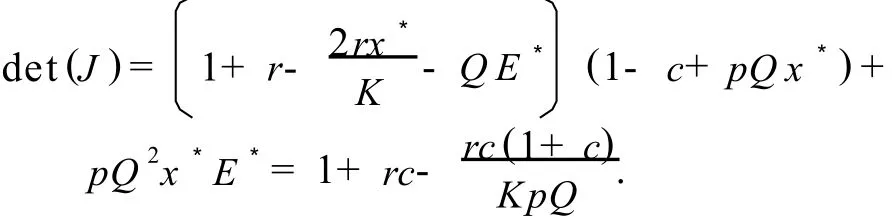
它的特征方程表示为P(λ)= λ2-tr(J)λ+det(J)=0,根据非线性动力系统方法可知,当正平衡点P稳定时,特征方程的根需满足｜λ｜＜1,即满足Jury条件[8].

定理1对P(λ)= λ2-tr(J)λ+det(J).

(ii)当P(1)=0时,即系统(4)在正平衡点P处将产生fold分叉;

(iii)当P(-1)=0时,即系统(4)在正平衡点P处将产生flip分叉;

(iv)当P(0)=1时,即系统(4)在正平衡点P处将产生N eimark分叉.

为分析正平衡点的稳定性,现利用数值模拟方法给出系统在一定初值下关于K的一维分叉图.为了便于计算,我们假设两个区域的渔船和市场价格相同,令c1=c2=c,α1β1=m,α2β2=n,Q=q(m+n),下面作定性分析,我们固定参数K=3.5,r=2,m=0.3,n=0.2,q=0.8,p=1,c=1,系统(4)将有一个正的稳定的平衡点P(2.5,1.43)且P(-1)=0.571,P(1)=1.714,P(0)=0.877.

我们对这个动力系统进行初步分析,图1为初始渔业资源,x0=2.51,E0=1.4时关于参数K增加的分叉图,系统参数r=2,c=1,q=0.8,p=1,m=0.3,n=0.2.从图1可以看出,它包含周期合并和很多窄的周期窗口,但是不包含明显的倍周期分叉和宽的周期窗口,并且还表明有切分叉现象,它表现为系统的间歇混沌和超级间歇混沌现象.间歇的特点是尽管所有的控制参数是常数并且没有外部干扰的情况下系统仍在规律和混沌行为之间切换.当K=2.5时,正平衡点发生切分叉.2.5＜K＜5时,正平衡点稳定,表明渔业资源稳定在一个正值,当K＞5时,正平衡点失去稳定产生N eimark分叉,当K＞5.9时,产生七周期点,再经过周期分叉渔业资源最后达到混沌状态,即资源在一定范围内产生随机波动.

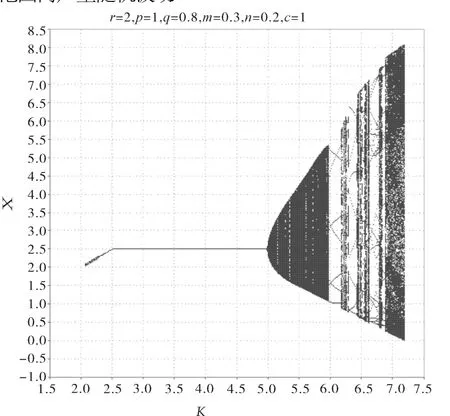
图1 系统(4)关于承载能力K的一维分叉图Fig.1 One-dimensional bifurcation diagram of the system(4)w ith respect to the carrying capacityK

4 正平衡点的全局分析

资源可持续利用的正平衡态的可行吸引域的形状和大小的研究对于弄清渔业资源的当前储量是可以得到维持再生能力还是最终导致资源枯竭的条件在可再生资源的研究中起着关键作用.本文用数值模拟来分析其吸引域结构[9,10],即研究所有吸引域包含在R2+={(x,E)｜x≥0,E≥0}中的x和E满足初始条件.假如鱼的密度是负值,鱼资源处于灭绝状态,通过数值试验我们可以知道,随着环境承载能力的增大可行域将增大.图2系统参数r=2,c=1,p=1,q=0.8,m=0.3,n=0.2,当2.5＜K＜5时,正平衡点是稳定的,表明渔业资源稳定在正平衡点附近,随着K的增大,正平衡点通过N eimark分叉失去稳定产生准周期吸引子,再经过一系列周期分叉以后,渔业资源达到混沌状态,即资源在一定的范围内随机波动.在图2(a)中有一个正平衡点P(2.5,1.43),点P的可行域用藏青色区域D来表示,不可行域用黄色区域C(D)表示,吸引子用红色表示.尽管在图2(a)-(d)的可行域结构都是三角形,它随着K的增大而增大,但是在图2(e)-(f)中吸引域已不再是三角形,但K达到一定数值时,吸引域边界变得越来越复杂,最终会使吸引域不存在,也就意味着资源的灭绝.可行域的边界是由两坐标轴X={(x,E)｜E=0,(x,E)∈R2+}和E={(x,E)｜x=0,(x,E)∈R2+}以及它们的任意阶前像构成.X和E的前像X-1:根据上面的参数值可知,双曲线E-2其中一支在第三象限即不在可行域内,另一支在第一象限可行域内,且在K＜6.5远离E-1,随着K的增大,E-2越来越接近E-1,当K=6.66时,两曲线发生接触,可行域发生变化不再是三角形,吸引子也从周期点变成混沌吸引子,所以吸引域的边界是由X-1,E-1,E-2所界定,E-1交X轴和交E轴(0,7.5),很容易得到三角形的面积当2.5＜K＜6.66时,随着K的增大,可行域的面积在增大,吸引子发生很明显的变化,首先从平衡状态到准周期到七周期再到混沌吸引子,当K＞6.66时,吸引域变得比较复杂,当K=7.2时,混沌吸引子接近可行域边界即发生最终分叉,当K=7.208时,混沌吸引子此时变化成排斥子.可行域的结构变得更复杂.当K＞7.208时,混沌吸引子消失,吸引域不再存在,在这种情况下,自然环境的很小扰动在未来都会造成渔业资源的灭绝.

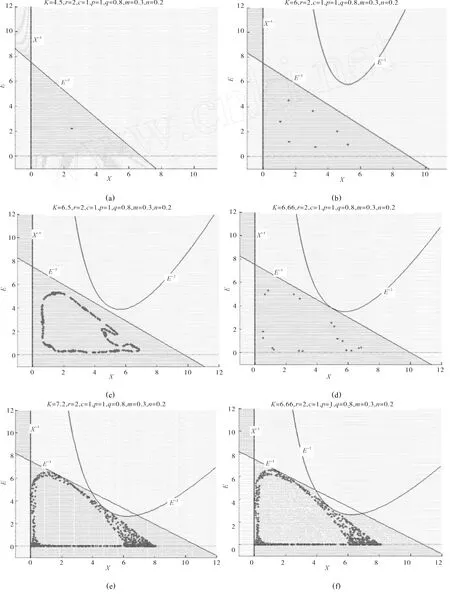
图2 系统(4)关于参数r=2,c=1,p=1,q=0.8,m=0.3,n=0.2随着参数K变化的可行域和最终分叉Fig.2 Feasible domains and final bifurcation of the system(4)w ith respect to the set of parametersr=2,c=1,p=1,q=0.8,m=0.3,n=0.2 and the ranging of parameterK

5 结语

本文提出的是两个专属渔业经济区的渔业资源的离散动力学模型,并且对模型进行了非线性分析,得到正平衡点的存在性和稳定性以及可行吸引域,从而揭示了渔业资源可持续利用的内在规律,描述了在一定的环境和社会因素下(即给定系统参数下)当前的资源储量在什么范围资源具有再生能力和处于什么范围会导致资源枯竭,从而对渔业资源管理决策者有效监控资源有参考意义.

[1] Food andA griculture O rganization.The state ofworld fisheries and aquaculture[R].Sofia:FAO,2004.

[2] Garcia,Grainger J R.Gloom and doom?The future of marine capture fisheries[J].Philosophical tanscations of the royal society,2005,B360:21-24.

[3] Clark C W.M athematical bioeconom ics:the opt imal management of renewable resources[M].N ew York:W ilery,1976.

[4] Bischi G I,KopelM,Szidarovszky F.Expectationstock dynam ics in multi-agent fisheries[J].A nnals of Operations Research,2005,137:299-300.

[5] Bischi G I,Szidarovszky F.Harvesting dynam ics in protected and unpretected areas[J]. Journal of Econom ic and O rganization,2007,62:384-370.

[6] Robinson R C.A n introduction to dynam ical system s:continuous and discrete[M].N ew Jersey:Pearson/Prentice Hall,2004:516-517.

[7] 顾恩国,褚青涛.不同理性两个体捕捞公共渔业资源的非线性分析[J].中南民族大学学报:自然科学版,2009,28(2):107-115.

[8] Gu Enguo.Global analysis of an ecological populationalmodelw ith an external interference[J].Chaos Solitions and Fractal,2007,32:224-233.

[9] Gu Enguo,Rung J.On some global bifurcations of domains of feasible trajections : analysis of recurrence equations[J]. Int J of Bifurcation and Chaos,2005,14(5):1625-1639.

[10] Gu Enguo.Global bifurcations of domains of feasible trajectories:analysis of a predator-prey model[J].Int J of Bifurcation and Chaos,2006,16(8):2601-2613.

Analysis of D iscrete Dynam icalM odel for Two Special Fishery Resource Zones

Gu Enguo,L iang Yan,Fang Zhijian,L iao R ongyun
(College ofM athematics and Statistics,South-CentralU niversity for N ationalities,W uhan 430074,China)

In this paper,fishery resources are supposed to be subdivided into two zones and a stock-effort dynam icalmodel is established.A dynam ical system is reduced by aggregation methods and quantitative methods are used to analyze the existence of positive fixed points,stability and local bifurcations,and numerical s imulation is used to verify the local bifurcations of fixed points.Finally,the globalmethods are used to analyze the extent of sustainable use of fishery resources.

stock-effort dynam icalmodel;t ime scales;aggregation method;stability of the positive equilibrium;bifurcation;feasible domain

F133.3

A

1672-4321(2011)01-0105-04

2011-01-13

顾恩国(1964-),男,博士,副教授,研究方向:非线性动力学应用,E-mail:guenguo@163.com

国家自然科学基金资助项目(10871209);中南民族大学自然科学基金资助项目(YZZ060277)