跳跃随机波动的阈值模型风险值的贝叶斯估计

王敬勇

（铜陵学院，安徽铜陵244000）

跳跃随机波动的阈值模型风险值的贝叶斯估计

王敬勇

（铜陵学院，安徽铜陵244000）

文章基于一类跳跃随机波动的阈值模型风险值估计贝叶斯分析，在给定先验分布下，以马尔科夫链蒙特卡洛方法估计模型中的未知参数，并给出了MCMC模拟算法，进而讨论了风险值的预测。根据模拟结果，我们得知，如果没有考虑金融时间序列的外生冲击导致的跳跃行为，将会高估风险值，因此考虑跳跃行为后，将增加风险值估计的精度。

风险值；阈值模型；随机波动模型；跳跃；MCMC

VaR(value at risk)技术是日前市场上最流行、最有效的风险管理技术，已成为国际金融市场主流的风险度量标准。VaR可以定义为资产报酬的分布p分位数，用公式表示为。实际应用上，比较感兴趣的是p值很小的风险值，如p≤0.05。为了达到准确估计VaR的目的，Chang et al（.2003）[1]指出，当为对数报酬率时，VaR估计较好。此外的分布对VaR的估计也有影响，一般假设服从扩散过程（diffusion process），。其中为波动率。对于金融时间序列，资产报酬一般具有厚尾性、波动集聚性和波动共移性。Taylor（1982）[2]提出的随机波动模型（stochastic volatility model简称为SV模型）可以很好的描述上述特性。

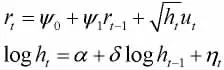
但是，影响资产报酬率的因素时刻都在变，故其分布的参数也是不断变化的，用静态的模拟方法不能得到有效的参数估计。针对这一缺陷，本文引入马尔科夫链蒙特卡洛MCMC模拟方法进行参数估计，同时兼顾了经验信息和观察到的样本信息，这样计算的值将更加准确。

1.跳跃随机波动的阈值模型

金融时间序列经常具有不对称性，即好消息与坏消息的冲击的影响不同。So,Li and Lam（2002）[3]将不对称性引入随机波动模型，提出随机波动的阈值模型。考虑阈值为0，使得在对数报酬率为正和负值时分别具有不同的随机波动模型。但实际的金融市场中，这种不对称性的阈值不一定为0，因此更一般的阈值可以假设为一未知常数。但在金融市场中时常受到外生冲击，出现随机跳跃现象，Hsieh and Tauchen（1997）[4]，Andersen,Benzoni and Lund（1999）[5]都发现了股票报酬存在着随机跳跃行为。因此对于既能很好描述金融时间序列特性、又能反映金融市场的杠杆效应和外生冲击的一类风险值估计，将能更好地对风险值进行预测。这时模型为，

2.MCMC算法

为了使运算过程较简易，参照So,Li and Lam（2002）[7]，将参数做转换，令，

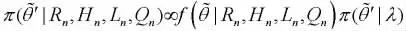
3.风险值估计

假设股价对数报酬率符合跳跃随机波动的阈值模型，在给定数据Rn以及参数的先验分布下，若为的后验分布，则在时间t时，的密度函数为，

4.模拟结果与分析

根据模拟资料，给定超参数的先验分布，利用MCMC算法求模型中参数的近似贝叶斯平均数，近似后验标准差与95%的置信区间以及新一期报酬率的风险值。本文所有风险值的模拟迭代次数为100000。

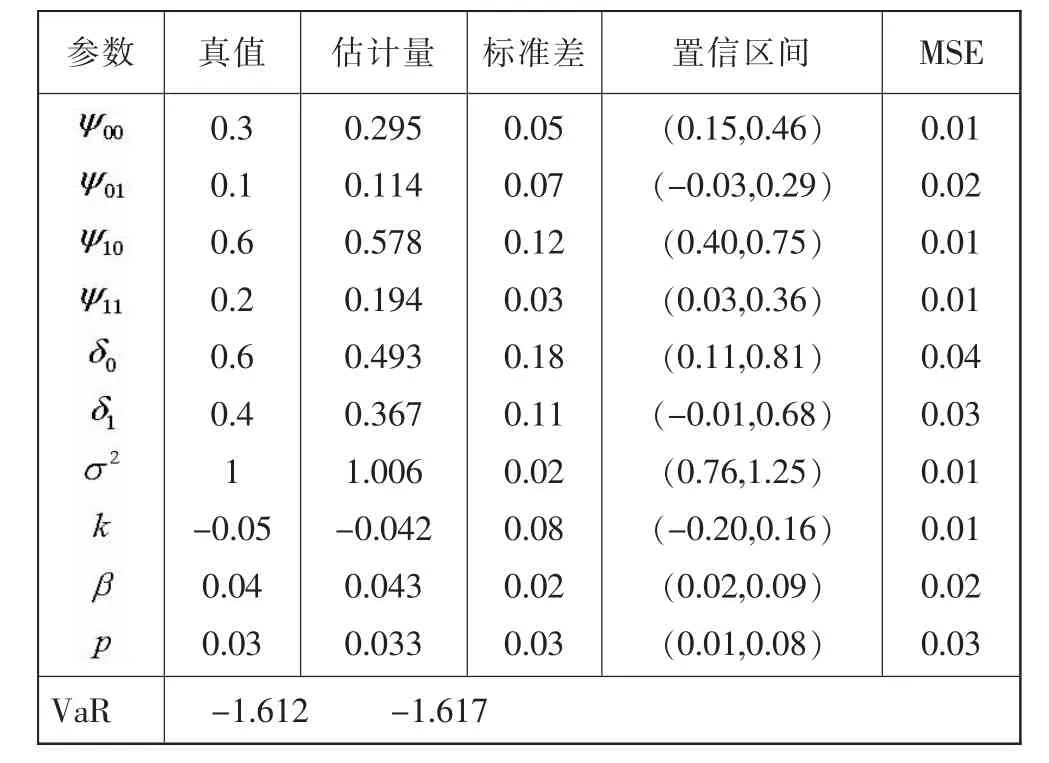
表1 贝叶斯估计的MCMC模拟结果

为了作一比较，使用同样的模拟估计方法，对没有跳跃的随机波动的阈值模型的VaR进行了估计（省略了估计结果），最终的VaR估计结果为-1.627。从中可以看出如果没有考虑跳跃因素，将会高估风险，主要因为没有考虑跳跃的随机波动的阈值模型分布尾部不足反映具有跳跃模型的真实分布。同时，为了比较没有跳跃和考虑跳跃因素的VaR估计的两种模型哪个更加合理，使用Spiegelhalter（2002）所提出的偏差信息准则（DIC）进行模型选择，其中DIC又称为广义的AIC，其表示偏差的后验分布期望值加一个惩罚项，即

表2 偏差信息准则

5.结论

本文基于一类跳跃随机波动的阈值模型VaR的MCMC模拟估计，模拟结果显示当模型中存在随机跳跃行为时，若不考虑外生冲击带来的跳跃行为，将会高估风险，可能会造成对股票投资的不确定性。另外本文只考虑了资产报酬率模型的正态性假设，而t分布或许比正态更有效。

［1］Chang,Y.P.,Hung,M.C.and Wu,Y.F.Nonparametric estimation for risk in Value-at-Risk estimator[J].Communications in Statistics:Simulation and Computation.2003,(32):1041-1064.

［2］Taylor,S.J.Financial returns modeled by the product of two stochastic processes,a study of daily sugar prices 1961-79[J].In Time Series Analysis:Theory and Practice 1,Anderson,O.D.(ed.).North-Holland:Amsterdam.1982.203-226.

［3］So,M.K.P.,Li,W.K.and Lam,K..A threshold stochastic volatility model[J].Journal of Forecasting.2002,(21):473-500.

［4］Hsieh,G.D.and Tauchen,G.Estimation of stochastic volatility models with diagnostic[J].Journal of Econometrics.1997，(81):159-201.

［5］Andersen,T.G.,Benzoni,L.and Lund,J.An empirical investigation of continuous-time equity returns models[J].Journal of Finance.1999，(57):1239-1294.

［6］Andersen,T.G.,Bollerslev,T.,Diebold,F.X and Ebens,H.,The distribution of realized stock return volatility[J].Journal of Finance.2001,(61):43-76.

［7］Qian Yan cheng.Threshold stochastic volatility jump model bayesian inference[D].Master’s thesis,National Central university.2007.

Bayesian Estimation on Jump Stochastic Volatility Threshold Model of VaR

Wang Jing-yong
（Tongling University,Tongling Anhui 244000，China）

This paper develops a class of jump stochastic volatility threshold model of VaR Estimation from a Bayesian viewpoint.Bayesian inferences of the unknown parameters are obtained with respect to a subjective prior distribution via Markov chain Monte Carlo(MCMC)method,MCMC algorithm and the value at risk(VaR)predictive are also developed.Based on simulation,if the jump is not Considered,the value at risk is overestimated.The precision of value at risk estimation is increased.

value at risk;threshold model;stochastic volatility model;jump;Markov chain Monte Carlo

F830

A

1672-0547（2011）01-0021-02

2010-09-15

王敬勇（1978-），男，安徽淮北人，铜陵学院经济贸易系讲师，博士，研究方向：管理科学与工程。