基于分目标乘除法的双目标投资组合模型

邓 雪，赵俊峰，李荣钧

Markowitz[1]于1952年最早提出了关于投资组合的均值-方差模型，它是金融投资定量化研究的开端，成为金融投资理论研究的主要论题和决策实践的重要工具。在该模型中，用预期收益来衡量投资组合的收益，用预期收益的方差来衡量投资组合的风险。Sharpe[2]和Perold[3]研究了如何求解均值-方差模型，并提出了一些解决有效投资组合问题的手段和算法。陈国华[4]等用区间数来描述证券的期望收益率和风险损失率，建立区间数模糊证券投资组合模型，利用区间数知识把区间规划问题转化为参数线性规划问题进行求解。罗党[5]等以灰色系统理论和概率论为基础，探讨了含有区间数的组合投资决策问题，提出了具有交易费用的灰色组合投资模型的有效解及其临界最优解和均值化最优解的概念。而本文是在基于Markowitz投资组合的均值-方差理论下，构建一个投资组合预期收益率在一定范围的双目标混合投资组合摸型，同时采用分目标乘除法来求解该模型。一实际算例表明：本文所构建的模型和所采用的方法是有效的。

1 双目标投资组合模型

假设投资者选择了n种可投资的风险资产进行组合投资。为方便起见，记：

R=[r1r2…rn]T是风险资产的期望收益向量；

V=(σij)n×n是风险资产收益的协方差阵；

x=[x1x2…xn]T是风险资产的投资比例向量；

l=[1 1…1]T是分量全部为1的向量；

L,U分别表示投资比例向量的下限和上限．

这里，（T）表示矩阵的转置，所有不带有（T）的向量都是列向量，那么资产组合的期望收益是r(x)=RTx，风险是σ2(x)=xTVx。要求投资者的期望收益达到μ以上，那么可以构建如下的双目标投资组合模型：

2 分目标乘除法介绍[6]

2.1 分目标乘除法基本思想

双目标混合最优化模型如下：

其中，X为可行域．分目标乘除法的主要特点是：将模型中的各分目标函数进行相除处理后，在可行域上进行求解。为了使模型（2）中的目标函数 f1(x)极小化，f2(x)极大化，可以考虑让目标函数 f2(x)的倒数极小化。因此，求解模型（2）可以归结为求解在可行域X上极小化乘除分目标函数，即求解

的问题。由上述数值极小化问题所得的最优解，显然是使位于分子的目标取尽可能小的值，并且使位于分母的目标取尽可能大的值。

表1 参数μ的不同取值的最优解

以上方法实际上是对模型（2）构造了评价函数

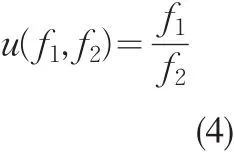
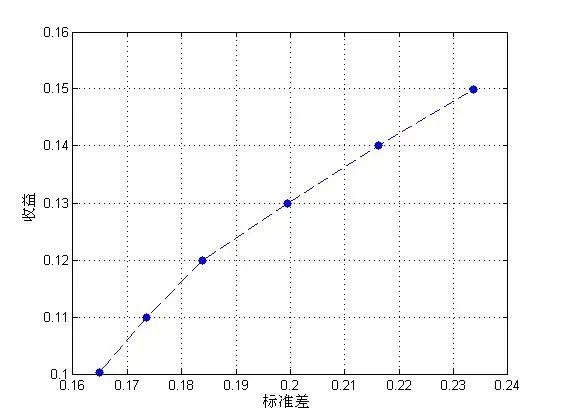
图1 投资组合模型（6）的有效边界

为了使（4）是有意义的，一般要求各目标函数在可行域X上均取正值。上述利用分目标相除来求解模型（2）的方法叫做分目标乘除法。

模型（1）中的两个分目标函数都是取正值的。分目标乘除法运用在模型（1）的求解上的经济意义为：单位收益所承受的最小风险。

2.2 分目标乘除法计算步骤

Step1:分目标乘除法．检验各目标函数在可行域X上是否取值为正。若大于零，则进行step2；否则，选取某实数M＞0，使

并令 fi(x):=fi(x)+M(i=1,2)，进行step2．Step2:极小化分目标乘除问题。求解模型（3）

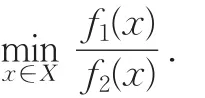
的最优解为x，则x即为模型（2）的有效解．

3 应用研究

现考虑5种证券的投资组合问题，其收益率的协方差矩阵为：

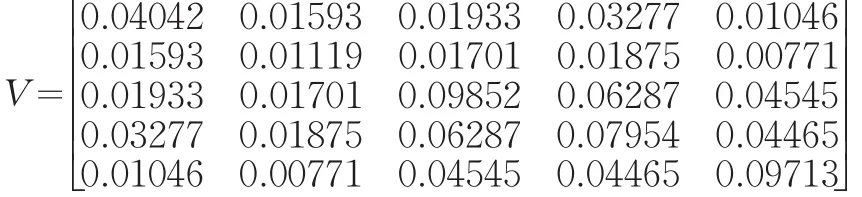
其中，

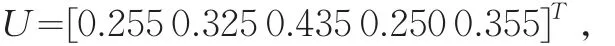
要求投资组合预期收益达到μ以上。那么应用模型（1），得到如下的双目标规划模型（5）。再根据分目标乘除法来求解上述模型：

Step1:分目标正值化：根据实际意义，分目标函数在定义域上取值均大于零。

Step2:极小化分目标乘除问题。求解模型（6）．

对于参数μ的不同取值，可得不同的最优解x（见表1）。根据表1中的数据，可得模型（6）的有效边界（见图1）。

4 结论

本文构建了一个双目标投资组合模型，并采用分目标乘除法求解该模型。最后给出一具体算例表明本文构建的模型和所采用的算法是有效的，其经济意义为：单位收益下的风险极小化。并且对于预期收益参数μ的不同值，有不同的最优解。

表1的数据表明：

（1）当μ≤0.10时，得到的最优解和对应的收益和风险值是不变的，即：

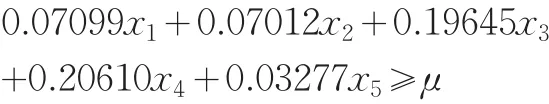
这个约束条件为冗余条件，对于求解没有限定意义的。

（2）当μ≥0.16时，在可行域范围内没有可行解。

（3）当μ在0.11和0.15之间取不同的值时，有不同的最2优解。并且当μ变大时，目标函数 ，风险σ，标准差σ，收益r都在变大，即都为μ的增函数。

（4）当μ=0.13,0.14,0.15时，x1=0.0550和x5=0.1850都达到了投资比例的下限，而x4=0.2500达到了投资比例的上限。

（5）当μ=0.11,0.12时，x2=0.3250达到了投资比例的上限，而x5=0.1850达到了投资比例的下限。

图1表明模型（6）的有效边界：随着标准差σ的增加，收益r也在增加。并且图1中的有效边界类似开口向右的半根抛物曲线。

[1]Markowitz H.Portfolio Selection[J].Journal of Finance,1952,（7）.

[2]Sharpe W F.Capital Asset Process:a Theory of Marker Equilibrium Under Condition of Risk[J].Journal of Finance,1964,（19）.

[3]Perold A F.Large-scale Portfolio Optimization[J].Management Science,1984,（30）.

[4]陈国华,陈收,汪寿阳.区间数模糊投资组合模型[J].系统工程,2007,25(8).

[5]罗党,陈东升.一类灰色组合投资决策方法[J].数学的实践与认识,2005,35(5).

[6]胡毓达.实用多目标最优化[M].上海：上海科学技术出版社，1990.