我国货币供给量与股票价格之间协整关系的稳定性研究

毛彦军

（西安交通大学 经济与金融学院，西安 710061）

0 引言

通过构建时间序列模型研究经济问题时，经常遇到的一个潜在问题是模型中参数估计值具有不稳定性，也即是说模型中的参数估计可能随着样本区间的不同而改变。然而，一旦模型中参数呈现出不稳定性，时间序列模型就会有误设的嫌疑，这将为后续的统计推断和政策研究带来严重后果。目前，国内外学者已对此开展了深入研究，并把这一研究归类为寻找时间序列的结构断点问题。关于参数估计的不稳定性问题，不仅仅出现在简单的时间序列回归模型中，涉及时间序列参数估计的多数研究中，都存在类似的“结构断点”现象。因此，对此问题进行探索性研究具有很强的现实和理论意义。本文受Hansen[13]研究启发，采用Phillips-Hansen完全修正估计方法对我国样本期为2000年2月至2009年12月的货币供给量（M2）和股票价格进行协整关系的稳定性检验。本文之所以关注货币供给量与股票价格之间的协整关系稳定性，主要处于以下考虑：货币政策与股票价格之间的关系一直是是理论界与实务界关注的一个热点，这关系到货币政策的有效实施和宏观经济的稳定。同时，我国目前还没有实现利率市场化，货币政策中介目标主要是货币供给量（M2）。在研究货币政策与股票价格之间的关系文献中，多采用货币供给量（M2）作为货币政策实施的有效变量，来研究M2与股票价格之间的协整、因果以及脉冲响应等关系为货币政策的实施提供建议。从既有的文献研究过程来看，通常在运用Johansen协整检验法给出协整关系检验结果后就进入了下一步分析，这忽略了存在不稳定协整关系的可能性。事实上，随着社会体制的改革，货币政策和股市政策等的重大变化完全有可能改变这种协整关系，也就是说协整关系会出现一处或多处结构变化。为此，本文将关注于货币供给和股票价格之间的协整关系稳定性问题，这将有助于提升相关研究的可靠性，为宏观政策的出台和实施提供有益的参考。

1 Phillips-Hansen完全修正估计方法

遵循Phillips和Hansen的做法，构建如下多元回归方程：

其中zt=(k'1t,x't)'由下列方程确定

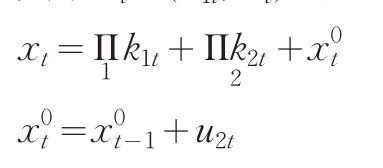
并且k1t，k2t为非负整数，u1t，u2t为两列白噪声过程。

在随后的研究中，Hansen对方称(1)进行了修正，使原有模型包含了参数不稳定因素，即允许方程系数A随时间而发生改变，修正后的模型为

对于修正后的方程系统，Hansen称之为协整方程，在k1t为常数的情况下，Hansen给出了检验两个单整时间序列yt和xt协整关系稳定性的三个检验统计量。规定零假设H0：At为常数，即协整关系稳定；备择假设H1：At变化，即协整关系不稳定。三个检验统计量具体构成如下：

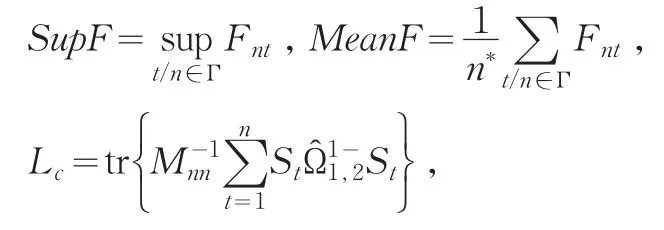
其中Γ为(0,1)上的紧集，

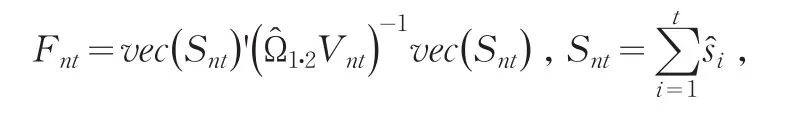
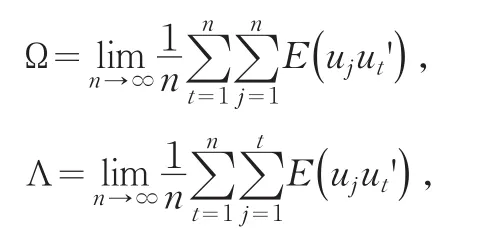
分块矩阵的表达式为：

Andrews用Γ表示搜索域，并且指出Γ不能包含端点值0和1，如果包含这两个端点值，统计量将几乎必然的发散到无穷远，并且建议Γ的取值为[0.15,0.85]。本文在第三部分的实证检验过程中，将采用Andrews的建议值。

以上给出的三个检验统计量SupF，MeanF，Lc，它们有相同的零假设，而备择假设具体表现形式不同。另外，三个统计量都有自己最佳检验目标：如果检验整个时间过程是否存在区制转移，选取SupF是最优的；如果是检验一个模型是否为一个包含了稳定关系的好模型，选取MeanF是最优的；如果待检验的方程中参数变化的极大似然值在整个样本空间中相对恒定性，选取Lc是最优的。同时，在这三个统计量中，Lc还具有便于计算的优点。鉴于统计量的这些特点和模型检验的固有不确定性，本文依据三个统计量分别对我国货币供给量和股票价格之间的协整关系进行稳定性检验。检验过程将选取Hansen[13]中给出的临界值，这些临界值是由Hansen通过对大小为1000的样本进行25000次蒙塔卡罗模拟得到，具有很高的精确性。

2 数据选取与实证结果

本文研究的样本选取为2000年1月至2009年12月的我国货币供给量和上证指数的月度数据，数据来源为中国人民银行网站和Wind咨询。由于所选取的数据均是月度数据，具有明显的季节波动性，所以用X11方法对两列数据进行季节性调整以消除季节性波动的影响。同时，为消除宏观时间序列数据波动的异方差性，对调整后的货币供给量和股票价格指标均取自然对数，分别记为Lnm，Lns。

2.1 协整关系检验

对时间序列进行协整关系检验时，相应序列必须满足同阶单整。所谓同阶单整是指若干个非平稳的时间序列经过相同阶差分后变成平稳序列的特性。下面将采用常用的ADF检验方法对所选取的时间序列进行平稳性检验。时间序列平稳性检验结果如表1所示。

由表1我们可以看出序列Lnm，Lns存在单位根，属于非平稳序列，而对应的一阶差分序列DLnm，DLns不存在单位根是平稳序列，这说明货币供给量和股票价格序列满足一阶单整过程，可以对两变量进一步做协整关系分析。

表1 序列的平稳性检验

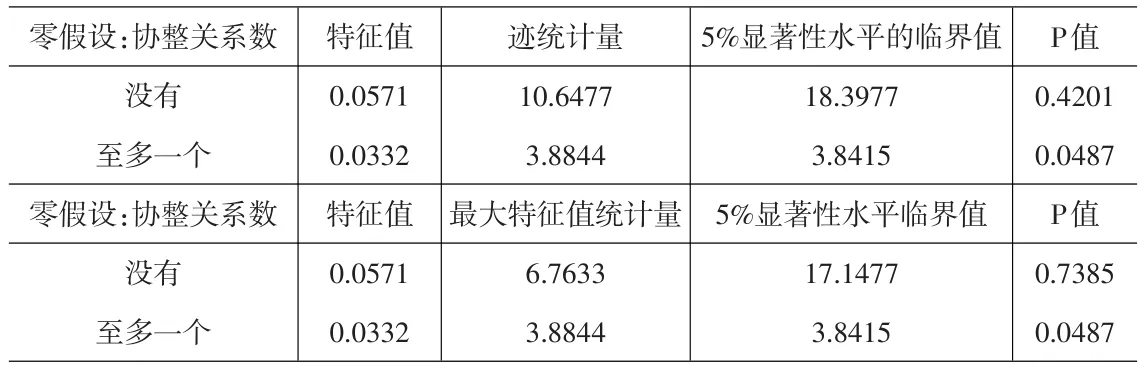
表2 Johansen协整关系检验

下面运用Johansen的检验方法对Lnm，Lns进行协整关系检验。Johansen协整关系分析法实际上是一个循环过程，主要依靠以下两个检验统计量进行实证分析。

Trace统计量（迹统计量）：

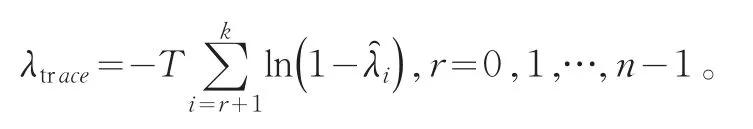
Maximal Eigenvalue统计量（最大特征根值统计量）：

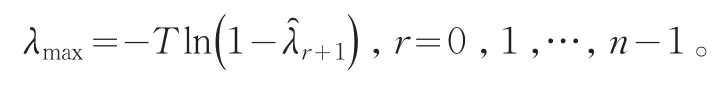
其中表示货币供给量和股票价格组成的VAR系统的系数矩阵的特征根的估计值，T表示有效的样本大小。如果统计量λtrace或者λtrace显著不为0，那么就拒绝对应的原假设。

下面分别给出检验结果见表2。

表2是利用Johansen协整关系检验法对货币供给量与股票价格进行协整关系检验的结果。从结果中我们可以看出无论是迹统计量还是最大特征值统计量均能在5%的显著性水平下拒绝原假设，这就意味着我国货币供给量与股票价格之间存在协整关系。

2.2 协整关系稳定性检验

变量之间虽然存在协整关系，但是这种协整关系在整个样本区间是否稳定，需要我们作进一步的考证。这是因为随着政治体制改和货币政策的变化以及股市相关政策的调整等，变量之间的协整关系可能会出现结构变化。下面，我们首先直观分析一下存在协整关系的两时间序列走势（见图1）。

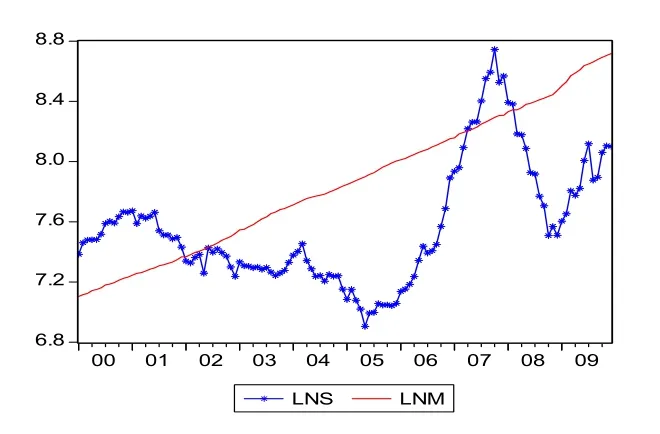
图1 货币供给量和上证综合指数自然对数序列走势

表3 协整关系稳定性检验结果

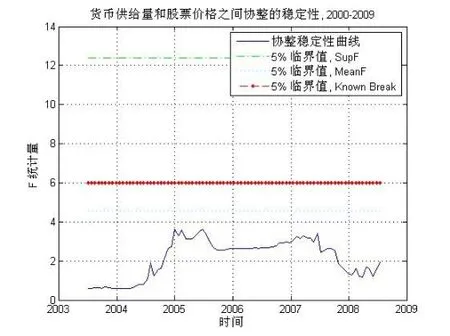
图2 协整稳定性检验曲线

在整个样本区间内，货币供给Lnm一直处于上升状态，上证综合指数Lns则存在一定的波幅，在前期小幅震荡走低后，迅速上升，达到顶点后开始折转下降。这暗示着，随着时间推移，两变量之间的协整关系可能出现结构变化，因此，对两变量之间协整关系的稳定性检验是必要的。

下面运用第二部分介绍的协整关系稳定性检验统计量SupF，MeanF，Lc对我国货币供给量和股票价格之间协整关系进行稳定性检验。需要说明的是，下面报告检验结果时，仅给出检验统计量和P值，并且借鉴Hansen做法，对于大于或等于0.2的P值，不报告具体的P值，只是在P值对应列标记≥0.2，反之将给出具体的P值。检验过程用到的临界值采用的是Hansen[13]给出的蒙塔卡罗模拟值。

由表3可以看出，SupF，MeanF，Lc三个统计量检验结果一致表明至少在20%的显著性水平下不能拒绝原假设，我国货币供给量和股票价格之间的协整关系具有很好的稳定性。

为了进一步考察协整关系的稳定性，下面给出凸显方程结构变化的F统计量序列的波动曲线。如果F统计量曲线穿过结构断点临界值标准线，意味着原有的协整关系发生了变化，这种变化可能来源于制度的改变或政策的调整。具体检验结果见图2。

上图中蓝色的实线为测度协整关系稳定性的F统计量曲线，标有红色圆点的直线表示存在稳定协整关系的临界值，如果F统计量曲线处在该临界值曲线下方，则表明变量时间的存在稳定的协整关系，否则，变量之间的协整关系就不稳定。如图2所示，2003～2009年间F统计量曲线一直处于临界值的下方，表明期间我国货币供给量与股票价格之间的协整关系比较稳定，货币政策对股市的作用相对比较平稳。

3 结论

本文考察了2000～2009年间我国货币供给量和股票价格之间协整关系以及协整关系的稳定性。结论表明：我国货币供给量与股票价格之间存在协整关系，并且这种协整关系不存在结构变化，比较稳定。

本文实证结论意味着，基于2000～2009我国货币供给量和股票价格数据研究二者之间长期均衡关系的协整分析和短期波动关系的误差修正模型不存在模型误设现象，分析结论是可靠的。另外，进入新世纪以来，我国货币供给量和股票价格维持这样一种稳定的长期均衡关系，也是我国货币政策作用于股市效果的一个直接体现。我们知道，2000年以后我国一些股市政策与货币政策交叉出台，二者相得益彰。例如2000年19月B股交易开放，2001年7月社保基金悄然入市，2001年11月下调股票交易印花税，这一系列的措施促使股价上涨，为抑制股价，央行从2003年9月开始连续10次上调准备金率，直至达到17.5%的历史高位。2004年10月25日保险资金获准直接入市，这无疑将对股价有上扬的冲击，为了阻止股价过度上扬，从2004年10月29日开始，央行进入了加息周期，从而货币供给量与股价呈现出稳定的均衡关系。同时，这种均衡关系折射出了我国货币政策的有效性，以及货币市场与股票市场运行的平稳性。

[1] Chow,G.C.Tests of Equality between Sets of Coefficients in Two Linear Regression[J].Econometrica,1960,28(3).

[2] Andrews,D.W.K.Tests for Parameter Instability and Structure Change with Unknown Change Point[J].Econometrica,1993,61(4).

[3] Chu,C.-S.J.New Tests for Parameter Constancy in Stationary and Nonstationary Regression Models[C].Working Papers 1989,University of California at San Diego.

[4] Hansen,B.E.Lagrange Multiplier Tests for Parameter Instability in non-linear Models[C].Working Papers,1990.

[5] Arestis,P.,Mariscal,I.B.Unit Root and Structural Breaks in OECD Unemployment[J].Economics Letter,1999,65(1).

[6] Ben-David,D.,Papell,D.Some Evidence of the Continuity of the Growth Process Among the G7 Countries[J].Economic Inquiry,2000,38,(2).

[7] Christiano,L.Searching for a Break in GNP[J].Journal of Business and Economic Statistics，1992,(10).

[8] Modigliani,F.，Cao,S.L.The Chinese Saving Puzzle and the Life-cy cle Hypothesis[J].Jounal of Economic Literature,2004,142(1).

[9] 张成思.通货膨胀动态路径的结构性转变及其启示[J].金融研究,2008,(3).

[10] 马双.中国居民储蓄率的内生断点分析：1953——2005[J].数量经济技术经济研究,2008,(7).

[11] 梁琪,腾建州.中国宏观经济和金融总量结构变化及因果关系研究[J].经济研究,2006,(1).

[12] Campbell,J.Y.,Shiller,R.J.The Dividend-Price Ratio and Expectations of Future Dividends and Discount Factors[J].Review of Fi nancial Studies,1988,(1).

[13] Hansen,B.E.Test for Parameter Instability in Regression With I(1)Processes[J].Journal of Business&Economic Statistic,1992,10(3).

[14] Phillips,P.C.,Hansen,B.E.Statistical Inference in Instrumental Variables Regression with I(1)processes[J].Review of Economic Studies,1990,57(3).