一种基于优势度的直觉梯形模糊数排序方法

王中兴，谢海斌

（广西大学数学与信息科学学院，广西南宁 530004）

0 引言

直觉模糊集和区间直觉模糊集[1,2]由保加利亚学者Atanassov提出，是对传统模糊集的一种扩充和发展。其在传统模糊集的基础上增加了一个新的属性参数——非隶属度函数,能够更加细腻地刻画客观世界的模糊性本质,在处理不确定信息时具有更强的表现力,所以（区间）直觉模糊集在学术界引起广泛关注[3～6]。文献[5,6,7]又从另一个方向对直觉模糊集进行了扩展，提出了直觉三角模糊数和直觉梯形模糊数的概念及其运算法则。直觉梯形模糊数使隶属度和非隶属度不再只是相对于一个模糊概念而是相对梯形模糊数,这更能准确反映决策者的信息。

目前,有关属性值为直觉梯形模糊数的多属性决策方法已经有了不少研究成果[7～13].而对直觉梯形模糊数进行排序是决策过程的一个重要环节,因此直觉梯形模糊数的排序指标成为许多学者研究的重点[9～13]。例如文献[9]利用直觉梯形模糊数的综合期望值区间数作为排序指标,根据区间数可能度法得到方案集的排序;文献[11]结合期望值给出直觉梯形模糊数的得分函数和精确函数的概念并把它们作为排序指标,得分函数大的直觉梯形模糊数也越大,若得分函数相等,则精确函数值大的直觉梯形模糊数较大,但是文献[9,11]给出的排序指标都只考虑了期望值这一单一因素,利用其排序有时会出现失效情况;文献[13]利用直觉三角模糊数的期望值和模糊度给出一种直觉三角模糊数的排序指标,克服了文献[9,11]中排序结果的失效性。本文将利用直觉梯形模糊数的期望值和散度给出一种新的排序指标,并与已有文献的排序指标进行比较,给出具体的实例分析。

1 直觉梯形模糊数的基本理论

定义1[8～11]设a是实数集上的一个直觉模糊数，其隶属函数μa(x)和非隶属函数νa(x)分别为

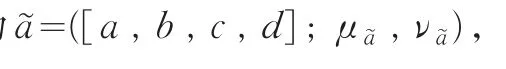
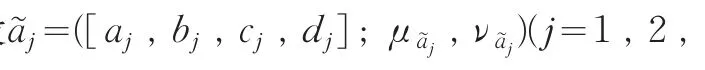
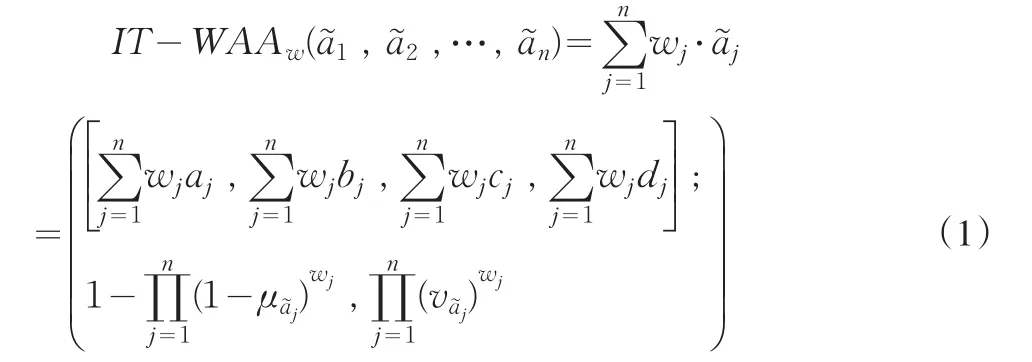
为直觉梯形模糊数的加权算术平均算子。其中,wj∈[ 0 , 1]，w1+w2+…+wl=1。

2 直觉梯形模糊数的排序指标

定义3[13,15,16]对于任意模糊数,其相应的α-截集为[La(α) ,Ra(α) ],α∈[0 ,w],w为的最大隶属度,则称

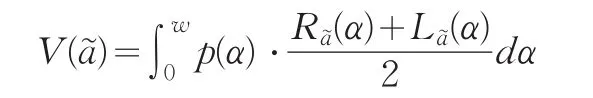
为模糊数的期望值,其中p(α)是对应的权重函数,满足如下条件：（1）p(α)在区间 [0 ,w]上是非负递增函数且特别是对于梯形模糊数则其相应的期望值为

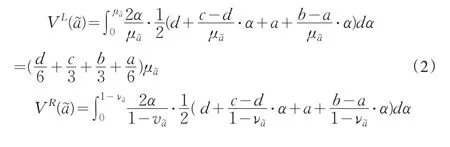
分别为直觉梯形模糊数的极小期望值和极大期望值。

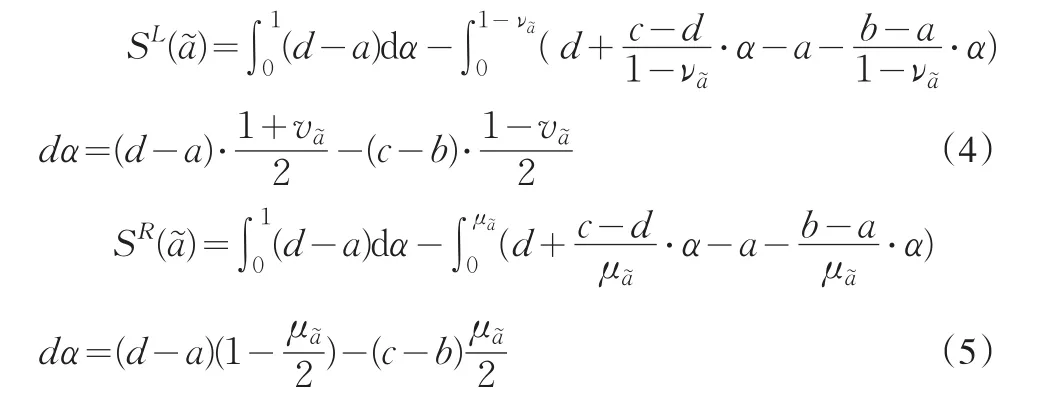
分别为直觉梯形模糊数a的极小散度和极大散度,如图1和2中阴影部分面积所示。

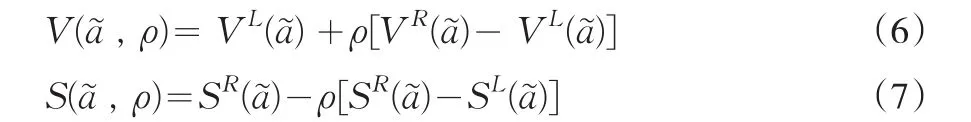
分别称为直觉梯形模糊数的期望值和散度.其中ρ表示决策者的态度,当时,表示决策者是悲观的;当时,表示决策者是乐观的;当时,表示决策者是中立的。

显然对于一个直觉梯形模糊数而言,当ρ确定，则V()越大,S()越小,则也越大,于是提出如下关于直觉梯形模糊数的一个排序指标。

为直觉梯形模糊数优势度。

显然,以优势度R,ρ)作为排序指标,R(,ρ)越大,则相应的直觉梯形模糊数a也就越大。为了说明本文所提出的优势度排序指标的有效性,选择如下三组直觉梯形模糊数将本文的排序指标与已有的一些排序指标进行比较。

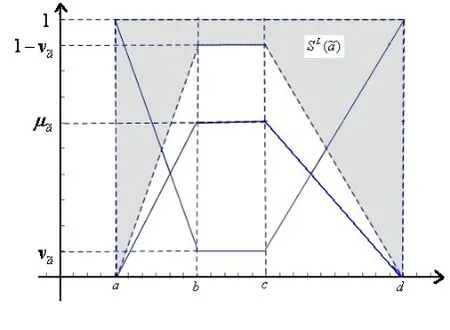
图1 直觉梯形模糊数的极小散度

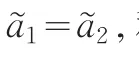
3 直觉梯形模糊数的多属性决策方法

针对权重信息确定且属性值为直觉梯形模糊数的多属性决策问题，本文根据直觉梯形模糊数的IT-WAAw集结算子和优势度指标可以得到最优方案排序，具体步骤如下。

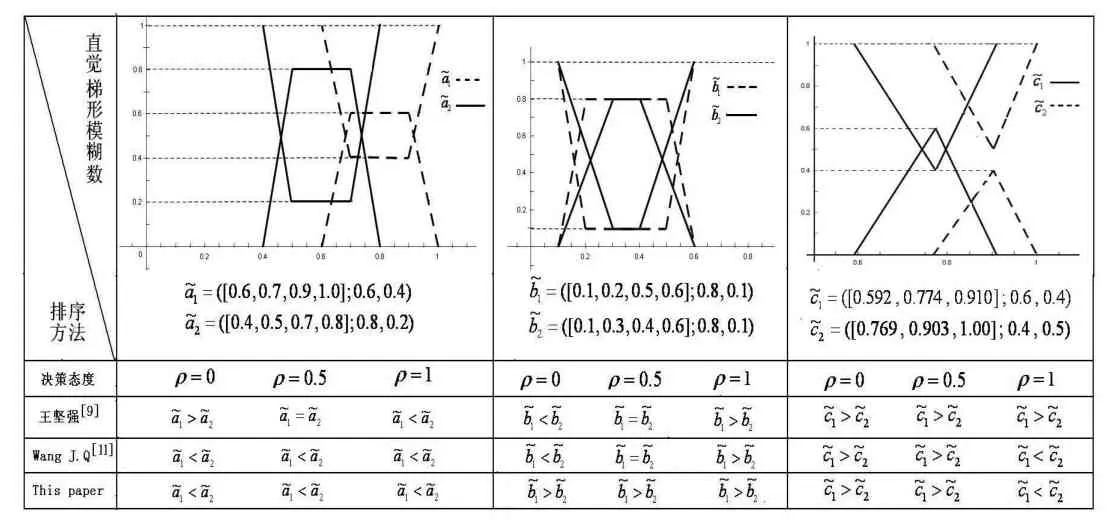
表1 几种排序指标得到的排序结果的比较

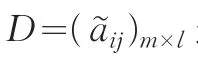
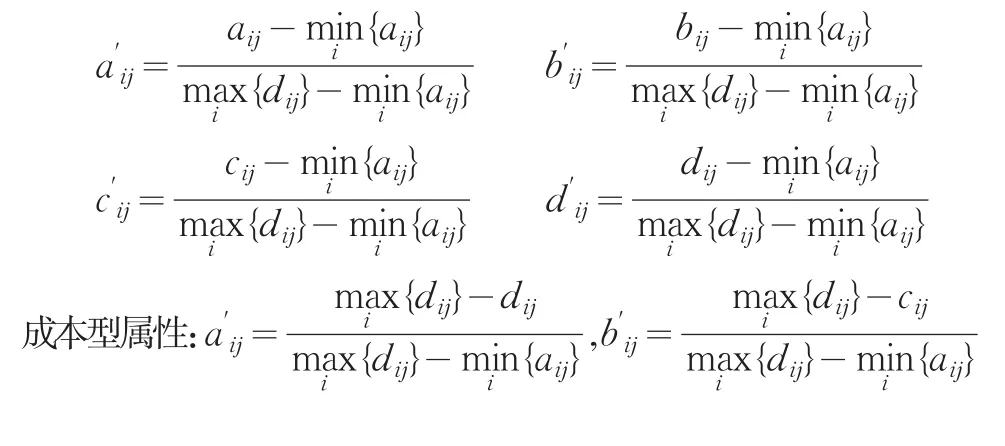
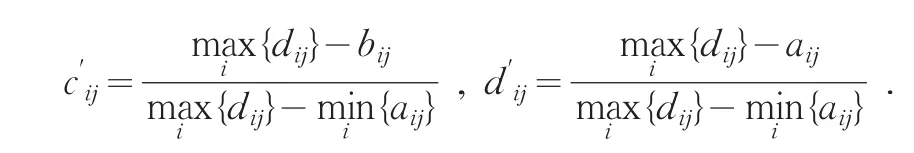
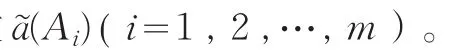
步骤3：根据（2）～（7）式求得各方案Ai的期望值和散度分别为

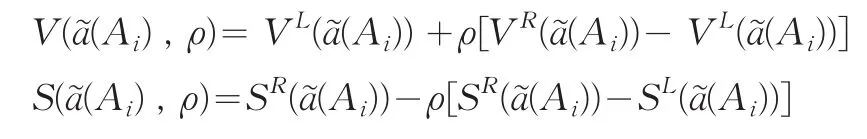
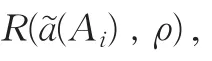
4 实例分析

风险投资是指以未上市公司（尤其是成长型公司或者尚在构思中的公司）为投资对象的一种投资活动.现有某风险投资公司决定对汽车产业,IT信息产业,食品加工产业,文化娱乐产业以及教育培训产业这五大产业领域进行投资,投资总额为1200万元,计划这五个产业领域投资额的比例为4:3:2:2:1.不妨设这五种产业分别记为A1,A2,A3,A4,A5;并且选取5个关键因素作为投资产业的评价指标：市场需求、技术水平、管理质量、环境质量和领域内部竞争力,分别记为C1,C2,C3,C4,C5。这些评价指标均为效益型,投资者根据专家意见和统计数据等确定每个产业领域的评价信息,如表2所示[9]。决策者给出属性权重信息为：

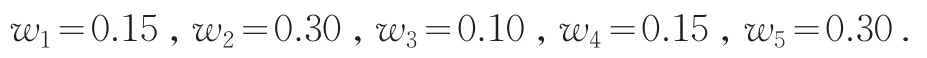
按照本文方法给出具体求解步骤如下。

步骤1：对表1数据进行规范化处理如表3所示。

步骤2：根据（1）式求得各产业Ai的综合直觉梯形模糊数分别为

步骤3：根据（2）～（7）式求得各产业Ai的期望值和散度分别为（取ρ=0.5 ）

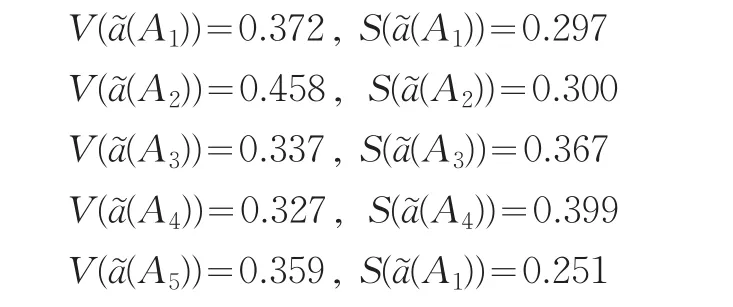
步骤4：根据（8）式求得各产业的优势度指标值为

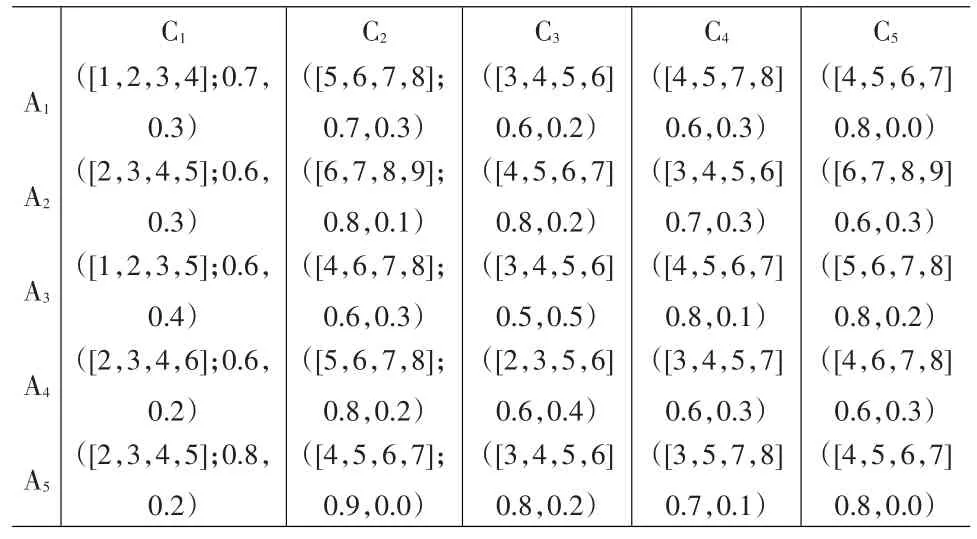
表2 方案的属性值

表3 方案规范化处理后的属性值

从而得到这五个产业领域的排序为A2≻A5≻A1≻A3≻A4。因此按照该公司投资额的比例,这五个产业领域的投资额分别为：IT信息产业400万元,教育培训产业300万元,汽车产业200万元,食品加工产业200万元,文化娱乐产业100万元。

5 结论

由于决策者的偏好会影响排序的结果，本文首先定义了含参数的直觉梯形模糊数的期望值和散度,参数的不同取值代表不同的决策偏好,并综合期望值和散度给出排序直觉梯形模糊数的优势度指标;然后通过具体算例将优势度指标与已有文献中的排序指标进行比较分析,说明优势度排序指标的有效性;最后基于优势度排序指标提出一种直觉梯形模糊数的排序方法，并将其应用到直觉梯形模糊数的多属性决策方法领域。

[1]Atanassov K.Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,1986,20(1).

[2]Atanassov K.More on Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,1989,（33）.

[3]Atanassov K,Gargov G.Interval-valued Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,1989,31(3).

[4]Li D F.Multiattribute Decision Making Models and Methods Using Intuitionistic Fuzzy Sets[J].J.of Computer System Science,2005,70(1).

[5]徐泽水.区间直觉模糊信息的集成方法及其在决策中的应用[J].控制与决策,2007,22(2).

[6]王坚强.信息不完全确定的多准则区间直觉模糊决策方法[J].控制与决策,2006,21(11).

[7]Shu M H,Cheng C H,Chang J R.Using Intuitionistic Fuzzy Sets for Fault-tree on Analysis Printed Circuit Board Assembly[J].Microelectronics Reliability,2006,46(12).

[8]王坚强.模糊多准则决策方法研究综述[J].控制与决策,2008,23(6).

[9]王坚强,张忠.基于直觉模糊数的信息不完全确定的多准则规划方法[J].控制与决策,2008,23(10).

[10]王坚强,张忠.基于直觉梯形模糊数的信息不完全确定的多准则决策方法[J].控制与决策，2009,24(2).

[11]Wang Jianqiang,Zhang Zhong.Aggregation Operators on Intuitionistic Trapezoidal Fuzzy Number and Its Application to Multi-criteria Decision Making Problems[J].J.of Systems Engineering and Electronics,2009,20(2).

[12]万树平,董九英.多属性群决策的直觉梯形模糊数法[J].控制与决策,2010,25(5).

[13]Li D F.A Ratio Ranking Method of Triangular Intuitionistic Fuzzy Numbers and Its Application to MADM Problems[J].Computers and Mathematics with Applications,2007，7（3）.

[14]王坚强.几类信息不完全确定的多准则决策方法研究[D].长沙:中南大学，2005.

[15]Delgado M,Vila M A,Voxman W.On a Canonical Representation of Fuzzy Numbers[J].Fuzzy Sets and Systems,1998,（93）.

[16]Abbasbandy S,Amirfakhrian.The Nearest Trapezoidal Form of a Generaliazed Left Right Fuzzy Number[J].International Journal of Approximate Reasoning,2006,（43）.