具有在位势和力常数交错的一维双原子链晶格振动色散关系

向少华, 邓晓鹏, 施振刚, 文 伟

(怀化学院物理与信息工程系,湖南怀化 418008)

具有在位势和力常数交错的一维双原子链晶格振动色散关系

向少华, 邓晓鹏, 施振刚, 文 伟

(怀化学院物理与信息工程系,湖南怀化 418008)

在简谐近似下,求解了具有在位势和力常数交错的一维双原子链晶格振动的运动学方程.分析了在位势和力常数交错对晶格振动链声学支和光学支的影响.发现了在位势的存在使晶格链产生能隙,并且随在位势的增大,晶格振动频谱发生移动;当在一定的条件下,可使该晶格不存在声学模;交错力常数之比也能提升晶格振动频谱,尤其是对光学支的影响更为显著.

一维双原子链; 在位势; 力常数

0 引 言

晶体由大量的原子(或离子)组成的,并且它们按照一定的方式排列,其主要表现是周期性,即长程有序和对称性1我们所说的晶格是晶体中原子排列的具体形式,因此,原子占据晶格的格点,且在格点附近作微小的振动1晶格振动理论不仅可以用来解释固体的热学性质,而且也是固体宏观性质和微观性质的重要理论基础,对晶体的电学性质、光学性质,超导电性、磁性和相变等许多物理性质都有着重要的作用.

晶格振动是晶体中诸原子实在作集体振动,振动的传播表现为晶格中的格波;一般而言,格波不是简谐的,但可以展成为正交归一的简谐平面波的线性迭加.当振动微弱时,格波可近似为简谐波.这时,各格波之间的相互作用可以忽略,这就是格波所具有的独立模式.晶格的周期性及平移对称性使得其独立的运动模式是分立的.因此,我们可以用独立简谐振子的振动来表述其格波对应集合振动的独立模式,这就是声子.它是一种集体激发的振动形式,服从玻色统计分布.它既可以产生,也可以消灭.

在实际晶格中,原子之间不仅存在相互作用势能,而且还存在与近邻原子无关的在位势[1,2].近年来,在位势对晶格振动色散关系的影响引起了人们浓厚的兴趣和热情.例如:2006年田强等人[2]研究了在位势对于一维双原子链晶格振动长声学波的影响,表明:在位势使色散关系声频支在布里渊区中心的振动频率不再为零,并且随在位势的增大而增大1对于原子之间相互作用势不随在位势大小变化的情况下,晶格振动的色散关系的频隙随在位势的增大而变宽.2009年潘雪琴等人[3]研究了具有在位势的一维双原子链晶格振动的低频支长波模振动图像,得到原胞中两种原子运动的振幅不再一致,低频支长波模不再是原胞质心的运动,且两种原子运动的振幅比随在位势的增大而单调增大.然而,同时具有在位势和力常数交错的一维双原子链振动的色散关系问题目前被研究较少.为此,本文将对这一问题展开研究,推导其动力学方程和分析在位势和力常数等参数对晶格振动色散关系的影响.

1 晶格振动的动力学理论

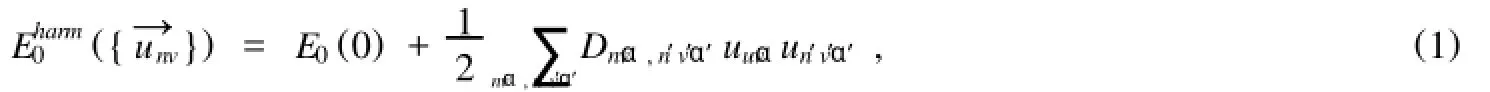
式中,α,α′=x,y,z;v,v′=1,2,…,nb;n=1,2,…,N1在式(1)中不包含位移矢量的线性项,这是因为在平位置附近,静态晶格能对位移矢量的一阶偏导为零,即5E0/ 5unvα=01相邻原子相互作用力常数定义为平衡位置处静态晶格能对位移矢量的二阶偏导,即

由力常数Dnvα,n′v′α′组成的矩阵D应为实数和具有对称性,即

进而可得求和规则

2 一维双原子链晶格振动模型和色散关系

质量分别为m和M,相邻原子之间的平衡距离为a的一维双原子链中,假设最近邻原子间的力常数交错等于κ1和κ21以u2n表示第2n个原子离开平衡位置2na的位移,以u2n+1表示第2n+1个原子离开平衡位置= 2(n+1)a的位移,如图1所示.

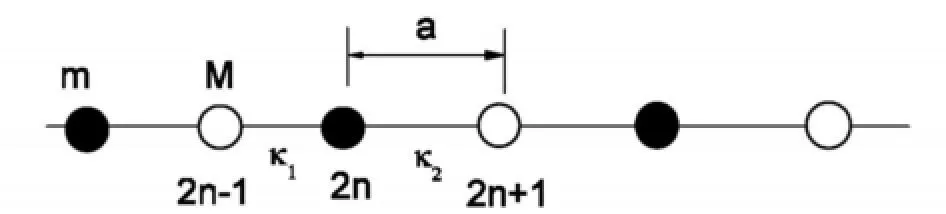
图1 一维双原子链模型

在简谐近似下,具有在位势和力常数交错的一维双原子链晶格振动哈密顿量为

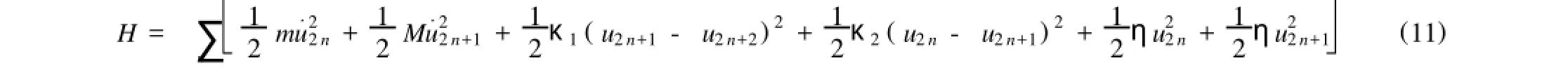
其中η是在位势能的力常数1相应的晶格振动方程为:

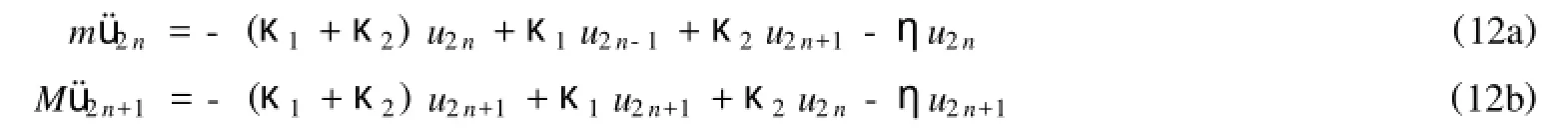
根据第一节的相关知识,线性齐次方程组(12)有行波解:

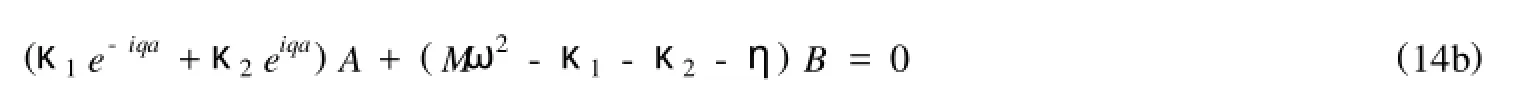
代入运动学方程(12),得到:这是关于A和B的线性齐次方程组1A与B有非零解的条件是系数行列式(9)为零,进而可得晶格振动的色散关系是

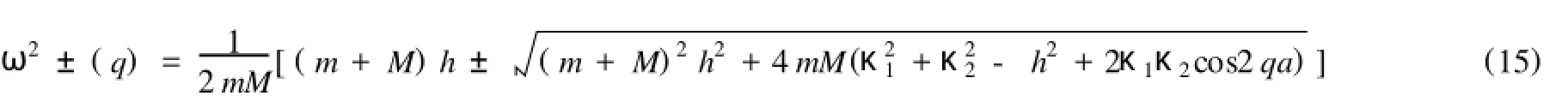
式中h=κ1+κ2+η.由此可以看出,当κ1=κ2,则式(15)回归到文献[3]的色散关系;若两个原子完全等同,则式(15)就是一维单原子链晶格振动的色散关系.另外,根据式(15),不难看出,色散关系有两支,分别称为高频支和低频支;若无在位势,这两支就是固体物理学中提到的光学波和声学波1因此,在位势的存在影响着晶格振动的色散关系,进而影响着晶格的物理特性.下面分多种情况讨论具有在位势和力常数交错的一维双原子链晶格振动的色散关系.

3 一维双原子晶格振动色散关系

在晶格振动色散关系的研究中,通常选取波矢在简约布里渊区,因此下面仅考虑在简约布里渊区的色散关系图,其它布里渊区的情况可通过对称平移而得到1此外,我们在作图的过程中选取两个原子的质量之比是M/m=4和图注的简洁,已假定,这一处理对所获得的结果没有影响1图2中我们考虑不同力常数和在位势对一维双原子链晶格振动色散关系中声学支的影响,并选取参数η / κ1=015,而图3考虑一维双原子链晶格振动色散关系光学支在不同强度力常数和在位势下的变化规律,这里我们已假定κ2/ κ1=21

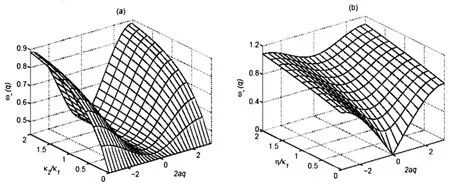
图2 力常数和在位势对一维双原子链声学支的影响

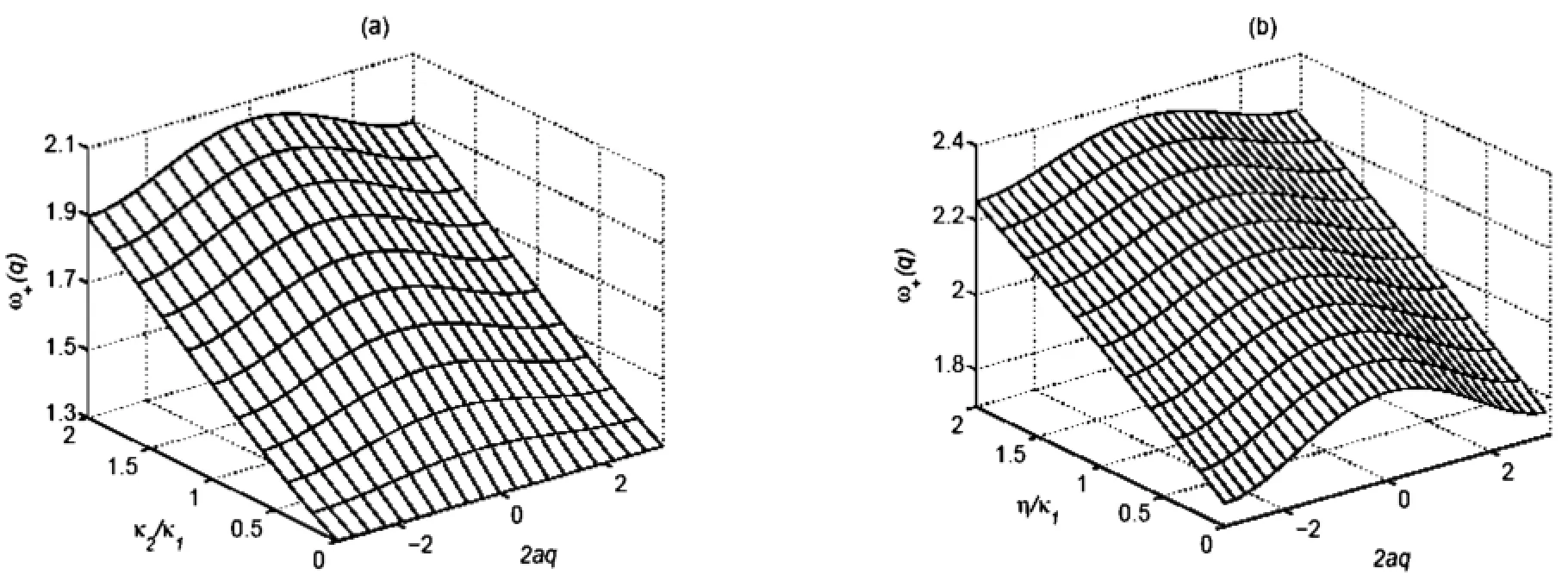
图3 力常数和在位势对一维双原子链光学支的影响

从图2和图3可以看出,两个力常数之比和在位势显著地影响着晶格振动的色散关系,使色散关系ω(q)各处均有不同程度的升高1现在着重考察布里渊区底部和顶部的色散关系,即q=0和q=' /2a的情况1根据式(15),不难得到晶格振动声频支底为

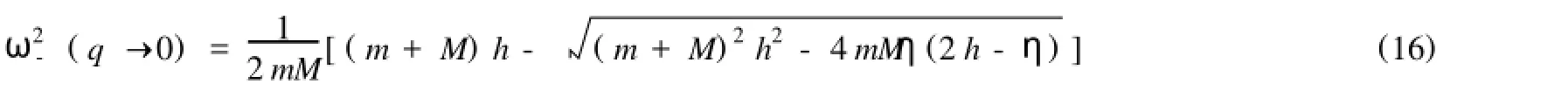
由此可以看出,若晶格中无在位势,无论两个原子的质量和力常数之比如何变化,声学波的长波极限为ω2-(q→0)→0;但当晶格中有在位势时,则ω-(0)≠0,在此出现了频隙,这是有在位势时色散关系的一个显著标志,并且随着在位势和力常数之比的增大而ω-(0)呈非线性增加1对于晶格振动声频支顶有

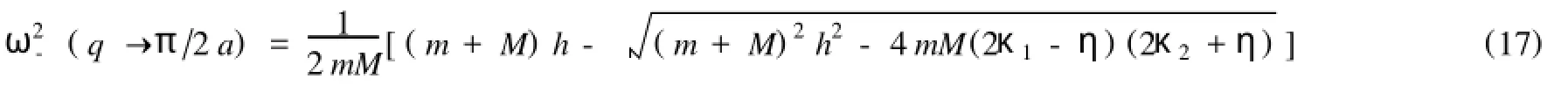
由此可以看出,它不仅与两个原子的质量和力常数之比有关,而且也与在位势有关.当力常数之比(κ2/ κ1)增大时,声频支顶的最大值呈非线性增加,而当κ2=0,κ1→∞,此时晶格振动的色散关系为一条平坦的直线1也即原子链可视为一系列孤立的原子对组成,只有当这些孤立的原子对之间有相互作用时,它们就有可能形成力常数交错的原子链,互相耦合在一起的原子振动便形成了格波.当在位势变化时,声频支顶的最大值随它的增加而呈线性的增加.

对于晶格振动的光学支,我们考察它的布里渊区底和顶.在它的长波极限下,有

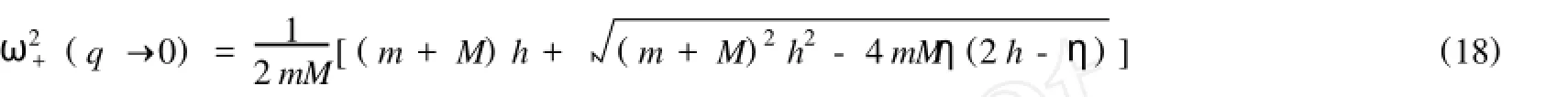
由此可以看出,光频支顶ω+(0)因在位势的存在而显著地升高;而力常数之比对它变化规律影响是:当κ2/ κ1增大时,光频支顶ω+(0)增大,反之,κ2/ κ1趋近于零,ω+(0)将趋近于一常数.在布里渊区的边界(q=2' /a),格波频率为

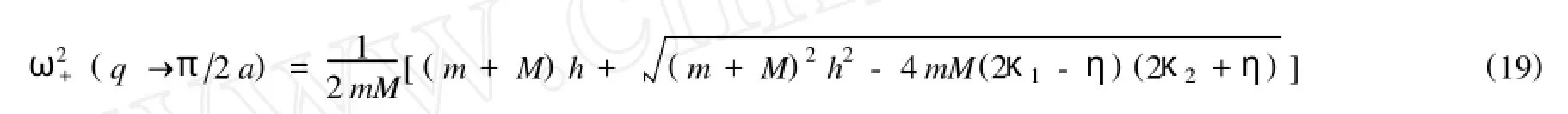
这表明在位势的存在使晶格振动频隙变宽,同时,由图3也不难看出,对于光学支,其最大值与最小值随力常数之比和在位势的增加而呈线性的变化.

最后,我们考察整个简约布里渊区的色散关系.不难发现,在位势的存在时,晶格振动的色散关系跟布里渊区底与顶的变化规律相同,即,力常数之比使声学模频率呈非线性地增加,而在位势使声学支最小值呈线性增加,最大值呈线性变化;而对于光学支,它们使光学支频率的最值呈线性变化.

4 结 论

在《固体物理学》原子晶格振动的教学中,我们一般不考虑在位势对晶格振动色散关系的影响,然而当原子链处于一定的介质环境中,原子链不仅存在原子之间的相互作用势能,还具有与邻近原子无关的在位势1另外,由于原子点阵的不同,原子之间耦合强度也不同1本文研究了简谐近似下,力常数交错和具有在位势的一维双原子链晶格振动运动方程,得到并分析了在位势和力常数交错等因素对晶格振动色散关系的影响1发现:(1)具有在位势的一维双原子链的晶格振动色散关系,在q→0时出现了能隙,这个能隙随着在位势强度的增大而增大; (2)原子之间相互作用势的变化,不会对q→0处的能隙产生影响,但当存在在位势时,却能显著地影响晶格振动的色散关系.

[1]G orbach A V,Johansson M.Discrete gap breathers in a diatomic K lein-G ordon chain:stability and mocility[J].Phys Rev E,2003, 67:066 608.

[2]田强,洪馥男.具有在位势的一维双原子链晶格振动的色散关系[J].大学物理,2006,25(4):17-19.

[3]潘学琴,刘炳灿,田强.在位势对于一维双原子链晶格振动长声学波的影响[J].大学物理,2009,28(5):11-13.

Abstract:Using the harmonic approximation method,the motion equation of one-dimension diatomic chain with on-site potential and force constant cross is solved and the influences of on-site potential andforce constant cross on its dispersion relation are discussed.It has showed that the on-site potential induces the energy gap of one-dimension diatomic chain.When on-site potential increases,the lattice vibration spectra are shifted.No acoustic branches are allowed in the one-dimension diatomic chain under given conditions.The force constant cross is contributed to the shift of the lattice vibration spectra,especially for optical branches.

Key words:one-dimension diatomic chain; on-site potential; force constant crosses

Dispersion Relations of One-dimension Diatomic Chain with On-site Potential and Force Constant Crosses

XIANG Shao-hua, DENG Xiao-peng, SHI Zhen-gang, WEN Wei
(Department of Physics and Information Engineering,Huaihua University,Huaihua,Hunan 418008)

O472

A

1671-9743(2011)02-0033-04

2011-01-11

向少华(1972-),男,湖南麻阳人,怀化学院副教授,博士,主要研究量子信息和物理教学1