一种不确定性机器人的变结构控制

周景雷

(菏泽学院机电工程系,山东菏泽 274015)

一种不确定性机器人的变结构控制

周景雷

(菏泽学院机电工程系,山东菏泽 274015)

考虑机器人的不确定项,首先利用反馈控制技术,把基于拉格朗日方程的多关节机器人动力学模型转化成一线性状态方程1然后基于此状态方程,运用变结构控制思想,并结合李雅普诺夫函数设计出一种新的机器人鲁棒控制器,这种控制器能够保证机器人机械臂的跟踪误差渐近收敛到零点.无论是理论推导还是实验仿真都说明了所设计的控制器有着很好的鲁棒性和有效性.

机器人; 不确定性; 变结构控制; 李雅普诺夫函数

1 引 言

变结构控制是由前苏联学者Emelyanov在上世纪50年代提出的一种具有很强鲁棒性的控制策略,后经Utkin[1]和Itkis等人进一步发展研究而日趋成熟1这种控制策略与常规控制的根本区别在于控制的不连续性,即一种使系统“结构”随时间变化的开关特性1该控制特性可以迫使系统在一定特性下沿规定的状态轨迹作小幅度、高频率的上下运动,即所谓的“滑动模态”或“滑模”运动1这种滑动模态是可以设计的,且与系统的参数及扰动无关1这样,处于滑模运动的系统就具有很好的鲁棒性.

由于它对模型的要求比较低,对外界扰动及参数的不确定性具有良好的鲁棒性,所以近年来,变结构控制思想被广泛应用于工程领域,机器人控制系统就是一个很热门的领域1马赛[2]将变结构和观测器结合起来保证了机器人跟踪轨迹的指数收敛;华森[3]考虑了机器人控制系统的死区这一特殊非线性;吴勃[4]和张文辉[5]利用了神经网络控制,他们也都取得了不错的成绩.但是,观测器和神经网络的利用虽然能够给机器人控制系统的稳定带来一些积极因素,但是也势必增加理论和实际控制器设计的困难1所以,我们设计出了一种简单的一般性的变结构控制器,该控制器不但简单易于设计,就稳定性问题也很好地得到了满足.

2 变结构控制的基本原理[6-7]

变结构控制的基本问题如下1设有一控制系统

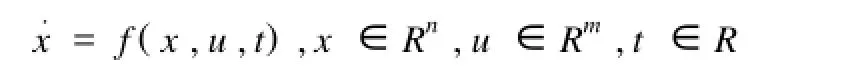
我们需要确定切换函数向量

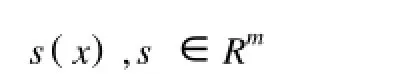
其具有的维数一般等于控制的维数,并且寻求变结构控制

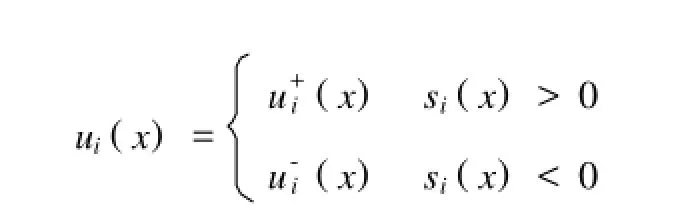
这里变结构体现在u+(x)≠u-(x),使得:切换面si(x)=0以外的相轨迹于有限时间内进入切换面;切换面是滑动模态区;滑动运动渐近稳定,动态品质良好1事实上这些都容易满足,关键是要保证滑动模态的存在,其存在的条件就是

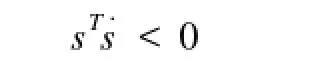
3 机器人系统描述

基于拉格朗日方程的n关节机器人动力学模型在文献[8-9]中多有研究,其可由下面二阶非线性向量微分方程来描述

式中,M(q)∈Rn×n为机器人的惯性矩阵;q,?q,¨q∈Rn为关节位移、速度和加速度;h(q,?q)为离心力、哥氏力及重力的耦合向量;τ为广义关节力矩向量;f为外界不确定项,包含外界干扰和建模误差等1该机器人模型有如下性质(有界性):M(q)为对称正定矩阵,且对于所有的q都是有界的,即存在正数λmΦλM满足不等式λmΦ‖M(q)‖ΦλM1我们通常希望不确定性是有界的,所以要假设f有界.

假设 对于不确定项f,其每一个元素都是有界的,即存在一正向量ρ满足

对于方程(1),我们选择如下广义控制力矩

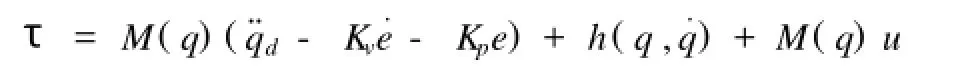
这里,Kv,Kp为正定增益阵,分别可视为微分和比例增益,为了简便,我们在文章中设它们都为对角阵;e=q -qd为关节位移误差,qd为关节期望位移,它们都是二阶可导的;u为外界所加的反馈控制输入,下面就是设计u使得机器人系统满足渐近稳定性目的.

将广义控制力矩带入方程(1),通过化简可得

根据M(q)的性质和对不确定项f所做的假设,我们很容易得出d是有界的,即存在一正向量d0满足下列不等式

4 控制器设计

显然上一小节式(3)中的矩阵A是一正定矩阵[10],于是总存在一个正定解矩阵P对于任一正定矩阵Q满足

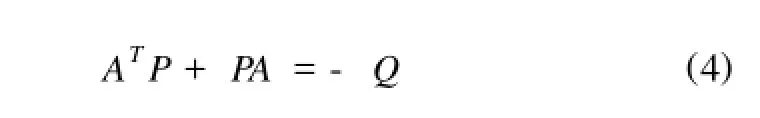
为了下面的需要,在这里我们要定义一个辅助变量^x和一个切换函数向量S,它们分别为

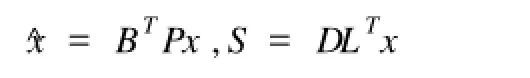
这里P就是式(4)的解矩阵,并且根据正定矩阵的分解我们总可以将其分解为P=LDDLT,L为一下三角矩阵、D为一对角阵,并且它们也都为正定矩阵.

定理 对于系统(3),当选择如下控制律u时,对所有满足假设的不确定项,我们称系统(3)是渐近稳定的.

5 实验仿真

最后我们以两关节机器人机械臂为例来说明我们所设计控制器的有效性和鲁棒性,其中的参数选择和仿真图形见文献[11],限于篇幅在这里我们只给出仿真图形,见下图.图中,e表示跟踪误差,de表示误差的导数,左图表示关节1的误差曲线,右图表示关节2的误差曲线1从仿真图可以看出经过很短的时间,就使得跟踪误差及其导数趋向于零了.

6 结 论

本文依据变结构控制思想,结合控制论中常用的李雅普诺夫函数,设计出了一种机器人机械臂的控制器,该控制器理论简单易于设计,无论从理论方面还是实验方面都证明了文中所设计的控制器是可行的、有效的.

[1]UTKIN V I.Control systems of variable structure[M].New Y ork:Wiley,1976.

[2]马赛,小圣鸿.机器人控制中的变结构观测器[J].舰船电子工程,2009,29(2):158-162.

[3]华森,张天平,朱秋琴,等.带有未知死区的机器人自适应滑模控制[J].中南大学学报,2009,40(S1):102 -107.

[4]吴勃,许文芳,陈虹丽.神经滑模控制在机器人轨迹跟踪中的应用[J].电机与控制学报,2009,13(S1):99 -104.

[5]张文辉,齐乃明,尹洪亮.不确定机器人的神经网络轨迹控制[J].自动化与仪表,2010,(5):22-25.

[6]高为炳.变结构控制基础[M].北京:科学出版社, 1989.

[7]姚琼荟,黄继起,吴汉松.变结构控制系统[M].重庆:重庆大学出版社,1997.

[8]SPONG M W,VIDYSAG AR M.Robot dynamics and control [M].New Y ork:,wiley,1993.

[9]LEWIS F L,ABDALLAH,DAWSON D M.Control of robot manipulators[M].New Y ork:Macmillan,1993.

[10]周景雷,张维海.一种机器人轨迹的鲁棒跟踪控制[J].控制工程,2007,14(3):336-339.

[11]ZHOU J L,ZHANG W H.Robust control for robot with friction based on linear state equation.Proceedings of the 6th International Conference on Intelligent Systems Design and Applications,2006,vol(2):243-248.

Abstract:Considering uncertainties for robot,first,the multi-joint robot dynamics model based on the Lagrange equation is transformed into a linear state equation via feedback control technique.And then,corresponding to the linear state equation,by making use of the variable structure control and the Lyapunov function,an new controller is designed.This controller ensure the robotic tracking errors convergent to be zero.All the theoretical derivation and the simulation results show the robustness and effectiveness of the proposed controller.

Key words:robot; uncertain; variable structure control; Lyapunov function

Variable Structure Control for Uncertain Robot

ZHOU Jing-lei

(Department of Machine and Electronic,Heze,Shandong 274015)

TP24

A

1671-9743(2011)02-0057-03

2011-02-12

山东省自然科学基金(ZR2009GZ001).

周景雷(1981-),男,山东曹县人,菏泽学院教师,硕士,主要研究机器人控制,鲁棒H ∞控制等.