关于一类连续型随机变量的最优区间问题
2011-09-25程财生
苏 强, 程财生
(1.连云港师范高等专科学校,江苏连云港 222006; 2.防化指挥工程学院数学教研室,北京 102205)
关于一类连续型随机变量的最优区间问题
苏 强1, 程财生2
(1.连云港师范高等专科学校,江苏连云港 222006; 2.防化指挥工程学院数学教研室,北京 102205)
设随机变量的概率密度函数为R(Rn)上连续函数,给出最优区间(区域)的概念,讨论最优区间(区域)的必要条件,并且以四个实例说明最优区间的求解思路.
连续型随机变量; 最优区间; 最优区域; 概率密度函数
1 引言和结果
在讲授概率论这门课程时,我们经常会遇到许多具有相同概率的事件,特别是在同一随机变量的情况下,实数集R的不同可测子集所对应事件的概率有时是相同的[1]1后者引起了我们的兴趣,这促使我们提出了一个关于给定概率的最优可测集的问题,即:设连续型随机变量ξ,对于任意给定α(0< α<1),考虑所有概率等于α的事件A,问在什么条件下,数集ξ-1(A)测度最小以及如何找出测度最小的ξ-1(A)?简言之,寻找最小测度的数集,使其对应事件的概率为预先给定值?对于一般的随机变量来说,这个问题比较复杂1在本文中我们就一类简单的情形给出上述问题的一个解答1
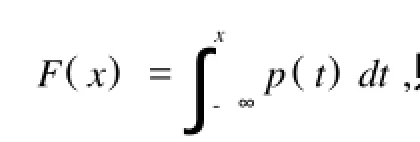
下面定义连续型随机变量的最优区间概念:
定义2 设ξ是一连续型随机变量,对于任意给定的α(0<α<1),如果存在区间[c,d]为使等式成立的长度最小的区间,则称[c,d]为最优区间1

根据定义1,等式(3)可表示为F(d)-F(c)= α 1又知连续型随机变量的分布函数F(x)具有三个基本性质:①F(x)是实数集R上的连续函数;②F(x)是单调不减的;③=11因此满足等式(3)的区间存在,并有无穷多个1
关于最优区间的存在性,本文中不作详细分析1下面给出一类连续型随机变量关于某个给定概率的最优区间问题的一个必要条件:
定理1 设ξ是一连续型随机变量,概率密度函数为p(x),x∈(-∞,+∞)1如果p(x)是一连续函数,对于任意给定的α(0<α<1),使得[a,b]为最优区间的必要条件为p(a)=p(b)1
2 定理1的证明与应用举例
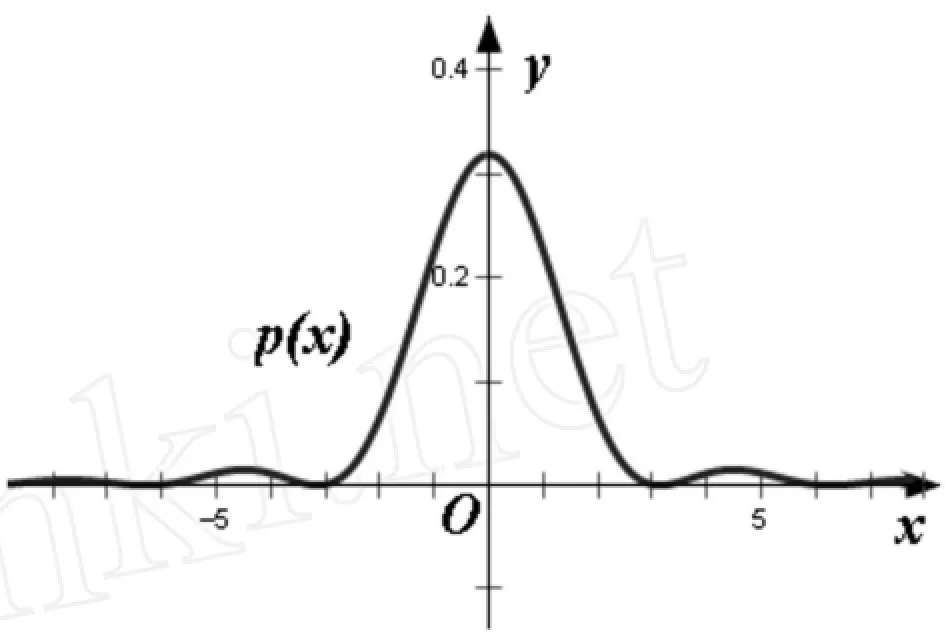
证明:采用反证法1假设p(a)≠p(b)1不妨设p(a) 从而P(x)-P(a)>01这样,就能缩短区间[x, x+b-a]的长度,因而比[a,b]的长度小,这与[a, b]的长度最小相互矛盾1所以p(a)=p(b)1 定理1给我们提供了一个比较有效的办法去寻找给定概率的最优区间,下面结合实例来分析. 例1 设随机变量ξ~N(a,σ2),解释其最优区间情况. 解:对于正态分布ξ,知其概率密度是关于x=a对称的,结合上面的定理,我们知道其最优区间是关于x=Eξ=a对称的,并且最优区间是惟一的1根据标准正态分布表,容易求出给定概率的最优区间. 例2 设随机变量η~p(x),其中 给定概率后,可知其最优区间关于x=0对称,观察概率密度函数p(x)的图像[2](见图1),容易推出最优区间也是惟一的1但p(x)的原函数不能用初等函数表出,所以不能具体写出最优区间. 图1 注:(1)在上面两个例子中最优区间是惟一的,而有时最优区间未必惟一; (2)在实际问题中,可能为最优区间的区间个数仅有有限个,只需在他们之间做简单分析就能找出所求的最优区间1因此,对于满足定理1条件的随机变量,我们都能通过必要条件找出给定概率的最优区间,再做一些比较,就能找出最优区间; (3)一些常用的连续型随机变量其最优区间是比较容易求得,如指数分布ξ~exp(λ)1 下面给出上述理论在高维的推广. 定义3 设η是一n维连续型随机变量,对任意给定的α(0<α<1),如果存在一区域D为使得式P{ω∈Ω|η(ω)∈D}=α成立的长度最小的区间,则称区域D为最优区域. 定理2 设η是多元连续型随机变量,概率密度函数为p(x1,x2,…,xn),其中(x1,x2,…xn)∈Rn,如果p(x1,x2,…,xn)是Rn上连续函数,对于任意给定的α(0<α<1),使得闭区域D为最优区域的必要条件为p(a)=p(b),其中a,b∈5D. 证明 采用反证法1假设存在两点a,b∈5D,使得p(a)≠p(b)1可不妨设p(a) 这样,就能找到更小的区域,从而导致矛盾.因此定理证毕. 注:(4)从几何的角度看,定理2的最优区域D的边界5D是概率密度函数p(x1,x2,…,xn)的等高线[3](或等高面); (5)相对于一维连续型随机变量,多维连续型随机变量的最优区域更复杂些. 例3 设二维随机变量(ξ,η)~p(x,y),其中 解:联合密度函数p(x,y)是平面上连续函数,由定理2可知,最优区域是以原点为中心的圆盘. 对于给定的α(0<α<1),设所对应的圆盘Da的半径为t,则有 [1]李贤平.概率论[Z].北京:高等教育出版社,1998. [2]王昆扬.简明数学分析[Z].北京:高等教育出版社, 2001. [3]威廉·费勒.概率论及其应用(第三版)[M],北京:人民邮电出版社,2006. [4]Г.М.菲赫金哥尔茨.微积分学教程(第八版)第一卷[Z].北京:高等教育出版社,2006. Abstract:This paper discusses a necessary condition for the optimal interval(optimal region)of certain continuous random variable with a given probability and illustrates the solving approaches of the optimal interval via four examples. Key words:continuous random variables; optimal interval; optimal region; probability density function On the Optimal Interval of Certain Continuous Random Variables SU Qiang1, CHENG Cai-sheng2 (1.Lianyungang Teachers'College,Lianyungang,Jiangsu 222006; O211.5 A 1671-9743(2011)02-0030-03 2010-01-20 苏 强(1976-),男,江苏赣榆人,连云港师范高等专科学校讲师,硕士研究生,主要研究高等数学与应用数学; 程财生(1978-),男,江西九江人,北京防化指挥工程学院讲师,硕士研究生,主要研究基础数学1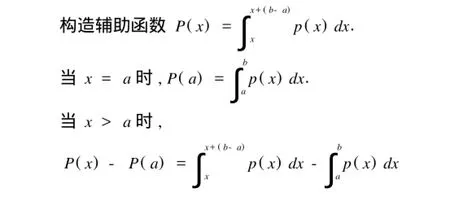


3 定理1的推广与应用


2.Institute of Chemical Defense,Beijing 102205)
