一种实用的GPS坐标及高程同步转换方法*

张兴福 沈云中

(1)广东工业大学测绘工程系，广州510006) 2)同济大学测量与国土信息工程系，上海200092

一种实用的GPS坐标及高程同步转换方法*

张兴福1)沈云中2)

(
1)广东工业大学测绘工程系，广州510006) 2)同济大学测量与国土信息工程系，上海200092

基于GPS控制网三维约束平差基本原理，提出一种GPS坐标及高程同步转换方法，即先由GPS点的空间直角坐标反算点间基线向量，再将旋转参数、尺度参数以及国家坐标系中的坐标作为待估参数，通过附加公共点约束进行坐标及高程转换。利用工程实例数据对该方法进行了试验，结果表明:该方法非常灵活、有效，其坐标及高程转换精度良好。

GPS基线反算;三维约束平差;坐标转换;高程转换;精度分析

AbstractThe synchronous transformation method of GPS coordinate and height based on GPS control network three-dimension constraint adjustment theory is given out.The steps of the method are as follows.At first，the baseline vector between two points is calculated from the three-dimension rectangular coordinate of GPS points，and the rotation parameters，scale parameter and the coordinate parameters in state coordinate system are also regarded as the unknown parameters，the coordinate and height transformation of GPS points are completed through the common points constraint.Finally，a case of GPS control network is used to test the method.The results show that the method is flexible，effective，and the transformation accuracy of coordinate and height are also well.

Key words:GPS baseline calculation;three－dimension constraint adjustment;coordinate transformation;height transformation;accuracy analysis

1 引言

GPS测量技术已经广泛应用到日常测绘工作中，极大地提高了测量工作效率。虽然我国已经建立了高精度的三维地心坐标系——2000国家大地坐标系(CGCS2000)，但很多工程项目还涉及GPS测量成果与1980西安坐标系、1954北京坐标系以及独立坐标系的转换。坐标转换一般可分为坐标系转换和坐标基准转换［1－4］。另外由于GPS测量获得的高程为大地高，而实际工程更需要点的正常高信息，常规的方法是GPS坐标与高程分别进行转换，因此如何在保证一定转换精度的前提下实现GPS坐标及高程的同步转换将具有重要的现实意义。

我国国家平面控制网和高程控制网是分开布设的，有些控制点平面坐标精度很高，而大地高精度较低，甚至根本就没有大地高数据;而有些控制点只有很高精度的正常高，而无大地高及平面坐标。而要完成三维坐标基准转换，就必须知道至少3个公共点的空间直角坐标，这就意味着同一个点的平面坐标和大地高都要已知，且具有足够的精度，这在我国可能较难实现。在这种情况下，很难用常规的空间七参数法实现坐标基准转换。另外基于点坐标的常规空间七参数坐标转换方法也存在一些不足:1)在小区域范围内，旋转参数以及尺度参数和平移参数是强相关的，但旋转参数和尺度参数是不相关的［5］;2)未将点在某一坐标系中的坐标作为待估参数与坐标转换参数一起进行严密平差;3)公共点的误差无法有效地分配到其它待求点;4)公共点的大地高精度低，甚至根本就没有大地高。

针对上述情况，本文基于GPS网的三维约束平差原理，利用已知GPS点的空间直角坐标反算出各点间基线向量，并组成一定的闭合图形，通过附加公共点约束实现坐标及高程转换。该方法属严密平差方法，误差方程式是基于坐标差转换模型，刚好能消除平移参数，避免参数强相关对坐标转换的影响。另外可综合平面坐标(或大地经纬度)与高程(平面坐标和高程可不是同一个点，大地高用正常高代替)，在实现三维空间七参数法坐标转换的同时，将GPS大地高转换为正常高(高程约束点要等于或大于2个)，避免平面坐标与高程不匹配对坐标转换的影响，又可对点在国家坐标或独立坐标系中的坐标进行估计，公共点的误差会通过基线传递到待求点。最后利用某一GPS工程数据对本文方法进行了实验研究，效果良好。

2 原理与方法

GPS控制网的三维约束平差的基本原理是将GPS基线向量作为直接观测量，将控制点在国家或地方独立坐标系中的空间直角坐标作为未知参数，同时考虑GPS测量获得的WGS-84坐标和国家坐标或地方独立坐标的转换关系，通过附加地面控制点约束的方法，将GPS测量成果直接转换为国家坐标系或地方独立坐标系［2］。本文利用GPS点已知的WGS-84坐标反算相邻点间基线向量，借助GPS控制网的三维约束平差原理进行坐标基准转换及高程转换。图1中A、B、C、1、2、3和4为7个GPS点，其中A、B、C为GPS和地面控制点的公共点，1、2、3、4为GPS点，基于三维约束平差理论的GPS坐标转换方法的具体实现过程为:先由7个点WGS-84坐标反算1－2，1－A，A－B等基线组成如图1所示的基线网，然后通过固定A，B，C 3点地面坐标进行三维约束平差即可将其他4个GPS点坐标转换到国家或独立坐标系。

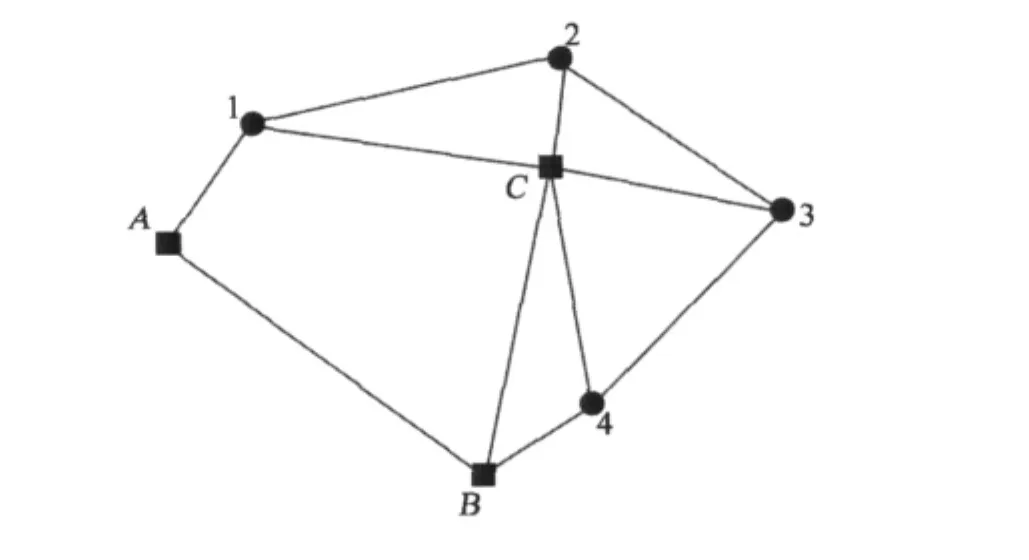
图1 GPS点反算基线Fig.1Baseline network inversed from GPS points

若设i、j为国家或独立坐标系中的两点，其空间直角坐标分别为(XiYiZi)和(XjYjZj)，相应的坐标差为(ΔXijΔYijΔZij)，两点对应WGS-84坐标系坐标差为(Δ¯XijΔ¯YijΔ¯Zij)，现通过坐标差形式计算两坐标系转换参数(3个旋转参数，1个尺度参数)，同时将国家或独立坐标系的空间直角坐标作为未知参数一起求解，则误差方程式为

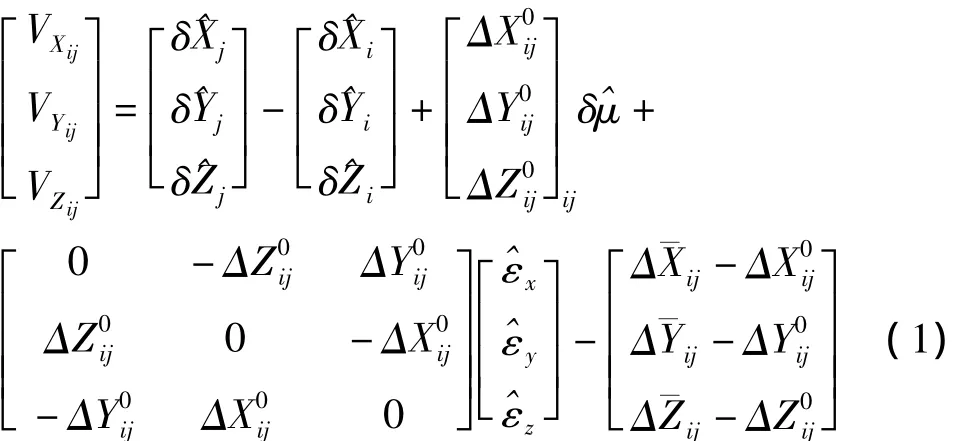
其中，δ^Xi、δ^Yi、δ^Zi、δ^Xj、δ^Yj、δ^Zj为国家坐标系下i、j点的空间坐标改正数，^εx、^εy、^εz为两坐标系旋转参数，且为微小量，δ^μ为尺度参数，上标“0”表示变量的近似值。

若将点的站心地平坐标系作为过渡坐标系［6］，取与局部椭球的定位定向有联系的绕地平北、东方向和天顶方向的旋转角^εη、^εξ和^εA为旋转参数，这3个旋转参数中前两个旋转参数用于实现椭球变换，第三个旋转参数用于坐标方位旋转，则公式(1)可改写为，

（5）菌苗基础研究较为落后。从目前的具体实际分析，菌苗生产和使用的菌种都是20世纪60～70年代分离的菌株，由于时间过长，在免疫特性方面与现代流行性的菌株存在一定的差距，会在一定程度上造成免疫失败。

空间直角坐标系和站心地平坐标系的旋转矩阵，B0和L0为大地经纬度近似值，其他参数含义同公式(1)。

若只考虑将WGS-84坐标系的三维空间直角坐标转换为国家坐标系或独立坐标系中的两维坐标，则式(2)中的基准转换参数可只取尺度参数δμ和绕天顶方向的旋转角εA。

利用式(2)列立坐标基准转换误差方程式后，其法方程秩亏，无法解算转换参数及待求的国家或独立坐标系中的未知坐标参数，因此需附加基准条件，若K点在国家或独立坐标系中的大地纬度、大地经度和大地高已知，则可列立约束条件，

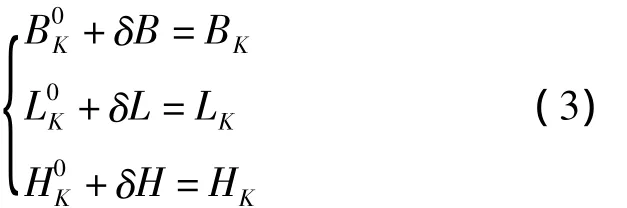
其中，BK、LK、HK为已知值，B0K、L0K、H0K为概略值，而δB、δL、δH为改正数，若取B0K=BK，L0K=LK，H0K=HK，则δB=δL=δH=0。

由于将空间直角坐标作为待求参数，为了建立大地经纬度改正数以及大地高改正数与空间直角坐标改正数的关系式，可对大地坐标与空间直角坐标转换公式进行全微分，整理可得，其中，P为WGS-84坐标系中的基线向量权矩阵，若GPS点坐标方差已知则可计算相应基线的权阵，若GPS点方差未知则可用单位阵代替，而K为联系系数，利用式(5)即可以将GPS测量获得的WGS－84坐标转换为国家或独立坐标系。实际计算中，若公共点的平面坐标已知，则可以用公式(3)、(4)中的前两项列立条件方程，若公共点的高程已知，则可用公式(3)、(4)中的最后一项列立条件方程。该方法可通过综合公共点的平面坐标和高程信息实现GPS坐标转换及高程转换。

3 算例与精度分析

选择某一城市GPS控制网数据作为算例，该控制网控制范围约1 000 km2，平均点间距约4 km，从控制网中选择42个点，其中含已知平面点5个，坐标基准为1980西安坐标系，34个GPS点联测了正常高，高程基准为1985国家高程基准。坐标基准转换过程为:

1)利用42个GPS点在WGS-84坐标系中的空间直角坐标反算两点间的基线向量，并取各基线向量权阵为单位阵，并组成一定的闭合图形，GPS点的WGS-84坐标为无约束平差结果，组成的GPS基线网的示意图见图2。图中实方框表示平面已知点，实三角形表示三维坐标已知点，实圆点表示三维坐标都未知的点，十字丝表示正常高已知的点。无论是否采用无约束平差坐标，由于基线是由坐标推算出来的，因此组成的闭合图形的闭合差均为零。

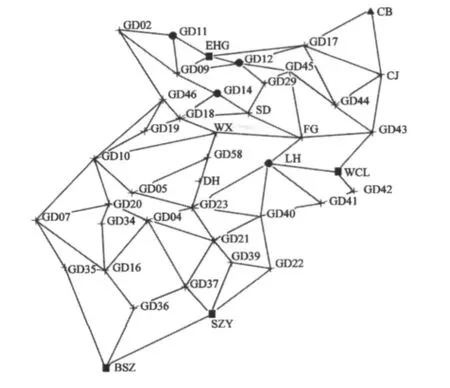
图2 GPS点基线组网Fig.2GPS baseline network

3)采用自编程序进行坐标基准转换，求取两坐标系3个旋转参数(仅考虑平面坐标转换时，旋转参数为一个)，1个尺度参数以及点在国家或独立坐标系中的坐标。此过程需要迭代计算，直到待估坐标参数改正数小于设置的限差为止，国家坐标系或独立坐标系中点的待估坐标的初值可用WGS-84坐标代替，此过程一般只需要迭代3次即可收敛。

3.1 GPS三维坐标转换为平面坐标及精度分析

当将三维的GPS网转换到由常规技术构建的国家或独立坐标系时，实际上这种控制网只是两维网，因此很难获得可靠且相互独立的3个旋转参数，对于地面点仅能固定一个点的三维坐标，其余地面点充其量仅能固定两维坐标(大地经纬度)。现选择CB点的三维坐标(大地经纬度，大地高用正常高代替或取概略值)，BSZ点，WCL点以及EHG点的大地经纬度作为约束条件，利用推算出来的86条基线进行坐标基准转换，由于只固定了一个点的高程，该高程起高程基准作用，因此基准转换参数只取旋转参数εA以及尺度参数δμ，此过程获得的点的高程成果不可用，将其基准转换获得的平面坐标成果称为CASE 1，相应的基线改正数统计结果见表1，旋转参数εA=－0.19 s，δμ=2.65 ppm，而将用原始GPS数据解算得到的基线及方差信息和同样控制点进行约束平差获得平面坐标成果称为CASE 0，现对两者进行比较，结果见图3。

图3和表1结果显示:利用本文方法将GPS网三维坐标转换为国家坐标系的成果与严密平差方法转换的结果相差不大，除3个点坐标的y方向差值超过10mm外，其他点x、y方向差值均不超过10 mm，x、y方向差值的中误差分别为3.3 mm和5.2 mm，说明本文基准转换方法是可靠的。在基准转换过程中基线改正数绝大部分都小于1 cm，最大为2.35 cm，由于推算获得的GPS基线网的闭合差为零，基线改正数应当主要是由点在国家坐标系中的误差分配造成的。

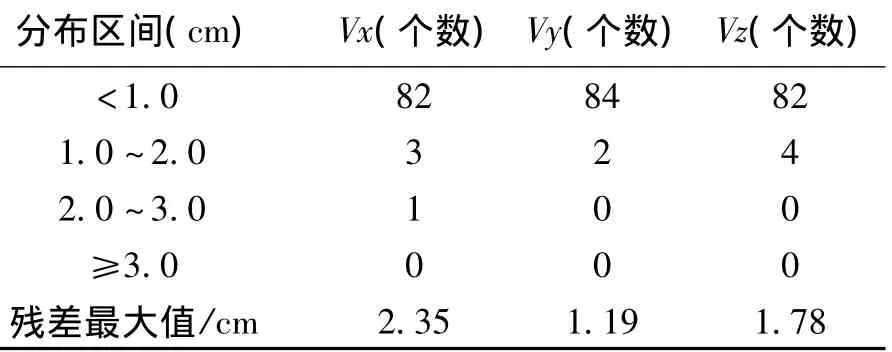
表1 坐标转换基线改正数统计结果(CASE 1)Tab.1Statistic results of corrected baseline value(CASE 1)

图3 CASE 1与CASE 0坐标比较Fig.3Comparison of the coordinates between CASE 1 and CASE 0

3.2 GPS三维坐标同步转换为平面坐标和高程及精度分析

由于我国平面控制和高程控制通常是分开布设的，因此很难获得地面点的真正三维坐标，有些地面点可能只有大地经纬度(平面坐标可反算出大地经纬度)，而无准确的大地高信息;有些点可能只有高程信息，特别是正常高信息，而无大地经纬度。如何综合利用地面点分离的大地经纬度和正常高信息，通过三维坐标转换的方法，实现将GPS测量成果转换为国家坐标系中的平面坐标，同时将GPS大地高转换为正常高，这正是本文研究的内容。本文在将CB点的三维坐标(大地经纬度及正常高)，BSZ点、WCL点以及EHG点大地经纬度作为约束条件外，另将点G02、G58、G07、G37和G41的正常高作约束条件，其平面坐标转换结果称为CASE 2，相应的基线改正数统计结果见表2，与CSAE 1相应的旋转参数，εA=－0.20 s，δμ=2.55 ppm，由于采用三维坐标转换方法，转换参数除εA和δμ外还有和两个转换参数，其与CASE 0坐标转换的比较结果见图4，CASE 2和CASE 1转换坐标比较结果见图5。从两种方法计算获得的对应的旋转参数以及尺度参数可以看出:两者差别非常小，方位旋转参数差了0.01 s，而尺度参数差了0.1 ppm，因此增加高程约束点对方位旋转参数以及尺度参数影响可忽略。

图4、图5和表2结果显示:虽然增加了5个高程约束点，采用3个旋转参数和一个尺度参数实现坐标和高程的同步转换，坐标转换结果和CASE 0结果比较，同样除3个点坐标的y方向差值超过10 mm外，其他点x、y方向差值均不超过10 mm，x、y方向差值的中误差分别为3.6 mm和6.3 mm。将CASE 2和CASE 1结果比较，x、y方向差值的中误差分别为1.6 mm和3.6 mm，在该区域，增加高程点约束对y方向的影响要稍微大于x方向影响，整体看，增加高程约束点对平面坐标转换结果的影响比较小，但对基线改正还是有一定的影响，特别是对y和z方向影响较大。

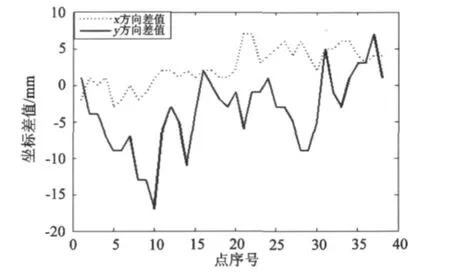
图4 CASE 2与CASE 0坐标比较Fig.4Comparison of the coordinates between CASE 2 and CASE 0

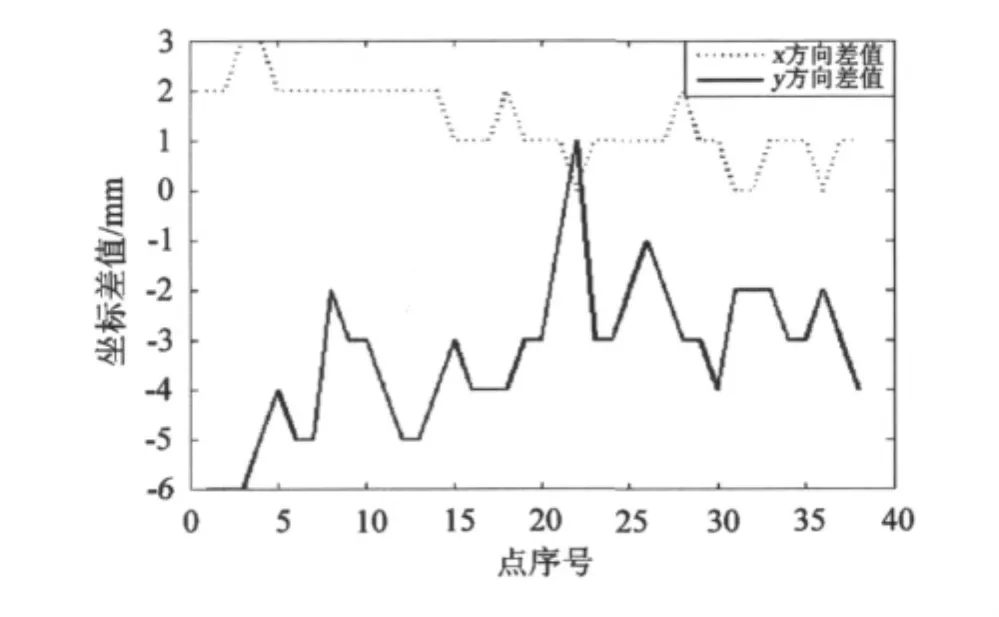
图5 CASE 1与CASE 2坐标比较Fig.5Comparison of the coordinates between CASE 1 and CASE2

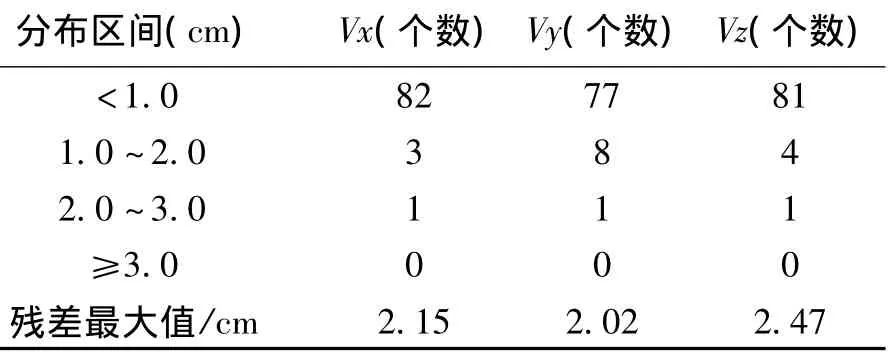
表2 坐标转换基线改正数统计结果(CASE 2)Tab.2Statistic results of corrected baseline values(CASE 2)

当作为高程约束点超过1个时，若将选择的正常高为高程约束量，则通过三维坐标转换方法，在将GPS点三维坐标转换到国家坐标系大地经纬度的同时，也可以将GPS大地高转换为正常高，图6为CSAE 2转换成果中的高程结果与实测水准高程的比较，图6结果显示:其高程转换结果和实测水准高的差值绝对值不超过50 mm，差值中误差为23.8 mm，高程转换的精度非常高。

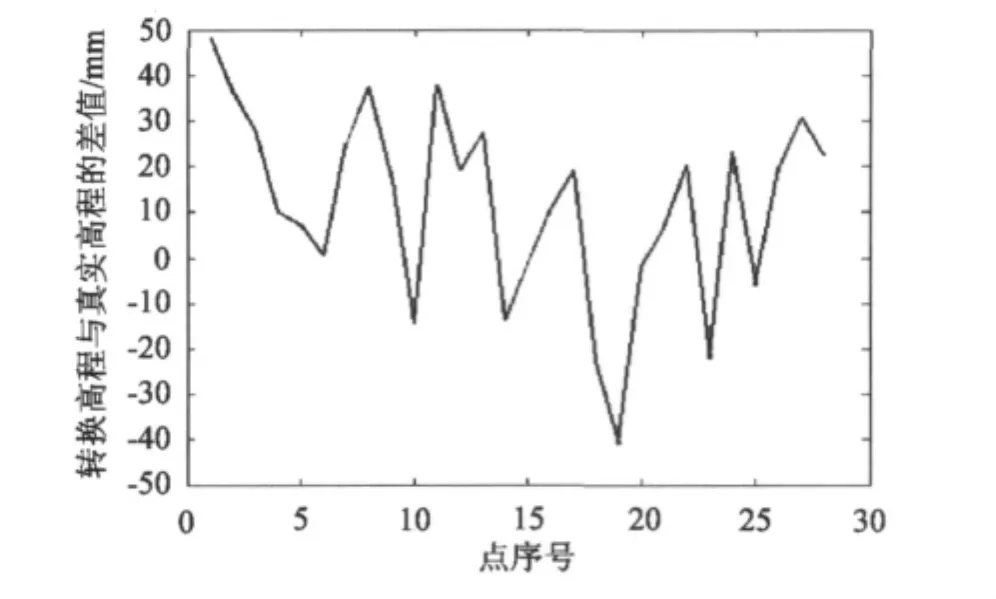
图6 CASE 2高程与真实高程比较Fig.6Comparison of the heights between CASE 2 and true one

4 结论

1)基于GPS三维约束平差理论，推导了顾及旋转参数(3个或一个)、尺度参数以及国家坐标系或独立坐标系坐标参数为待求参数的坐标转换模型，该方法利用GPS点空间直角坐标反算点间基线向量，并通过附加大地经纬度和正常高的方法实现GPS坐标及高程的同步转换，地面约束点无需具有三维坐标，可根据情况分别选择大地经纬度和高程约束点，非常灵活。

2)实际应用中，GPS点的空间直角坐标可以采用无约束平差成果，也可以采用其他方法获得的成果，如GPS-RTK等，对于有点的方差信息，可通过点的方差信息计算对应基线权矩阵;若没有精度信息，可将反算基线权矩阵定为单位权。无论采用那种方法获得的成果，若形成闭合图形，则闭合差均为零。

3)利用常规的空间七参数方法进行坐标转换，旋转参数及尺度参数与平移参数强相关，而本方法能消除这种相关性;另外公共点会有残差，其残差一般很难进行分配，而本方法将公共点作为强制约束点，转换之后不存在残差，那么公共点的误差会通过反算的基线传递到其他待求点，并进行整体分配。

4)GPS坐标及高程的同步转换方法既可将GPS坐标转换为国家坐标系中的平面坐标，又可实现GPS高程转换，其平面坐标转换精度与GPS控制网严密平差方法相差很小，高程转换精度也很高，更重要的是增加高程约束点对平面坐标转换的影响较小。因此本文方法比较适合区域不大且地形起伏相对较小测区的GPS坐标及高程同步转换。

1施一民.现代大地控制测量［M］.上海:同济大学出版社，2003.(Shi Yimin.Modern geodesy control surveying［M］.Shanghai:Tongji University Press，2003)

2刘大杰，等.全球定位系统(GPS)的原理与数据处理［M］.上海:同济大学出版社，1996.(Liu Dajie，et al.The theory and data processing of Global Positioning system［M］.Shanghai:Tongji University Press，1996)

3朱华统，等.GPS坐标系统的变换［M］.北京:测绘出版社，1994.(Zhu Huatong，et al.Transformation of GPS coordinate system［M］.Beijing:Surveying and Mapping Press，1994)

4杨元喜，徐天河.不同坐标系综合变换法［J］.武汉大学学报(信息科学版)，2001，26(6):509－512.(Yang Yuanxi and Xu Tianhe.The combined method of datum transformation between different coordinate systems［J］.Geomatics and Information Science of Wuhan University，2001，26(6):509－512)

5王解先.七参数转换中参数之间的相关性［J］.大地测量与地球动力学，2007，(2):43－46.(Wang Jiexian.Correlations among parameters in seven parameter transformation model［J］.Journal of Geodesy and Geodynamics，2007，(2):43–46)

6沈云中，卫刚.利用过渡坐标系改进3维坐标变换模型［J］.测绘学报，1998，27(2):161－165.(Shen Yunzhong and Wei Gang.Improvement of three dimensional coordinate transformation model by use of interim coordinate system［J］.Acta Geodaetica et Cartographica Sinica，1998，27(2): 161－165 )

A PRACTICAL METHOD FOR SYNCHRONOUS TRANSFORMATION OF GPS COORDINATE AND HEIGHT

Zhang Xingfu1)and Shen Yunzhong2)(
1)Department of Surveying and Mapping，Guangdong University of Technology，Guangzhou510006) 2)Department of Surveying and Geomatics，Tongji University，Shanghai 200092

P226+.3

A

1671-5942(2011)03-0063-06

2010-11-13

中国科学院动力大地测量学重点实验室开放基金(L09－07)

张兴福，男，1977年生，副教授，主要从事卫星重力、GPS数据处理及应用软件开发.E－mail:xfzhang77@163.com