基于提升小波的单历元GPS变形监测信号的去噪*

陶庭 叶高飞 吴兆福

(合肥工业大学土木与水利工程学院，合肥230009)

基于提升小波的单历元GPS变形监测信号的去噪*

陶庭 叶高飞 吴兆福

(合肥工业大学土木与水利工程学院，合肥230009)

介绍提升小波阈值收缩法去噪的基本原理和方法，利用该方法对含噪的GPS单历元变形监测数据进行去噪，提取真实变形信息。实际数据处理结果表明，相比第一代小波，提升小波变换去噪效果更好，计算速度更快。

提升小波;变形监测;GPS;高频噪声;去噪

AbstractThe threshold shrinkage denoising method based on lifting wavelet transform is expatiated.Besides，the method is used to filter the noise from single epoch GPS deformation monitoring data and get the real deformation information.The experimental data processing results show that the advantage of lifting wavelet transform lies on better denoising effect and consuming shorter time than traditional wavelet transform.

Key words:lifting wavelet;deformation monitoring;GPS;high frequency noise;denoising

1 引言

GPS技术在各类变形监测中得到广泛应用。通常，GPS变形观测的作业方式有周期性的重复测量、固定连续GPS测站阵列与实时动态3种［1］。GPS实时动态变形监测采用的是RTK技术，即实时动态载波相位差分GPS测量，其定位方式属于双差相位观测模型，常用于建筑物、桥梁监测。实时动态监测时基准站与监测站距离比较近，属于短基线差分GPS测量，其中大多数误差可以通过差分方法消除或减弱。而单历元变形信息属于高采样频率的数据源，受各种干扰信号的影响，解算得到的变形信息中会有大量高频噪声。因此要获得准确的变形信号必须要对GPS变形坐标序列进行去噪。

文献［2］提出的第二代小波变换是一种基于时域运算的信号分析方法，与第一代小波变换不同的是，它不依赖傅里叶变换，放弃了伸缩和平移条件，却同样可以获得与经典小波变换相同的时频特性，且可通过设计预测系数和提升系数，构造某种特性的第一代小波。提升小波降低了传统的小波变换的计算复杂度，提高了去噪效率，且无需额外内存。

本文利用提升小波对GPS动态变形监测坐标序列数据进行去噪，提取真实的变形信息。试验数据处理结果表明，该方法具有去噪效果好、计算速度快等优点。

2 基于提升小波的阈值去噪

2.1 提升小波

基于提升方案的小波变换称为提升小波变换［3－5］。

设数据序列为λ={λ(k)，k∈Z}，基于提升方案的小波变换可以用以下3个步骤描述［4］:

1)分裂:将数据序列{λ(k)，k∈Z}分为奇样本序列{λodd(k)，k∈Z}(λodd(k)表示奇样本)和偶样本序列{λeven(k)，k∈Z}(λeven(k)为偶样本)。

2)预测:dj(k)=λ(2k+1)－P(λ(2k))，k∈Z。P为预测算子，所得dj为小波系数。

3)更新:cj(k)=λ(2k)－U(dj(k))，k∈Z。U为更新算子，所得cj为尺度系数。

重复以上3个步骤就可以创建多分辨分解的多级变换。图1表示的是提升算法的分解过程与重构过程。

图1 提升小波变换Fig.1Lifting wavelet transformation

2.2 基于提升小波的阈值收缩法去噪

小波阈值收缩法去噪的原理为［6］:由于小波变换具有很强的去数据相关性，小波变换后的信号能量主要集中小波域中在一些大的小波系数中;而噪声的能量却在小波变换后分散到各个小波域。经小波分解后的有用信号的小波系数幅值要明显大于小波分解后噪声的小波系数幅值。因此，可将幅值比较大的小波系数看作是有用信号，而将幅值比较小的小波系数当作噪声。而采用阈值收缩法消噪就是保留用信号的小波系数而减小大部分噪声的小波系数。

提升小波阈值收缩法去噪的基本步骤是:

1)先对含噪信号s做提升小波变换得到一组小波系数wj，k;

2)通过对wj，k进行阈值处理得出估计小波系数w^j，k使得w^j，k－wj，k尽可能小;阈值法分为软阈值法与硬阈值法［6］。

软阈值的算法如下:

该算法将信号分解后的小波系数与依公式所求的阈值λ进行比较，如果某点小波系数大于等于阈值，则该点小波系数收缩变成该点小波系数与阈值的差值;如果某点的小波系数小于阈值相反数，则该点的小波系数收缩为该点的小波系数与阈值的和;如果该点的小波系数的绝对值小于等于阈值，则该点的小波系数变为零。

硬阈值的算法如下:

该算法同样是将信号分解后的小波系数与依公式所求的阈值λ进行比较，如果某点的小波系数的绝对值大于等于阈值，则该点的小波系数保持不变;如果某点的小波系数的绝对值小于阈值，则该点的小波系数变为零。

3)根据收缩得到的小波系数~wj，k，利用提升小波对信号进行重构，得到的信号^s即为去噪之后的信号。

3 基于提升小波的单历元GPS变形监测信号的去噪

3.1 数据来源

试验地点选在某实验楼顶，基准站设在地面稳定的观测墩上固定不动。流动站天线设置在楼顶某细钢筋上。由于风力等其他因素作用，钢筋会发生位移。基准站与流动站周围开阔，没有反射物体，不会产生多路径效应误差。两站之间距离只有100多米，属于短基线差分GPS测量。其中的大多数误差都可以通过差分方法消除或削弱，如卫星钟差、接收机钟差可以完全消除;而卫星轨道误差、对流层延迟误差、电离层延迟误差等能得以很好地削弱。因此，观测所得坐标序列的误差主要为高频噪声。选用Leica GPS1200双频接收机，将采样率设为1 Hz，卫星的截止高度角设为20°。

图2是X方向含噪声的4 000个历元的GPS变形监测数据，从图2中可以看出真实的变形信号受到噪声的污染，要获得准确的变形信息，必须对该信号进行去噪。

3.2 数据处理

分别采用提升小波与传统小波对含噪信号进行阈值收缩法去噪。

首先选用第一代小波，采用阈值收缩法去噪，选用的小波基为具有正交紧支撑的Daubechies小波。选用db2小波，进行阈值收缩法消噪。去噪结果如图3所示。

再利用提升db2小波对上述观测值信号做小波分解及相关的阈值消噪处理。进行4层分解，利用阈值收缩法把分解得到的小波系数进行收缩处理，再利用收缩后的小波系数进行信号重构。图4为提升小波去噪后得到的信号。

通过降噪处理，原始信号中的噪声基本被滤除，得到的有用信息客观地反映了原始信号的主要成分。现在采用去噪后的信噪比与均方根误差来定量地分析两种小波去噪效果。

图2 含噪声的GPS单历元变形监测信号Fig.2Nosing single epoch GPS deformation monitoring signal

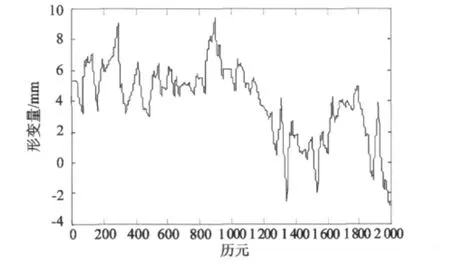
图3 传统小波去噪结果Fig.3Denoising results by using traditional wavelet

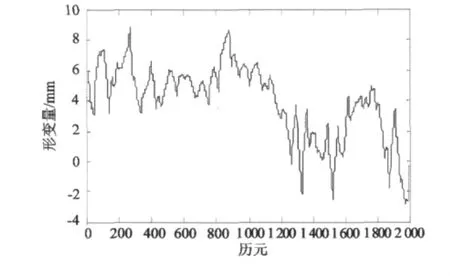
图4 提升小波去噪结果Fig.4Denoising results by using lifting wavlet

信噪比定义为:

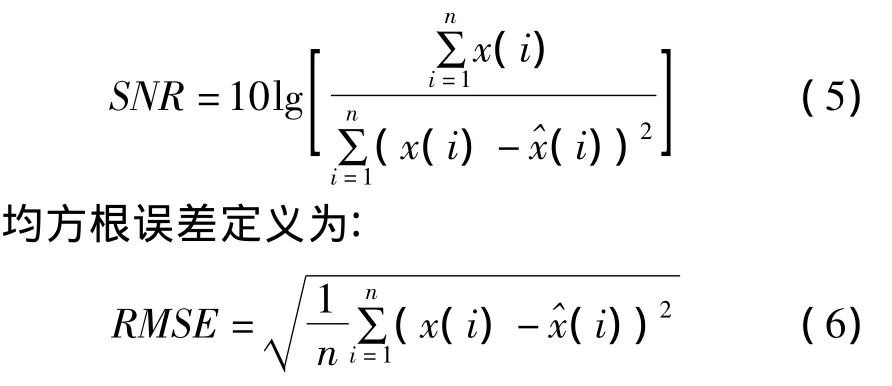
这里，x(i)为标准信号，^x(i))为消噪后得到的估计信号，n为原始信号的长度。

信号的信噪比越高，原始信号与估计信号的均方根误差越小，表明估计信号就越接近于原始信号，去噪效果越好。两种小波去噪后，其信噪比与均方根结果如表1所示。

表1 两种方案去噪效果比较Tab.1Comparison between denoising results with the two different methods

在耗费时间方面，采用第一代小波所需的CPU时间为7.984 4 s，而采用第二代提升小波所耗费的CPU时间为7.515 6 s，说明第二代小波计算速度更快。

上述数据处理结果表明，提升小波及其传统小波均能将含噪的变形信号中的高频噪声滤除，但提升小波滤波后的信号信噪比更大，原始信号与估计信号的均方根误差更小，这说明相比第一代小波，提升小波的降噪效果更好。另外，提升小波的计算速度比传统小波更快。

4 结语

单历元GPS变形监测信号的去噪结果表明:利用提升小波能更好地对单历元GPS变形监测信号进行去噪，有效提取真实变形信息;相比传统小波其计算速度更快，这一点在处理海量数据时优势明显。

1戴吾蛟，等.GPS建筑物振动变形监测中的单历元算法研究［J］.武汉大学学报(信息科学版)，2007，3(4):321－327.(Dai Wujiao，et al.Single epoch ambiguity resolution in structure monitoring using GPS［J］.Geomatics and Information Science of Wuhan University，2007，3(4):321－327)

2孙延奎.小波分析及其应用［M］.北京:机械工业出版社，2005.(Sun Yankui.Wavelet analysis and it’s application［M］.Beijing:China Machine Press，2005)

3Sweldens W.The lifiting scheme:A custom－design construction of biorthogonal wavelets［J］.App l Comput Harmon Anal.，1996，3:186－200.

4Sweldens W.The lifiting scheme:A construction of second generation wavelets［J］.SIAMJ Math Anal.，1997，29: 511－546.

5Daubech Ies I and Sweldensw.Factoring wavelet transforms into lifting steps［J］.J Fourier Anal Appl.，1998，4:247－269.

6Donoho D L.De-noising by soft threshold［J］.IEEE Trans.Info.Theory，1993，43:933－936.

DENOISING METHOD FOR SINGLE EPOCH GPS DEFORMATION MONITORING SIGNAL BASED ON LIFTING WAVELET

Tao Tingye，Gao Fei and Wu Zhaofu
(School of Civil and Hydraulic Engineering，Hefei University of Technology，Hefei230009)

P207

A

1671-5942(2011)03-0127-04

2010-11-21

国土环境与灾害监测国家测绘局重点实验室开放基金(LEDM2010B08);合肥工业大学博士学位专项基金(2010HGBZ0564)

陶庭叶，男，1980年生，讲师、博士，主要研究方向为GNSS定位技术与变形监测.E－mail:czytty@163.com