一种整周模糊度快速求解的分组搜索法*

晏红波 任超 卢献健

(桂林理工大学土木与建筑工程学院，桂林541004)

一种整周模糊度快速求解的分组搜索法*

晏红波 任超 卢献健

(桂林理工大学土木与建筑工程学院，桂林541004)

针对实际工作中观测条件较差的GPS卫星整周模糊度难以固定的问题，提出了模糊度快速求解的分组搜索法。首先将模糊度分为主模糊度和从模糊度两组，然后在固定主模糊度组的基础上，考虑从模糊度组能否固定。利用实际算例验证了该方法的有效性。

整周模糊度;快速求解;分组搜索;主模糊度;从模糊度

AbstractAn ambiguity group-searching method is brought forward.At first，decomposing the ambiguities into two groups according to their variance can reduce the influence caused by the low precision floats and minimize the searching space efficiently.Moreover，a new verification by comparing the search output is used in ambiguity validation.The results of the experiments indicate that the new method can efficiently reduce searching space，increase searching speed and enhance the success rate of ambiguity resolution.

Key words:integer ambiguity;quickly solving;group－searching;main ambiguity;slave ambiguity

1 引言

整周模糊度的求解是GPS高精度定位的核心问题。快速有效地解算整周模糊度对缩短野外观测时间、提高工作效率及拓展高精度动态定位应用的新领域，都极其重要［1，2］。目前，已经提出了多种模糊度快速解算方法［3－6］，但这些方法也存在一些不足:1)要求模糊度组全部固定。而在实际的GPS定位中，某些卫星由于各种因素的影响，观测质量不佳，模糊度难以固定，如果强行固定，解的质量不但不会提高，反而可能降低;2)模糊度搜索时，候选参数过多，搜索空间过大。

为解决以上问题，本文提出了模糊度分组搜索算法。考虑反映卫星信号质量的主要因素为方差，因此根据模糊度浮点解方差的大小，将其分为主模糊度(卫星观测质量较好)和从模糊度(卫星观测质量较差)两组，在固定主模糊度组的基础上，给定限定条件来决定是否固定从模糊度组，解决了模糊度的完全固定问题。同时，由于只搜索主模糊度组，候选参数和搜索空间都大为减小，可以有效提高搜索效率。

2 模糊度分组搜索算法

2.1 模糊度分组

设线性化后的观测方程为其中V为观测值残差，X、N分别为待定的基线和整周模糊度向量，A、B为其设计矩阵。组成法方程，可解得整周模糊度的浮点解^N及其协方差矩阵Q^N。

模糊度固定时，需满足以下条件

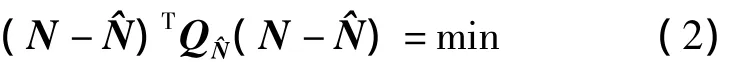
其N中是整周模糊度固定值。还可以表示成

式中QN^－1=LTDL，L是主对角元为1的下三角矩阵，D为对角阵。用χ2表示搜索范围，则式(3)化为:

从式(4)中可以看出，固定模糊度时为次序固定，即便进行了转换，如果其中有任一模糊度无法固定，则模糊度组整体无法固定［3］。而在实际工作中，由于观测条件的限制，在某些时刻往往有某颗或几颗卫星的观测质量不佳，使得其整周模糊度难以固定，此时无法获得固定解，影响动态定位效率。

模糊度搜索前，首先依据方差大小将模糊度分为两组。模糊度浮点解的方差-协方差矩阵Q是浮点解精度的反映，方差的大小反映了浮点解精度的高低。分组后得到:

其中，E表示方差较小的模糊度组(主模糊度)，F表示方差较大的模糊度组(从模糊度)。主模糊度的求解可以采用去相关和搜索的方法实现。对模糊度的搜索结果采用Ratio法和两次搜索比较法加以检验，检验通过则可以将其回代解算从模糊度F。

2.2 模糊度检验的两次搜索结果比较法分别为~N'［~n1'~n2'…~n'n－1~n'n］T，N~″［~n1″~n2″…~n″n－1~n″n］T。两次搜索比较具体做法是:将N~″与~N'进行比较，若~N″的每一元素与N~'中的对应相等，则接受N~″为主模糊度的固定解。当此条件不能满足主模糊度搜索结果的检验，采用Ratio法和两次搜索比较法相结合的方式:

1)对每一次搜索结果采用Ratio法对其进行检验，通过则接受其为正确解，否则返回重新分组搜索;

2)当连续两次分组搜索均不能通过Ratio检验时，则采用两次搜索比较法。

所谓两次搜索比较法，就是将两次未能通过Ratio检验的搜索结果加以比较，充分利用搜索结果信息，通过条件判断是否可以将其接受为固定解。设两次不同分组搜索得到的最小残差对应的两组解时，返回重新分组搜索。

采用两次搜索比较的方法，可以适当增大Ratio值，以保证解的可靠性。

2.3 从模糊度的计算

主模糊度搜索固定后，将其回代法方程，求解备选模糊度~F。备选模糊度~F的求解分为两步:

1)将~E回代法方程，求得备选模糊度^F';

2)对^F'进行条件判断，满足条件的固定为整数，否则保留浮点解。

对方程(1)，其法方程为:

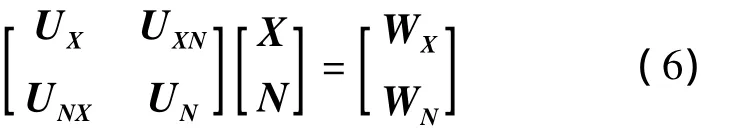
式中，U=［AB］TP［AB］，W=［AB］TPL，P为参数的权阵。

选定主模糊度后，法方程变为:

且行大于列，可以使用最小二乘法计算。设式(8)中左边第一项为¯U，右边项为¯W，取参数的权为Q= 1/Q，则式(8)的最小二乘解可表示为:

式中，^F'就是由主模糊度通过法方程计算得到的备选模糊度值。

由于整周模糊度具有整数特性，因此需要将^F'通过条件判断，进一步将其确定为整数。判定条件可以如下:

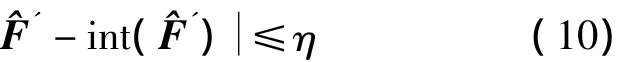
式中，int(·)表示取最近整数，η为指定的最大允许整周偏差，通常取0.1或0.15。

4 算例分析

4.1 分组搜索算法实际应用

为表明该方法提高了模糊度解算效率和成功率，在此仅列出其中一条基线作为算例(因篇幅有限)，以显示该方法的效果。

实验数据为30分钟静态短基线数据，基线长为1 633.139 3 m。在对该基线进行观测时，共有10颗可视卫星，因此在解算中组成9个双差整周模糊度。用bernese解算得到的模糊度固定解并将其视为真值。表1列出了模糊度解算时的浮点解及其方差，以及bernese解算的模糊度固定解。

表1 Bernese解算结果Tab.1Computation results from bernese solution

由表1看出，第2、3、5、6、7、8模糊度浮点方差较大，第1、4、9较小。解算时，首先进行模糊度的分组，将方差较小的模糊度选为主模糊度并搜索，对搜索结果的检验采用Ratio检验与两次搜索比较法。在此，本文列出了对此数据的两种不同分组情况的解算结果(表2)。

表2 两种分组情况下模糊度解算结果Tab.2Computed ambiguity rusults in two grouping cases

由表2可知，两组搜索结果均通过了Ratio检验，说明主模糊度搜索结果正确。将主模糊度回代方程(8)，则可以得到从模糊度的高精度实数解，通过条件判断(取η=0.1)，得到从模糊度的整数解。全部模糊度的固定解与真值完全一致。最后由全部模糊度的固定解求得基线分量的最终解。

另外，利用分组搜索法解算整周模糊度的时间比LAMBDA明显减少，表3是模糊度搜索耗时比较。因对单个的模糊度搜索CPU耗时不是很明显，所以表3中数据为搜索固定100次的耗时结果。

实验结果表明，模糊度搜索时，采用分组的方法，去掉方差较大的模糊度来实现搜索空间降维，对模糊度进行分组，只搜索部分模糊度，该方法不但能显著地提高模糊度的搜索效率，同时也能保证解的准确性。

表3 模糊度搜索耗时比较Tab.3Comparison between time-consuming of ambiguity Searching with different methods

4.2 两次搜索比较法的应用

实验中，模糊度搜索结果均能通过Ratio检验，本文提出的两次搜索法并未得到验证。为此，利用以下实验验证新检验方法的有效性。

以8772.849 0 m的基线为实验对象，该基线1小时观测数据的整周模糊度正确解为~N=［11 12］T。

对该基线的1～100、41～120历元进行解算，分别以不分组和分组(将第1、2、4模糊度选为主模糊度)的方式进行搜索，对模糊度有效性的检验取Ratio=2。此时，两种搜索方式均搜索到了正确解，但因为比例低而不能通过Ratio检验，模糊度的求解失败。但利用比较检验法则可以确定主模糊度搜索结果正确。新方法对两组数据的搜索结果如表4，对主模糊度的搜索结果见图1(图中❋与□分别表示未分组搜索最小与次小残差平方和对应的解;○与◇表示分组搜索最小与次小残差平方和对应的解)。

表4 模糊度搜索结果Tab.4Results of ambiguity searching

上述两组数据的单次搜索结果均不能通过Ratio检验。但通过比较发现，对每一组数据的两次搜索得到的最小残差平方和对应的模糊度解一致(图1(a)、(b)中圆与星号重叠)。此时接受［1 1 2］T为第1、2、4模糊度的正确解。将正确模糊度值回代求取从模糊度，最终全部模糊度的固定解为~N=［1 11 2］T，与模糊度的真值一致，全部模糊度解算成功。

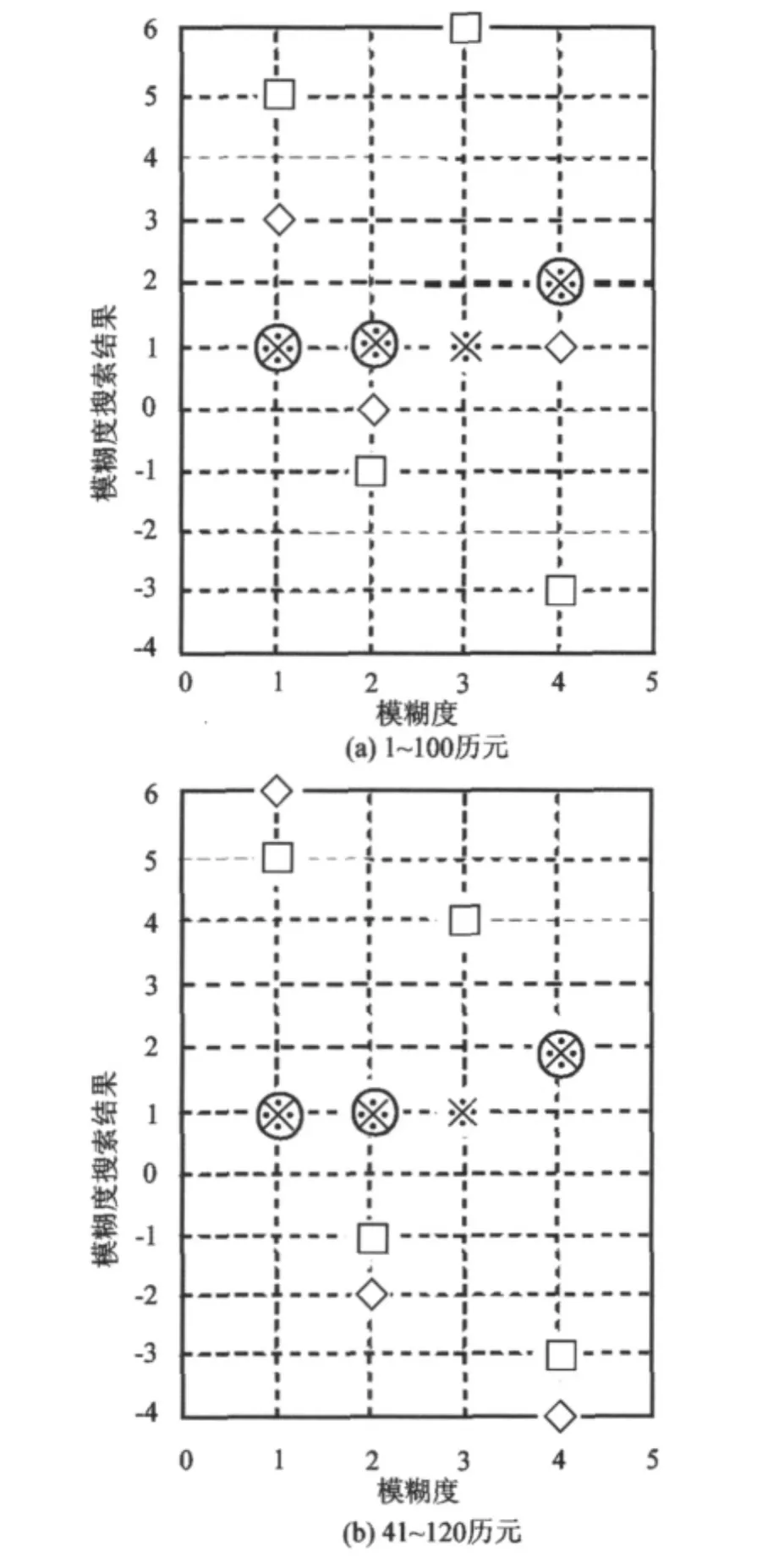
图1 两次搜索结果的比较Fig.1Comparison between the ambiguity searching results at two times

5 结论

采用分组方法实现搜索空间降维，减小搜索空间，有效地提高了模糊度的搜索效率，同时也能保证解的准确性。在观测质量较好的情况下，可以用独立模糊度搜索法(主模糊度数=3)来搜索固定模糊度，由此可以进一步提高搜索解算效率。

分组搜索法采用两次搜索比较检验法有效地减少了正确模糊度被拒绝的现象，而适当提高Ratio的取值，则可以降低接受错误解的概率。

值得注意的是，用分组搜索法解算模糊度时，充足的数据是准确解算模糊度的重要前提，当观测历元较少时，应尽量保证足够的主模糊度个数。

1阳仁贵，欧吉坤.提高GPS单频相位模糊度解算成功率的新方法［J］.南京航空航天大学学报，2005，37(3):280－283.(Yang Rengui and Ou Jikun.Method for improving success rate of phaseinteger ambiguity resolution of single frequency GPS receivers［J］.Journal of Nanjing University of Aeronautics＆Astronautics，2005，37(3):280－283)

2任超.GPS高精度动态定位理论及其在有轨载体定位中的应用［D］.中国科学院测量与地球物理研究所，2004.(Ren Chao.Research on the theories of precise kinematic GPS positioning and its application in rail-based vehicles［D］.Institute of Geodesy and Geophysics of Chinese Academy of Sciences，2004)

3Teunissen P J G.Precision volume and eigenspectra for GPS ambiguity estimation based on the time-averaged satellite geometry［J］.Journal of Geodesy，1997，71:290－301.

4阳仁贵，欧吉坤，袁运斌.部分搜索法提高GPS相位模糊度解算的效率和成功率［J］.武汉大学学报(信息科学版)，2007，2:160－163.(Yang Rengui，Ou Jikun and Yuan Yunbin.Facilitating efficiency and success rate of resolving GPS phase ambiguity with parts search method［J］.Geomatics and Information Science of Wuhan University，2007，2: 160－163)

5Verhagen S.On the approximation of the integer leastsquares success rate:which lower or upper bound to use［J］.Journal of Global Positioning Systems，2003，2(2): 117－124.

6Verhagen S，Teunissen P J G and Dennis Odijk.Carrierphase ambiguity success rates for integrated GPS-Galileo satellite navigation［A］.Proceedings Space，Aeronautical and Navigational Electronics Symposium SANE2007［C］.The Institute of Electronics，Information and Communication Engineers(IEICE)，2007，107(2):139－144.

A RAPID INTEGER AMBIGUITY SOLUTION——GROUP-SEARCH METHOD

Yan Hongbo，Ren Chao and Lu Xianjian
(The Department of Civil and Construction Engineering，Guilin University of Technology，Guilin541004)

P207

A

1671-5942(2011)03-0094-04

2011-01-23

国家自然科学基金(40574002);广西自然科学基金(0640178)

晏红波，女，1983年生，助教，主要从事GPS数据处理方面的研究.E－mail:yanhb@glite.edu.cn